Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

864.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

720.66 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

4. СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Система дифференциальных уравнений вида

dx1

(t,x ,x

,...,x

);

f2(t,x1,x2

,...,xn);

(4.1)

....................................

(t,x ,x

,...,x

где x1,x2,...,xn неизвестные функции переменной t, называется нормальной системой.

Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно x1,x2,...,xn, то система дифференциальных уравнений называется линейной.

Одним из основных методов решения систем дифференциальных уравнений является метод исключения неизвестных функций, который сводит задачу решения данной системы к решению одного дифференциального уравнения с одной неизвестной функцией, при этом порядок этого дифференциального уравнения равен n при условии, что система уравнений имеет вид, приведенный выше.

Сущность метода продемонстрируем на примере решения системы двух дифференциальных уравнений с двумя неизвестными функциями.

Пример 34. Найти общее и частное решения системы дифференциальных уравнений


	dx	2x y;

dt		x(0) 1; y(0) 3.
dy
		x 2y;

Решение. Дифференцируем первое уравнение системы по переменной t:

d2x	2	dx	dy	.	(4.2)
dt2		dt	dt

Подставляем в уравнение (4.2) выражение dy из второго урав- dt

нения системы:

d2x	2	dx	x 2y.	(4.3)
dt2		dt

Выразим y из первого уравнения системы:

		y		dx	2x.	(4.4)

				dt
Подставим (4.4) вместо y в уравнение (4.3):
	d2x		dx		dx
		2			x 2	2x .
	dt2		dt
					dt

После очевидных преобразований получаем уравнение

d2x 4dx 3x 0. dt2 dt

Имеем однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Находим решение согласно методам, изложенным в подразделе 3.3. Составляем характеристическое уравнение 2 4 3 0; его корни есть 1 3; 2 1.

Следовательно, общим решением уравнения является функция

x(t) C e3t C		et.	(4.5)
1	2

Дифференцируем функцию (4.5) по переменной t:

dx	3C e3t C		et ;	(4.6)
	3C e3t C		et ;	(4.6)
dt	1	2
dt

подставляем в правую часть уравнения (4.4) выражения

иdx из (4.6) и находим y(t): dt

y(t) 3C1e3t C2et 2C1e3t 2C2et

или

y(t) C1e3t C2et .

Теперь можно записать общее решение системы:

x(t) C1e3t C2et;y(t) C1e3t C2et.

x(t) из (4.5)

(4.7)

Найдем частное решение системы, для этого подставим в общее решение (4.7) начальные условия:

C		C		1;
	1		2	C1 2;C2 1.
	C C		2	3
	1		2

Подставляя найденные значения произвольных постоянных в общее решение (4.7), получаем частное решение системы:

x(t) 2e3t	et;
	et.
y(t) 2e3t	et.

Пример 35. Найти общее решение системы дифференциальных

	dx		2x y cost,

dt
уравнений		dy
				x 2sint.
		dt

Решение. Дифференцируем первое уравнение системы по переменной t:

d2x

sint.

(4.8)

dt2

Подставим в уравнение (4.8)

вместо

правую часть второго

уравнения системы, получим уравнение

d2x

x 2sint sint

dt2

или

d2x

x sint.

dt2

Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решаем уравнение согласно методам, изложенным в подразделе 3.3: общее решение ищем в виде

x(t) x(t) x (t),

где x(t) общее решение однородного уравнения, соответствующего неоднородному уравнению; x (t) частное решение неоднородного уравнения.

Сначала решаем однородное уравнение, соответствующее данному неоднородному.

	Для однородного уравнения			d2x		2	dx	x 0	составляем ха-
	Для однородного уравнения			dt	2	2	dt	x 0	составляем ха-
				dt	2		dt
рактеристическое уравнение 2 2 1 0							, его корни			1, тогда
									1,2
x	(t) C et C		tet общее решение однородного уравнения. Частное
1		2

решение ищем в виде x (t) Acost Bsint. Методом неопределенных коэффициентов найдем коэффициенты A и B. Для этого дважды

продифференцируем частное решение по t и подставим (x ) ,(x ) в неоднородное уравнение:

(x
	) Asint Bcost ;(x	) Acost Bsint;
Acost Bsint 2Asint 2Bcost Acost Bsint sint;
2Bcost 2Asint sint;

тогда B 0; A 1. Подставим найденные значения коэффициентов в

формулу общего вида частного решения, получим x (t) 1cost. Сле-

довательно, общее решение неоднородного уравнения есть функция

x(t) C et C

tet

cost .

(4.9)

y(t). Для

Теперь найдем

этого

сначала продифференцируем

функцию (4.9) по переменной t:

C et C

et C

tet

sint.

(4.10)

Из первого уравнения системы находим y:

2x cost .

(4.11)

Заменяя в формуле (4.11) x(t)и

на их выражения из формул

(4.11) и (4.10) соответственно, получаем после приведения подобных членов функцию

y(t) et C

(1 t) C 2cost

sint .

(4.12)

Формулы (4.9) и (4.12) дают решение системы дифференциаль-

ных уравнений:

x(t) et (C

cost;

y(t) et C

(1 t) C 2cost

sint.

Решить системы уравнений.

y 0;

4.1.

3x y.

x (t) x y et;

y (t) x y et.

5dx 2dy 4x y e t;dt dt

dx 8x 3y 5e t.4.3.

Вопросы к разделу « Системы линейных дифференциальных уравнений»

1.Укажите вид нормальной системы дифференциальных урав-

нений.

2.Какой метод решения нормальной системы дифференциальных уравнений вы можете указать?

5.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ВПРИЛОЖЕНИЯХ

Рассмотренные в предыдущих разделах пособия типы дифференциальных уравнений и методы их решения находят широкое применение при решении различных задач физики, теоретической механики, сопротивления материалов, строительной механики, экономики, биологии. По сути, дифференциальные уравнения являются математическими моделями реальных процессов и явлений, которые встречаются в инженерных задачах. Далее приведем примеры постановки и решения таких задач.

Пример 36. Материальная точка движется с постоянным ускорением a. Начальная скорость точки v0. Найти закон движения точки.

Решение. По определению,

dv a, dt

откуда

dv adt.

Интегрируя это дифференциальное уравнение, получаем общее решение

v at C1.

(5.1)

По условию, необходимо решить задачу Коши со следующими

данными: при t 0 (в начальный момент)	v v0 . Подставляя началь-
ные данные в общее решение (5.1), имеем
v0 0 C1, или C1	v0 .
Таким образом, уравнение (5.1) принимает вид
v at v0 .	(5.2)
Уравнение (5.2) представляет закон движения в виде v f (t).

Так как v dS , то решение задачи Коши (5.2) можно преобразовать к dt

виду

	dS		at v ,
			at v ,
	dt			0
или
dS atdt v0dt.							(5.3)
Интегрируя равенство (5.3), получаем общее решение задачи:
S			1	at2 v t C	2	.	(5.4)
S				at2 v t C		.	(5.4)
		2		0
		2

Для определения постоянной интегрирования C2 используем начальные условия: при t=0 S S0 . Подставляя эти значения в равенство (5.4), получаем

S0 0 0 C2,

или C2=S0. Таким образом, уравнение движения (5.4) принимает вид

S	1	at2	v t S	0	.		(5.5)

2			0

Это уравнение представляет искомый закон движения в виде
S f (t).			положить a g;
Если в уравнениях (5.2) и (5.5)						v0 0;	S0 0;

Sh,то получаем закон свободного падения тела в пустоте:

vgt; h 1 gt2 .

В разделе 4 пособия была рассмотрена нормальная система дифференциальных уравнений (4.1). С механической точки зрения эта система задает поле скоростей движений, где t – время; x1,x2,...,xn прямоугольные координаты точки фазового пространства.

Решение системы есть функции

x1 1(t,t0,x10,x20,...,xn0);

........................................ (5.6)

xn n(t,t0,x10,x20,...,xn0),

определяющие в любой момент времени t положение движущейся точки, которая в начальный момент времени t0 занимала положение

(x10,x20,...,xn0). При такой интерпретации система (4.1) называется динамической, а каждое ее решение (5.6) – движением. Кривая, описываемая точкой при движении, называется траекторией движения.

Уравнения (5.6) задают траекторию движения в параметрическом виде, t – параметр. Отметим, что при n = 2 имеем движение в плоскости (x1,x2), при n = 3 имеем движение в пространстве

(x1,x2,x3).

В общем случае в дифференциальные системы уравнений могут входить производные высших порядков. В этом случае получается система дифференциальных уравнений высших порядков.

Пример 37. Задача о движении материальной точки под действием силы F, рассматриваемая в теоретической механике, сводится к системе трех дифференциальных уравнений второго порядка. Обозначим через Fx,Fy,Fz проекции силы F на оси координат. Положе-

ние точки в любой момент времени t определяется ее координатами x, y, z, которые являются функциями от времени t; проекции вектора

скорости на оси координат есть dx,dy ,dz (в теоретической механике dt dt dt

их обычно обозначают через x, y,z).

Пусть сила F (а следовательно, и ее проекции) зависит от времени t, положения x, y,z точки и скорости движения точки. Тогда математической моделью поступательного движения материальной точки массы m, согласно закону Ньютона, является система трех дифференциальных уравнений второго порядка:

d2x

(t,x, y,z,

);

dt2

d2 y

(t,x, y,z,

);

(5.7)

dt2

d2z

F (t,x, y,z,

Решением этой системы являются функции x(t,C10,C20); y(t,C10,C20); z(t,C10,C20), которые дают траекторию движения точки в пространстве R3, константы C10,C20 определяются из начальных условий.

Очевидно, что в случае плоского движения, когда траекторией является кривая в плоскости XOY, имеем систему


mx	Fx(t,x, y,x, y);	(5.8)
		(5.8)
my	Fy(t,x, y,x, y).

Заметим, что решать систему дифференциальных уравнений высших порядков можно путем сведения ее к системе дифференциальных уравнений первого порядка или в некоторых конкретных случаях используя искусственные приемы.

Получим систему вида (5.8) для решения конкретной задачи: тело брошено под углом к горизонту и движется в среде, сопротивление которой пропорционально скорости v тела; найти траекторию движения.

Решение. В любой точке M(x, y) траектории на тело действуют две силы: тяжести P mg и сопротивления среды F kv(рис. 1).

F M(x,y)

Рис. 1

Найдем проекции на оси координат равнодействующей этих сил

Fp :

				^	OX);
Fpx		Pcos(P,	OX) F cos(F,
					(5.9)

	Fpy	Pcos(P,	OY) F cos(F,		OY).

Так как cos(P, OX) 0; cos(F, OX) dx ; ds

cos(F, OY) dy , система (5.9) принимает вид ds

;Fpx kv

	ds
Fpy	mg kv	dy	.

		ds

cos(P, OY) 1;

(5.10)

Поскольку v ds , то систему (5.10) можно записать в виде dt

;Fpx k

		dy	dt
Fpy	k		mg.

		dt

Тогда, согласно второму закону Ньютона [см. формулу (5.8)], имеем дифференциальные уравнения движения

	mx kx;
		(5.11)
my ky		mg.

Каждое из дифференциальных уравнений, входящих в систему (5.11), содержит только одну неизвестную функцию, поэтому интегрирование системы сводится к интегрированию по отдельности каждого из уравнений системы. Первое уравнение системы есть линейное однородное дифференциальное уравнение с постоянными коэффициентами, второе – линейное неоднородное дифференциальное уравнение с постоянными коэффициентами. Уравнения такого типа были рассмотрены в подразделе 3.3, поэтому приводим решение уравнений

системы (5.11) без особых комментариев.

d2x

0, следова-

dt2

тельно, общее решение уравнения ищем в виде

x C1x1

C2x2; со-

ставляем характеристическое уравнение:

m 2 k 0 (m k) 0 0;

x 1;x

e m .

Тогда функция x C C

есть

общее решение первого

e m

уравнения системы (5.11).

Решаем второе уравнение системы (5.11):

d2 y

k dy

dt2

m dt

y ;

ищем в виде y

e m

;

Общее решение уравнения

y At;(y ) A;(y ) 0.

Подставляем в уравнение y ,(y ) ,(y ) и находим значение A:

	k	A g A	gm	; следовательно,	y	gm	t; общее решение
	m	A g A		; следовательно,	y		t; общее решение
	m		k			k
								k	t
									t
второго уравнения системы (5.11) есть функция y C3 C4e m

gmt. Таким образом, получили общее решение системы (5.11): k

					k	t
	x(t) C C					t		;
	x(t) C C		e m					;
	1	2							(5.12)
		k					gm		(5.12)
				t					t.
				t
		m
y(t) C3 C4e								k
								k

Найдем частное решение системы (5.11), используя начальные условия: x(0) 0; y(0) 0;x (0) v0 cos ; y (0) v0 sin .

Подставим первые два из начальных условий в общее решение (5.12), получим систему

0 C1 C2;

(5.13)

0 C3 C4.

Из системы (5.12) имеем, дифференцируя оба уравнения систе-

мы:

dx k C2e m ;

dt m t

			k
dy	k			t	gm

		C4e m				.
	m
dt					k

Тогда, используя два последних равенства из начальных условий, получаем

	v0 cos			k	C2;

				m
		k			(5.14)
v0 sin			C4			gm	.
		m
						k

Из систем (5.13) и (5.14) находим произвольные постоянные:

cos ; C

(gm kv sin );

(gm kv sin ).

Подставляя найденные значения C1, C2 , C3, C4 в общее решение (5.12), получаем частное решение системы:

x(t)

cos (1 e m

);

k 0

(5.15)

y(t)

(gm kv

sin )(1 e

t )

Система (5.15) есть уравнения движения (траектория движения) камня в параметрическом виде. При желании можно исключить параметр t и получить траекторию движения в виде уравнения y f (x).

В подразделе 3.3 были рассмотрены линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Применительно к задачам, рассматриваемым в курсе теоретической механики, такие уравнения обычно записывают в виде

x px qx 0.

(5.16)

Тогда в зависимости от вида корней характеристического уравнения находим общее решение, а при наличии начальных условий и частное решение дифференциального уравнения (см. примеры 20–23).

Для случая действительных и различных корней характеристического уравнения уравнение вида x qx 0встречается при рассмотрении движения материальной точки под действием центральной отталкивающей силы и при исследовании относительного движения точки в случае переносного вращательного движения.

Равные действительные корни характеристического уравнения при решении уравнения вида (5.16) встречаем при исследовании апериодического прямолинейного движения точки, происходящего под действием восстанавливающей упругой силы, зависящей от координат точки, при сопротивлении среды, пропорциональном скорости точки.

Уравнения вида (5.16), для которых характеристическое уравнение имеет комплексно-сопряженные корни, встречаются при исследовании свободных колебаний материальной точки под действием восстанавливающей силы, пропорциональной координате точки; рассмотрении относительного движения точки; решении задач, связан-

ных с движением материальной точки под действием центральной силы; исследовании колебаний циклоидального маятника; рассмотрении малых колебаний математического и физического маятников.

Пусть теперь имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

x px qx f (t).

(5.17)

Дифференциальное уравнение (5.17) в случае, если корни характеристического уравнения соответствующего ему однородного уравнения комплексно-сопряженные, а правая часть есть линейная функция от косинуса и синуса (см. случай 3 для правой части специального вида, рассмотренный в подразделе 3.3, а также примеры 30, 31), встречается при исследовании вынужденных колебаний материальной точки в ситуации, когда восстанавливающая сила пропорциональна координате точки, а сопротивление пропорционально скорости точки, а также при исследовании относительного движения точки.

Частный случай уравнения (5.17) вида x qx f (t) при указанных выше условиях встречается при исследовании колебаний материальной точки, если на точку действуют восстанавливающая сила, пропорциональная координате точки, и возмущающая сила, изменяющаяся по гармоническому закону. Такое движение точки представляет собой результат наложения свободных и вынужденных колебаний точки. Решение однородного уравнения определяет свободные колебания, а частное решение неоднородного уравнения – вынужденные колебания точки.

Если возмущающая сила изменяется по экспоненциальному закону (имеем случай 2 для правой части неоднородного уравнения в подразделе 3.3), то дифференциальное уравнение (5.17) встречается при решении задач теоретической механики, связанных с колебаниями и апериодическим движением материальной точки.

Пример 38. Проводнику сообщен заряд 1000 Кл. Вследствие несовершенства изоляции проводник постепенно теряет свой заряд. Скорость потери заряда в данный момент пропорциональна имеющемуся заряду проводника. Какой заряд останется на проводнике через 10 мин, если за первую минуту потеряно 100 Кл?

Решение. Пусть в момент t заряд проводника стал равен Q. Ско-

рость потери заряда в этот момент равна dQ . По условию, эта ско- dt

рость пропорциональна заряду Q, следовательно, имеем дифференциальное уравнение

dQ kQ, dt

где k – коэффициент пропорциональности.

Это уравнение типа y f (y), т. е. уравнение с разделяющимися переменными. Разделяем переменные, получаем

dQ kdt. Q

Интегрируем обе части равенства, получаем общее решение уравнения

lnQ kt lnC,

или

Q Ce kt .
Используем начальные условия Q(0) Q0		для определения по-
стоянной интегрирования C:
Q Ce k 0	, или C Q .
0	0
Тогда частное решение уравнения принимает вид
Q Q e kt.		(5.18)
	0

Уравнение (5.18) дает величину Q в любой момент времени t. Поскольку, по условию, за первую минуту потеряно было 100 Кл, то

900=1000e k t , откуда e-k = 0,9. Подставляем это значение в равенство (5.18), получаем

Q 1000 0,9t.

Следовательно, через 10 мин заряд проводника составит

Q 1000 0,910Kл.

Пример 39. Конденсатор, емкость которого Q, включается в цепь с напряжением E и сопротивлением R. Определить величину заряда q конденсатора в момент t после включения.

Решение. В момент t заряд конденсатора равен q и сила тока i=

dq. К этому моменту времени в цепи действует электродвижущая dt

сила E, равная разности между напряжением цепи U и напряжением конденсатора q : E U q .

Q	Q
По закону Ома, сила тока i		E	, тогда	dq	U q/Q	. Следова-
				dt
		R			R

тельно, дифференциальное уравнение процесса имеет вид


	R	dq	U		q		.
		dt
					Q
Преобразуем его к виду
	dq		q	U		.		(5.19)
			QR
	dt				R

Имеем линейное дифференциальное уравнение первого порядка. Решим его методом вариации произвольной постоянной (см. подраздел 2.4, пример 8). Найдем общее решение однородного уравнения, соответствующего данному:

lnC CeQR .

dt QR

Общее решение неоднородного уравнения ищем в виде

(5.20)

q C(t)e QR .

Дифференцируем равенство (5.20):

C (t)e

C(t)

(5.21)

Подставляем q и q из формул (5.20) и (5.21) соответственно в

уравнение (5.19), получаем тождество

C(t)

C(t)eQR

C (t)e

из которого находим C (t), а затем и C(t):

C (t) U eQR C(t) UQ eQR C. R

Подставим найденное выражение для C(t) в формулу (5.20) и получим общее решение уравнения (5.19):

q(t) UQ CeQR .

Используем начальное условие q(0) 0 для определения произвольной постоянной C в общем решении: 0=UQ+C C UQ. Окончательно получаем уравнение, описывающее рассматриваемый процесс:

q(t) UQ(1 eQR .

Пример 40. В цепи с сопротивлением R и самоиндукцией L действует периодическая электродвижущая сила

E1 asin 2 t,

где T – период; t – время; a – постоянное число, равное максимальному значению величины E1.

Определить силу тока i в цепи в любой момент времени, если в начальный момент времени сила тока равна нулю.

Решение. В цепи действуют две силы: электродвижущая сила

E asin

t и противоположная ей электродвижущая сила индук-

ции E2

Общая электродвижущая сила

E E E

asin

t L

Так как по закону Ома сила тока в цепи i

, то

asin

t L

Преобразуя очевидным образом последнее равенство, получаем дифференциальное уравнение процесса:

L	di	Ri asin	2	t.	(5.22)
	dt
			T

Уравнение (5.22) является линейным неоднородным дифференциальным уравнение первого порядка (см. подраздел 2.4). Решим его методом Бернулли (см. пример 9).

Полагаем i u v, тогда i u v uv , подставляя эти равенства в уравнение (5.22), получаем (предварительно поделив обе части уравнения на L)

sin

u v uv

t u v

v 0

dt lnv

t v e L .

Тогда, подставляя найденное выражение для функции v в уравнение, получаем

sin

t u

sin t

u e

sin

tdt.

(5.23)

Интеграл в последнем равенстве вычисляем по формуле интегрирования по частям: udv uv vdu.

u eLt

eLtdt;

sin

tdt

sin

tdt

cos

Еще раз интегрируем

cos

eL cos

tdt

2 L

по частям

u eL

eL dt;

eL cos

cos

tdt v

sin

tdt

2 L

2 L 2

T2R

T2R2

cos

sin

tdt.

2 2 L2

2 2 L

Тогда после очевидных преобразований получаем равенство

T2R2

T2R

tdt

sin

cos

sin

2 e

(2 )

(2 )2 L2

T2R2

sin

tdt

( cos

sin

(2 )2 L2

2 L

2 TL2

sin

tdt

( cos

sin

t).

(2 )2 L2

T2R2

2 L

Подставим полученное выражение для интеграла в (5.23),

тогда

2 TLa

( cos

sin

t) C.

(2 )

2 L

Следовательно, общее решение уравнения (5.22) принимает вид

2 aTL

( cos

sin

t) Ce L .

(5.24)

(2 )

2 2

2 L

L T

Для определения постоянной интегрирования C используем начальное условие i(0) 0; подставим его в общее решение (5.24):

0	2 aTL					C C		2 aTL				.
0	(2 )	2 2	2	R	2	C C	(2 )	2 2	2	R	2	.
	(2 )	L T		R			(2 )	L T		R

Тогда искомое частное решение принимает вид

2 aTL

cos

sin

e L .

(2 )

2 2

2 L

(2 )

L T

После очевидных преобразований получаем

2 aTL

(2 )

sin

t cos

2 L

Пример 41. Тело брошено вертикально вверх с начальной скоростью v0. Найти закон движения тела, считая, что оно движется только под действием силы тяжести.

Решение. В общем виде закон движения есть S f (t). Определим функцию f (t). Согласно второму закону динамики,

m	d2S		F,	(5.25)
	dt	2

d2S

где ускорение движущегося тела; m его масса; F – сила, dt2

действующая на тело в направлении движения.

По условию задачи, сила F равна силе тяжести mg, которая направлена вниз, т. е. в сторону, противоположную движению, поэтому

F mg. (5.26)

Тогда из формул (5.25) и (5.26) имеем дифференциальное уравнение движения

d2S

dt2

g. (5.27)

Уравнение (5.27) есть уравнение вида y const. Уравнения такого типа были рассмотрены в подразделе 3.2. Последовательно дважды интегрируем уравнение (5.27), тогда имеем

dS	gt C ;	(5.28)

dt	1

ma mg kv2.

			S ( gt	C )dt	gt	2	C t C		2	.	(5.29)
			S ( gt	C )dt			C t C			.	(5.29)
				1	2	1
Определим произвольные постоянные C1								и C2 из начальных ус-
ловий:	S(0) 0; S (0) v0.			Подставляя первое начальное условие в
уравнение (5.29), а второе – в (5.28), получаем								C1 v0; C2 0.			Тогда
S v0t		gt2
			.
		2	.
		2

Пример 42. Тело массой m падает с некоторой высоты со скоростью v. При падении тело испытывает сопротивление, пропорциональное квадрату скорости. Найти закон движения падающего тела.

Решение. В момент t тело находится под действием тяжести и сопротивления среды. Сила тяжести равна mg; сила сопротивления

среды, согласно условию, равна kv2и направлена в сторону, противоположную движению тела. Тогда равнодействующая этих сил равна

mg kv2. C другой стороны, сила, действующая на тело, согласно первому закону динамики, равна ma, a – ускорение движения. Таким образом, имеем равенство

(5.30)

Так как скорость v S (t), а ускорение при прямолинейном движении a S (t), где S – путь, пройденный телом от начала отсчета, то равенство (5.30) принимает вид

	d2S		dS		2
m			mg k		.	(5.31)
	dt	2
				dt

Уравнение (5.31) есть дифференциальное уравнение второго порядка, допускающее понижение порядка (см. подраздел 3.2).

Поскольку

v, то

d2S

Тогда уравнение

dt2

(5.31) принимает вид

mg kv2.

(5.32)

С формально-математической точки зрения здесь за новую независимую переменную берем S [поскольку независимая переменная t не входит в уравнение (5.31)], а за функцию – v(S).

Уравнение (5.32) есть дифференциальное уравнение первого порядка с разделяющимися переменными; разделяя переменные, получаем

mvdv

mg kv2

C S.

(5.33)

Определим постоянную C, приняв, что в начальный момент

времени t=0 пройденный путь S=0,

тело начало падать с начальной

скоростью v v(0) 0. Тогда из равенства (5.33) получаем

lnmg C 0 C

lnmg.

Находим частное решение уравнения (5.32):

mg kv

lnmg S

или

S =

mg kv2

Возвращаясь к первоначальной независимой переменной t и ис-

комой функции S(t), получаем (учитывая, что

2kS

mg S (t)

Тело падает, поэтому S (t)>0 и, следовательно, из формулы

(5.31) имеем

2kS

>0, тогда

. Найдем из последнего

dS 2

mg k(S (t))

mg k

равенства

2kS

(1 e

Учитывая, что функция S(t) возрастающая,

>0, поэтому

2kS

1 e

(5.34)

Равенство (5.34) есть дифференциальное уравнение с разделяющимися переменными, тогда, разделяя переменные, получаем

t C.

2kS

1 e

Вычислим интеграл в последнем равенстве.

2kS

1 e m

mdz

em z

em dS dz dS

kem

zdz

z2 1

k z

z2 1

z2 1 k

2kS

Тогда имеем общий интеграл уравнения (5.34)

2kS

t C.

(5.35)

Подставим в общий интеграл (5.35) начальное условие S(0) 0, получим C 0, частный интеграл уравнения (5.34) принимает вид

2kS

или, потенцируя, получаем

	kS			2kS		kg	t
em			e m 1 e			m .		(5.36)

Чтобы получить закон движения, т. е. функцию S(t) в явном виде, сделаем некоторые преобразования. Из равенства (5.36) следует

1			kg	t

		e	m .

kS	2kS

em e m 1

Умножая числитель и знаменатель левой части последнего ра-

kS 2kS

венства на em e m 1, получаем

2kS

e m

1 e

m .

(5.37)

Складываем равенства (5.36) и (5.37), получаем

m ).

(5.38)

Логарифмируем выражение (5.38), получаем закон движения падающего тела

			t	kg		kg	t
	m
S(t)			e	m	e	m
		ln						.
	k				2

Наряду с задачей Коши для дифференциальных уравнений высших порядков представляют большой интерес краевые задачи, в которых условия, налагаемые на искомое решение, задаются не в одной точке, а на концах некоторого отрезка a,b и ищется решение, определенное внутри этого отрезка. Эти условия называются краевыми условиями и состоят в том, что на обоих концах отрезка a,b задаются значения искомого решения или значения производных от искомого решения, или, в общем случае, линейная комбинация ординат и производных решения.

Задача нахождения решения дифференциального уравнения, удовлетворяющего заданным краевым условиям, называется краевой задачей. Краевые задачи возможны для дифференциальных уравнений второго и высших порядков.

Вобщей теории обыкновенных дифференциальных уравнений высшего порядка линейные уравнения занимают особое место. Это объясняется разработанной теоретической базой решения таких уравнений и многочисленными приложениями в технике и физике.

Краевая задача называется линейной, если дифференциальное уравнение и краевые условия линейны.

Вобщем виде линейная краевая задача для обыкновенного дифференциального уравнения второго порядка имеет вид

y p(x)y q(x)y f (x);		(5.39)
	0 y(a) 1y (a) A;	(5.40)
		(5.40)

0 y(b) 1y (b) B,

где функции p(x),q(x), f (x) непрерывны на [a,b];

0 1 0; 0 1 0.

Требуется найти функцию y y(x), дважды дифференцируемую на [a, b] и удовлетворяющую дифференциальному уравнению (5.39) и краевым условиям (5.40).

Линейная краевая задача (5.39), (5.40) называется однородной,

если f (x) 0 и A=0; B=0, т. е. когда дифференциальное уравнение и краевые условия однородны. В противном случае линейная краевая задача называется неоднородной.

Многие задачи сопротивления материалов, строительной механики, гидродинамики сводятся к решению краевых задач для обыкновенных дифференциальных уравнений.

Пример 43. Рассмотрим задачу о продольно-поперечном изгибе стержня. Имеется стержень переменного сечения. Расположим его

вдоль оси ОХ.
вдоль оси ОХ.				q=q(x)
Пусть y(x) величии-				q=q(x)
Пусть y(x) величии-
на прогиба точки	x оси
стержня под действием наг-
рузки с интенсивностью q(x)						P
и продольной силы P const		0


(рис. 2).						X
(рис. 2).					l	X
Тогда основное уравне-					l



ние имеет вид	(5.41)		Y
EI(x)y (x) M(x),	(5.41)				Рис. 2

где E – модуль упругости материала; I(x) момент инерции в сечении x; M(x) изгибающий момент в сечении стержня.

При статически определимых условиях (например, свободное опирание) моменты подсчитываются:

			M(x) Py(x) M1(x),		(5.42)
где M1(x) момент от поперечной нагрузки.
Из формул (5.41), (5.42) следует равенство
		EI(x)y (x) Py(x) M1(x).
После очевидных преобразований получаем
					(5.43)
		y (x) p(x)y(x) f (x),
где p(x)	P	; f (x)	M1(x)	.
	EI(x)
			EI(x)

Для определения однозначного решения уравнения (5.43) необходимо наложить граничные (краевые) условия. Для случая свободного опирания имеем

y(0) 0; y(l) 0. (5.44)

Уравнение (5.43) вместе с краевыми условиями (5.44) составляет краевую задачу.

Пример 44. Рассмотрим задачу об изгибе горизонтальной балки, лежащей на двух опорах x 0; x l, под действием распределенной поперечной нагрузки с интенсивностью q(x) (рис. 3). Известно (из

курса сопротивления материалов), что вертикальный прогиб балки приближенно удовлетворяет дифференциальному уравнению

	l
	l		q(x),	(5.45)
		EI(x)y	q(x),	(5.45)
		где E – модуль упругости
Y		где E – модуль упругости
Y	Рис. 3	материала балки;I(x) мо-

мент инерции поперечного сечения в точке x относительно горизонтальной прямой, лежащей в плоскости этого сечения и проходящей через центр его тяжести.

Отметим, что EI(x) жесткость балки при изгибе; изгибающий

момент M(x) EI(x) d2 y ; поперечная сила Q(x) M (x) EI(x)y . dx2

Если жесткость балки постоянна, то уравнение (5.45) принимает

вид

d4 y

EI q(x). (5.46) dx4

Общее решение уравнения (5.45) или (5.46) содержит четыре произвольных постоянных, которые можно определить, задав краевые условия. Краевые условия зависят от способа заделки концов балки.

Основные случаи:

1. Конец свободен. Тогда изгибающий момент и поперечная сила равны нулю, т. е. для свободного конца балки y 0; y 0. Таким образом, если оба конца балки свободны, то y (0) y (l) 0; y (0) y (l) 0.

2. Конец шарнирно оперт. Тогда нулю равны прогиб балки y и изгибающий момент M. Поэтому краевые условия для шарнирно опертого конца y 0; y 0. Следовательно, если оба конца шарнир-

но оперты, то y(0) y(l) 0; y (0) y (l) 0.

3. Конец жестко заделан. Тогда нулю равны прогиб y и угол по-

ворота arctgy и краевые условия	принимают вид y 0; y 0.
Если оба конца жестко заделаны, то	y(0) y(l) 0; y (0) y (l) 0.

Возможны и другие более сложные случаи. Уравнение (5.45) [или (5.46)] вместе с условиями 1, или 2, или 3 составляют краевую задачу.

Пример 45. Найти максимальный прогиб консольной балки длиной l, нагруженной равномерно распределенной нагрузкой q (рис. 4).

Решение. Дифференциальное уравнение изгиба балки [см. урав-

нение (5.46)]

d4 y

q. Интегрируем это уравнение последователь-

dx4

но четыре раза: EI

d3y

qx C

q(x)

dx3

d2 y

C x C

dx2

EI dy qx

C x

C x C

EIy

qx4

C3x C4.

Рис. 4

Таким образом, имеем общее решение уравнения (5.46). Для определения произвольных постоянных используем краевые условия. Левый конец балки жестко заделан, поэтому y(0) 0; y (0) 0, следовательно, C3 0;C4 0. Так как правый конец балки свободен, то y (l) 0; y (l) 0. Следовательно, 0 ql C1 C1 ql;

0 0,5l2 ql2 C2 C2 0,5ql2.

Подставляя найденные значения C1,C2, C3,C4 в общее решение, получаем решение краевой задачи (частный интеграл)

EIy 1 qx4 1qlx3 1 ql2x2,

24 6 4

или частное решение

y	q	x	2	(x	2	4lx 6l	2	).
y	24EI	x		(x		4lx 6l		).
	24EI

Это решение позволяет получить величину прогиба балки дляx 0,l . Очевидно, балка имеет максимальный прогиб на конце при

x=l, равный y(l) ql4 . 8EI

Пример 46. Рассмотрим задачу об изгибе балки на упругом основании. Балка переменного сечения длиной l лежит на упругом основании, оказывающем сопротивление вертикальным смещениям каж-

q(x)

дой точки балки. Коэффициент по-

q(x)

датливости основания k(x) задан.

y(x) прогиб балки в сечении x (в

вертикальном направлении), нача-

ло координат совмещено с левым

XX концом балки (рис. 5).

Рис.5

Рис. 5

Уравнение, описывающее прогиб балки, имеет вид

(EI(x)

d2 y

) k(x)y q(x),

(5.47)

dx2

где q(x) интенсивность нормальной нагрузки.

К уравнению (5.47) необходимо добавить граничные условия, по два на каждом конце. Например, если концы балки шарнирные, то

y(0) y(l) 0; y (0) y (l) 0.

(5.48)

Уравнение (5.47) и граничные условия [например, (5.48)] составляют линейную краевую задачу.

С краевой задачей тесно связана задача о собственных значениях. Однородная краевая задача имеет всегда нулевое (тривиальное) решение y(x) 0, которое с практической точки зрения не представляет интереса. Поэтому рассматривают ненулевые решения однородной краевой задачи, которые существуют не всегда. В связи с этим в дифференциальное уравнение или в краевые условия вводится параметр , варьируя который, можно добиться, чтобы при некоторых его значениях соответствующая краевая задача имела ненулевые решения.

Эти значения параметра k называются собственными зна-

чениями или характеристическими числами задачи, а соответствующие им ненулевые решения yk (x) собственными (характеристиче-

скими) функциями задачи. В результате имеем задачу нового типа – задачу о собственных значениях. Многие линейные однородные краевые задачи, встречающиеся в физических приложениях, включают параметр и имеют вид

y p(x)y q(x)y y 0;

0 y(a) 1y (a) 0;0 y(b) 1y (b) 0,

где не зависящий от x параметр, остальные функции определены в пояснениях к формулам (5.39), (5.40).

Нулевые решения y 0 существуют для всех значений параметра , кроме того, возможно, что для некоторых значений параметра существуют ненулевые решения.

Пример 47. Исследовать краевую задачу

y y 0;	(5.49)
y(0) 0; y(l) 0.	(5.50)

Решение. Исследовать краевую задачу означает найти такие значения параметра , при которых существуют нетривиальные (ненулевые) решения уравнения (5.49), удовлетворяющие краевым условиям (5.50), т. е. требуется найти собственные значения и собственные функции краевой задачи (5.49), (5.50).

Возможны три случая: 0; 0; 0.

1. 0.

Решаем уравнение y y 0. Уравнения такого типа были рассмотрены в подразделе 3.3 (примеры 20 23), поэтому решение приводим без дополнительных пояснений.

k2 0 k

;

общее решение y(x) C e x C

1,2

Для краевых условий (5.50) имеем систему уравнений

С1 С2 0;

Так как

0, C1 0;C2

C e

l C

Тогда y(x) 0.

2. 0.

(x) C2

y(x) C2x C1.

В полученное

общее

y (x) 0 y

решение подставляем краевые условия (5.50):

	С 0;	C 0;	Следовательно, y(x) 0.
	1	1	Следовательно, y(x) 0.
C2l C1 0		C2 0.
3. 0.				2

		0. Тогда	k		k1,2	i.	Следовательно,
y	(x) y(x)	0. Тогда	k		k1,2	i.	Следовательно,

общее решение дифференциального уравнения есть функция

y(x) C1 cos x C2 sin x.

Так как краевые условия (5.50) должны удовлетворять этому решению, то имеем систему уравнений

С1 1 С2 0 0;

	l C2 sin	l 0
C1 cos

Будем считать, что C2 0, иначе

Тогда sin l 0 l k

C1 0;

C2 sin l 0.

y(x) 0.

k , k 1,2,....

Таким образом, ненулевые решения задачи (5.49), (5.50) возможны, если

k	( k)2	, k 1,2,3,...
	l2
Этим собственным	значениям соответствуют собственные
функции

yk (x) sin kx, k 1,2,3,....

Пример 48. Найти собственные значения и собственные функции для краевой задачи: y 2 y 0; y(0) 0; y (l) 0.

Решение. Характеристическое уравнение имеет вид r2 2 0, тогда r1,2 i и общее решение дифференциального уравнения есть функция

y(x) C1 cos x C2 sin x;следовательно,y (x) C1 sin x C2 cos x.

Подставляя в y(x) и y (x)		краевые условия, получаем систему урав-
нений, из которой определим C1,C2 :
	C1 C2 0 0;				С1 0;
					cos l 0.
C1 sin l C2 cos l 0				C2
Считаем, что C2 0		[иначе y(x) 0], тогда (принимая C2 1)
cos l 0 cos l 0 l			k l			(1 2k), k 0,1,2,...

		2			2

Таким образом, нетривиальные (ненулевые) решения краевой

задачи возможны, если

k (2k 1) ; k 0,1,2,...

Собственным значениям k соответствуют собственные функ-

ции

yk (x) sin (2k 1) ; k 0,1,2,...

Пример 49. Найти минимальное значение силы Pкр (критиче-

ской силы), при котором происходит продольный изгиб стержня постоянной жесткости EI под действием сжимающей силы P, направленной вдоль оси стержня. Левый конец стержня (x=0) заделан, а правый (x=l) оперт.

Решение. Из курса сопротивления материалов известно, что величина отклонения стержня от его оси y y(x) удовлетворяет дифференциальному уравнению

y(4)	P	y 0,	(5.51)

где P – параметр.	EI

В соответствии с условиями на концах стержня выполняются
краевые условия (случаи 2 и 3):
y(0) y (0) 0; y(l) y (l) 0.			(5.52)

С математической точки зрения вопрос сводится к определению наименьшего положительного значения параметра P, при котором линейная однородная краевая задача (5.51), (5.52) имеет ненулевое решение.

Найдем общее решение уравнения (5.51). Это линейное однородное уравнение четвертого порядка. Уравнения такого типа были рассмотрены в подразделе 3.3 (примеры 25, 26, 27). Согласно алгоритму, составляем характеристическое уравнение и находим его корни:

k2 0 k2(k2

) 0 k

0; k

3,4

1,2

Следовательно, общее решение уравнения имеет вид

y(x) C1 C2x C3 cos x C4 sin x;

(5.53)

(5.54)

Продифференцируем равенство (5.53):

y (x) C2

C3 sin x C4 cos x.

(5.55)

Подставляя первые два краевых условия (5.52) в (5.53) и (5.55),

имеем

С1 C3 0;

C ;C

C2 C4 0

Тогда общее решение (5.53) можно записать в виде

y(x) C C

x C cos x

sin x

или

sin x

y(x) C (1 cos x) C

(5.56)

Дважды дифференцируя функцию (5.56), получаем

cos x C2 sin x.

(5.57)

(x) C1

Подставляем краевые условия (5.52) для правого конца стержня

в функции (5.56), (5.57), получаем систему уравнений

sin l

С1

(1 cos l) C2(l

) 0;

sin l

C cos l C

Эта система линейных однородных уравнений имеет ненулевые

решения, если определитель системы равен нулю, т. е.

sin l

1 cos l

cos l

sin l

Раскрывая определитель, получаем sin l lcos l 0.

Преобразуем это уравнение к виду

tg l l. (5.58)

Наименьший положительный корень трансцендентного уравнения (5.58) равен приближенно 4,493, т. е.

l 4,493.

(5.59)

Подставим в формулу (5.59) соотношение (5.54), учитывая, что P Pкр, имеем

Pкр l ,

откуда

Pкр l2 2. EI

Из полученного равенства находим искомую критическую силу:

P	2EI	20,187	EI	.

кр	l2		l2

Нижеследующие примеры иллюстрируют применение дифференциальных уравнений при решении задач экономического характера.

Пример 50. Эластичность и функция спроса.

Если известна эластичность спроса на некоторый товар, то мож-

но найти функцию спроса. Пусть эластичность q 1 для любых

значений спроса p. Найти функцию спроса.

Решение. Пользуясь определением эластичности, имеем

q	p	dx	,	(5.60)

	x dp

тогда получаем дифференциальное уравнение с разделяющимися переменными

или

x dp

Интегрируем и получаем уравнение спроса:

3ln

lnC x3

px3

Получено общее решение; для определения C нужна дополни-

тельная информация, например,

p(2) 5. Тогда, очевидно,

C 40

и уравнение спроса принимает вид px3 40.

Пример 51. Найти функцию спроса, если известно значение це-

ны p в некоторой точке x и эластичность имеет вид q x 100, если x

0<x<100; p(10)=90.

Решение. Согласно уравнению (5.49) и условию задачи, имеем

x 100

x dp

или, разделяя переменные в этом дифференциальном уравнении,

x 100

Интегрируем уравнение:

x 100

ln p lnC

x 100

Cp.

x 100

находим C:

С 90 С 1, то-

Используя условие Коши,

гда функция спроса p 100 x.

Пример 52. Функции спроса и предложения.

В простейших случаях предполагается, что спрос и предложение на рынке зависят только от цены товара. В более сложных случаях учитывается их зависимость от изменения цены, т. е. от производной. При этом для определения равновесной цены используется дифференциальное уравнение.

Пусть функции спроса и предложения на некоторый товар имеют вид

x 30 p 4	dp	;	x 20 p	dp	.

	dt			dt

А. Найти зависимость равновесной цены от времени, если p(0)=7.

Б. Найти lim p. Является ли равновесная цена устойчивой?

В. Построить график изменения цены. Решение. А. По условию, имеем

30 p 4

20 p

тогда

5dp

10 2p

10 2p 5

ln10 2p

t C ln10 2p 0,4t 2C

10 2p e 0,4t 2C 2p 10 e 0,4t 2C.

Подставляем в общее решение начальное условие, находим произвольную постоянную:

	14 10 e 2C e 2C 4.
Тогда 2p 10 4e 0,4t		и окончательно		P
получаем				P
получаем			7
	p 5 2e 0,4t.		7
	p 5 2e 0,4t.		5
Б.	lim p 5, поэтому равновесная		5	t
Б.	lim p 5, поэтому равновесная			t
	t

цена является устойчивой.

В. На рис. 6 представлен график

Рис. 6

изменения цены.

Пример 53. Пусть y(t) объем продукции некоторой отрасли, реализованной к моменту времени t. Будем считать, что вся производимая отраслью продукция реализуется по некоторой фиксированной цене p, т.е. выполнено условие ненасыщенности рынка. Тогда доход к моменту времени t составит Y(t) py(t). Пусть I(t) величина инвестиций, направляемых на расширение производства. В модели естественного роста полагают, что скорость выпуска продукции (акселерация) пропорциональна величине инвестиций, т. е. (считая, что инвестиционный лаг равен нулю)

		y (t) lI(t).		(5.61)
Полагая, что величина инвестиций I(t) составляет фиксирован-
ную часть дохода, имеем
		I(t) mY(t) mpy(t),		(5.62)
где m – коэффициент пропорциональности (норма инвестиций),
0 m 1.
Тогда из равенств (5.61) и (5.62) следует
		y (t) mply(t).		(5.63)
Таким образом, имеем дифференциальное уравнение первого
порядка с разделяющимися переменными.
Пусть теперь кривая спроса имеет вид p(y) 3 2y,				норма
акселерации	1	1,5; норма инвестиций	m 0,6; y(0) 1. Найти объ-

	l

ем реализованной продукции и его значение при t=2.

Решение. Для заданных условий уравнение (5.63) принимает вид y 0,4(3 2y)y.

Тогда, разделяя переменные, имеем

																				dy				0,4dt.								(5.64)
																		(3 2y)y						0,4dt.								(5.64)
																		(3 2y)y
		Интегрируем левую часть уравнения:																												3
		dy							1					dy			1							dy		1		d(y		3	)
		dy							1					dy			1							dy		1		d(y			)
																													4
	(3 2y)y										2	y	2		3	y			2					3 2	9	2		3	2			9
															2						y						y
																					y						y					16
																								4	16			4				16
		1	ln		y				3
									3
									2	, следовательно, общий интеграл уравнения (5.64) имеет
								y		, следовательно, общий интеграл уравнения (5.64) имеет
3								y
							3
				y


вид ln						2			1,2 t lnC, откуда, потенцируя, получаем
вид ln									1,2 t lnC, откуда, потенцируя, получаем
					y
																			y			3
																						3
																						2	C e 1,2t.
																						2

																				y

Частный интеграл (с учетом начального условия C 1 ) при-

		3							2
	y	3		1
	y
нимает вид	2				e 1,2t. Выразим из последнего равенства y:
нимает вид	y				e 1,2t. Выразим из последнего равенства y:
	y		2
			3
					y					.
					y					.
			1				e	1,2t
						2(1			)
						2(1			)
			2

Получили частное решение дифференциального уравнения. При

t=2 объем реализованной продукции составит y 3 .

2 e 2,4

Вопросы к разделу «Дифференциальные уравнения

вприложениях»

1.Укажите механический смысл нормальной системы дифференциальных уравнений.

2.Приведите примеры системы дифференциальных уравнений

второго порядка, задающих движение в пространстве и на плоскости материальной точки под действием силы.

3.Математической моделью каких процессов являются линейные дифференциальные уравнения второго порядка, однородные и неоднородные?

4.Приведите примеры задач из области физики, для решения которых требуется составить дифференциальное уравнение (математическую модель) и решить его.

5.Что называется краевой задачей? Приведите примеры постановки краевых задач для дифференциальных уравнений второго и более высокого порядка.

6.Объясните, что называют задачей о собственных значениях и собственных функциях краевой задачи?

7.Приведите примеры экономических задач, для решения которых применяются дифференциальные уравнения.

6. ИНДИВИДУЛЬНЫЕ ЗАДАНИЯ

Вариант 1

1. 1 xy 2y 1 0; y(0) 0. 2. xy y y2.

3. (1 y2)dx xydy.

4.xy2dy (x3 y3)dx.

5.y 2xy 2xe x2 .

6.y		6	; y(1)			(1) 1.
	x3
				2; y (1)	1; y

7.(1 x2 )y xy .

8.y 4y 13y 0.

9.y 4y sin x.

10.y(4) y 0.

11.dydt x 4y;

2x 3y.

Вариант 2

1.y y2 1;y |x 0 3.

2.xdx ydy 0;y(0) 1.

1 y

1 x

3.y 1 x2 1 y2.

4.y y cos2 y.

5.xy y y2x.2

6.x2 y 1 x3;y(1) 1;y (1) 2.

7.3yy (y )2 0.

8.y 5y 6y 0.

9.y 2y 5y x 1.

10.y(4) 2y y 0.

11.dydt 5x 8y;

3x 3y.

Вариант 3

1.y x3 2y.

2.(x2 1)y 2yx2 0;y(0) 1.

3.x(1 y2 )dx (1 x2 )dy.

4.y2dx x2dy xydx.

5.y yctgx sin2 x.

6.y cos2x; y(0) 1; y (0) 1.

7.y 2y(y )3 0.

8.y 9y 0.

9.y 4y 3x.

10.y(4) 4y 0.

11.dtdy 2x 8y;

x 4y.

Вариант4

1. y	2
		4x 1 y .
2.			dy dx.
	x(y 1)

3.yx2 1y x.

4.x2 y (2x y)y 0.

5.xy 2y x4.

6.x

1;y(1)

0, y (1) 1.

7.(1 x

1 0.

(y )

8.y 25y 0.

9.y 16y 3x 1.

10.y(4)

9y 0.

x 5y;

11. dt

7x 3y.

Вариант 5

1.y 3x 1 y 1.

2.xy y 1.

3.(x2 1)dy xydx;y |x 0 2.

4.xy y x2 y2 .

5.x2 y 2xy 3.

6.y 24x 4; y(1) 1; y (1) 1;y (1) 1.

7.2xy y .

8.y 16y 0.

9.y 6y x2 1;y(0) 1; y (0) 2 . 8 27

10.4y y 0.

11.dydt 3x y;

8x y.

Вариант 6

1.x2 4y 1 y .

2.x(y2 1)y y.

3.x(y 2)dy dx.

4.y x y.

5.y x y.

6.y e 2 ;y(0) 0;y (0) 0;y (0) 0,5.

7.y xln x y .

8.y 2y 2y 0.

9.y	3y	3x	2	;y(0)			2
						.
					2; y (0)
						25

10.y 9y 0.

11.dtdy 2x 3y;

x 4y.

Вариант 7

1.x(y 1)dx (x2 1)ydy 0.

2.xy y2 1 0;y(1) 0.

3.y1 x2dy y2dx 0.

4.xyy x2 y.2

5.xy y ex.

6.y 5x4 2x3 x2; y(1) 0,25;y (1) 0.

7.y tgy 2(y )2.

8.3y 2y 0.

9.y 2y 3x;y( 1) 0;y ( 1) e 2.

10.y(4) 16y 0.

11.dtdy 4x y;

8x y.

Вариант 8

1.2xy y.

2.y sin x yln y.

3.(1 y2 )dx xydy 0.

4.y y x;y |x 1 1.

5.y ycosx sin xcosx;y |x 0 0.

6.y cosx; y(0) 0; y (0) 1; y (0) 0.

7.x2 y (y )2.

8.y 5y 0.

9.y 3y x 2; y(0) 0; y (0) 1.

10.y(4) 5y 0.

11.dydt 4x 6y;

4x 2y.

Вариант 9

1.y		y2	1	; y(0) 1.

	x2		1

2.xy y2 3. 2y

3.dy=ytgxdx; y( ) 2.

4.x2 y2 2xyy 0.

5.x2 dy 2xy 3;y( 1) 1. dx

6.y e 3 ;y(0) 3; y (0) 9;y (0) 27.

7.(1 x)y y 0.

8.y 7y 0.

9.y 4y cos x; y(0) 1; y (0) 0.

10.y 2y y 0.

11.dydt x 3y;

3x y.

Вариант 10

1.y 1 y2.

2.2xsin ydx (x2 1)cos ydy 0;y(1) .

3.xyy 1 x2.

4.xy 2xy y.

5.y x2 y x2;y |x 2 1.

6.y 8sin2x 1; y(0) 0; y (0) 2; y (0) 0.

7.y 5y.

8.y 4y 4y 0.

9.y 6y 9y e3x;y(0) 1;y (0) 0.

10.y(4) 16y 0.

11.dydt 5x 4y;

2x 3y.

Вариант 11

1.y 1 x2 y.

2. (1 ex)yy ex;

y(1) 1.

3.x4 y2 dx y1 x2 dy 0.

4.xy y xex .

5.y 3y e x.

6.y 16cos2x; y(0) 0; y (0) 1; y (0) 0.

7.(2y y )y (y )2.

8.y 3y 2y 0.

9.y 9y 6e3x;y(0) 0;y (0) 0.

10.4y(4) 3y y 0.

11.dydt x 2y;

4x 3y.

Вариант 12

1.y y2 y.

2.y sin x ey.

3.(xy2 x)dx (y x2 y)dy 0.

4.(x y)dx xdy 0.

5.xy y x2.

6.y 81e 3x; y(0) 0;y (0) 0;y (0) 0.

7.xy y ln(y / x).

8.y 4y 3y 0.

9.y y 4ex;y(0) 4; y (0) 3.

10.y(4) 16y 0.

11.dydt x 5y;

7x 3y.

Вариант 13

1.y cosx (y 1)sin x.

2.(x2 1)y 2x(4 y);y(0) 1.

3.yx 1dy (y2 1)dx 0.

4.(2x y)dx (x y)dy 0.

5.xy y 3 0.

6.y	1
	(x 1)2
		;y(2) 0;y (2) 1.

7.y (x2 1) 2xy ;y |x 0 1;y |x 0 3.

8.y 4y 0.

9.2y 5y 5x2 2x 1; y(0) 1;y (0) 17.

10.y(4) 5y 0.

11.dydt 5x 8y;

3x 3y.

Вариант 14

1.(1 x)y 1;y(1) 2. y

2.ex 1y ex.

3.xydx 1 x2 dy 0.

4.xy y xex .

5.xy 3y x2.

6.y 1 1; y(1) 0;y (1) 2. x

7.y 2xy 0.

8.y 2y y 0.

9.y 4y e 2x;y(0) 0;y (0) 0.

10.y 6y 9y 0.

11.dt x 5y;dy x 3y.

Вариант 15

1.x3 y y 1.

2.(1 x)y 2;y(1) 4. 2y

3.xln xdy (5 y)dx 0.

4.xy y xtg y.

	y	x
5.xy		x.

6.y x 3e2 5x.

7.(1 sin x)y y cos x 0.

8.y 7y 0.

9.y y 2cos; y(0) 1; y (0) 0.

10.y 10y 25y 0.

11.dydt x 3y;

x 5y.

Вариант 16

1.(y 2)y sin2x; y(0) 1.

2.xy2dx dy.

3.y2 y 2x 1 0.

4.xdy ydx x2 y2 dx.

5.xy y x 1 0.

6.y	24
	(x 2)5
		;y(0) 1; y	(0) 2; y (0) 1.

7.y 1 y x2. x

8.y 4y 0;y(0) 0; y (0) 0.

9.y 4y 6x2 1;y(0) 2; y (0) 3.

10.y(4) 3y 0.

11.dydt 3x y;

8x y.

Вариант 17

1.y 1 sin2x; y(0) 1.

2.1 x2 y x1 y 0.

3.yy xey 0.

4.(x2 y2)y 2xy.

5.xy 2y (x 3)xy2; y(1) 4.

6.(1 x2)y xy .

7.y sin 2x.

8.9y 12y 4y 0; y(0) 0; y (0) 1.

9.2y y 3sin x.

10.y(4) 4y 0.

dx 2x 4y 4t 1;

11. dt			3	x(0) 5; y(0) 1.
	dy	y x		t2,
	dt		2

Вариант 18

1.2x2 y 5y 1 0; y(0) 1.

2.(4x 1)y cos2 2y.

3. dy x2 ydx 0. x 2

4.yy 2y x.

5.y x y xy2.

6.y y ln y ; y(0) 0; y (0) 1.

7.2xy y ; y(9) 8; y (9) 3.

8.y xsin x; y(0) 0; y (0) 0.

9.y 6x 13y x.

10.y(4) y 0.

11.dydt x 4y;

2x 3y.

Вариант 19

1.y ctgx y 2; y(0).

2.3y y 3x 0.

3.(xy2 x)dx (x2 y y)dy 0.

4. xy y(1 ln y); y(1) 1 .

x e

5.t2 ds 2ts 3; s( 1) 1. dt

6.y xln x y ; y(e) e 1; y (e) 1.

7.y 21 y ; y(0) 5; y (0) 1.

8.y sin2 x; y(0) 5; y (0) 1; y (0) 0.

9.y y x 1.

10.y(4) 8y 0.

11.dtdy 2x 8y;

x 4y.

Вариант 20

1.1 ln ydy xydx 0.

2.y 2y 1 0.

3.x2 1dy yxdx 0.

4.y x2 y2 xy 0.

5.y y sin x; y( ) 1.

xx 2

6.y (x2 1) 2xy ; y(0) 1; y (0) 3.

7.	yy					2	1.
7.	yy		(y )				1.
8.	y			4	x sin2x; y(
		sin							) 0;			) 2;			) 1.
		sin						2	) 0;	y (	2	) 2;	y (	2	) 1.
								2			2			2

9.y y 2cos x.

10.y(4) 16y 0.

11.dydt 5x 4y;

2x 3y.

Вариант 21

1.y ytg2x 0.

2.xy _3y 2 0.

3.1 yy x 1 0.

4. y ex y. x

5. (1 x2)y xy xy2; y(0) 0,5.

6. y cosx y sin x 0; y(0) 1; y (0) 2. 4

7.3yy (y )2 0.

8.y (x 5)2 1; y( 1) 1 ; y ( 1) 1.

12 4

9.y 6y 9y 10sin x.

10.y 2y 0.

11.dtdy 7x 2y;

3x 2y.

Вариант 22

1.(1 x2)y xy 0.

2.xy y 3 0.

3.y tgy 2x2.

4.xdy (y 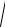x2 y2 )dx.

5.3y2 y y3 x 1; y(1) 1.

6.xy (1 2x2)y ; y(1) e 1; y (1) e.

7.y (y )2 0; y(2) ln(2e); y (2) 0,5.

8.y ln x.

9.y 2y 8y 3sin x.

10.y(4) 5y 0.

11.dtdy 2x 4y;

x 3y.

Вариант 23

1.x2 y x2 1 0.

2.xy 3 y 0.

3.y cos x (y 1)sin x.

4.xy 2xy y.

5.tds 2sdt t3 lntdt.

6.y 2y(y )2 0.

7.y x y ln y ; y(1) 0; y (1) e.

8.y 2y y x2 1.

9.y(4) cos2 x; y(0) 1 ; y (0) 0; y (0) 1.

32 8

10.y y 0.

11.dydt 6x 3y;

8x 5y.

Вариант 24

1. xyy 1 x2; y(1) 1.

2. y cos2	x	y	.

		ln y

3.ydx (4 x2)ln ydy 0.

4.xy y2 (2x2 xy)y .

5.xy y ln x 1.

6.xy ln x y .

7.yy (y )2.

8.y 4cos2x; y(0) 0; y (0) 0.

9.y 2y 8y 16x 4; y(0) 2; y (0) 6.

10.y(4) 3y 4y 0.

11.dydt 3x 2y;

2x 8y.

Вариант 25

1.	2x	1 y	2					2	).
					y		(1 x
2.	y sin x				y	.

				ln y

3.x1 y2dx y(4 x2)dy 0.

4.y y sin2 y.

5.y cos x ysin x 1; y(0) 2.

6.y xln x y ; y(e) e 1; y (e) 1.

7.y 2y 5y 0; y(0) 1; y (0) 2.

8.y sin 2x x.

9.5y 4y 2x 1.

10.4y(4) 3y y 0.

11.dt x 5y;dy x 3y.

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021283.85 Кб286.pdf
#
07.01.2021719.22 Кб10860.pdf
#
07.01.2021720.12 Кб1861.pdf
#
07.01.2021720.35 Кб4862.pdf
#
07.01.2021720.42 Кб44863.pdf
#
07.01.2021720.66 Кб19864.pdf
#
07.01.2021720.79 Кб6865.pdf
#
07.01.2021721.47 Кб1866.pdf
#
07.01.2021721.94 Кб1867.pdf
#
07.01.2021721.94 Кб0868.pdf
#
07.01.2021722.11 Кб8869.pdf