Вопросы к разделу «Дифференциальные уравнения первого порядка»

1.Укажите виды записи дифференциального уравнения первого порядка и назовите их.

2.Что называют задачей Коши? Дайте геометрическую интерпретацию задачи Коши.

3.Сформулируйте теорему Коши о существовании и единственности решения задачи Коши.

4.Что называют особым решением дифференциального уравнения? В какой ситуации появляется особое решение?

5.Какие дифференциальные уравнения являются уравнениями с разделяющимися переменными? Укажите метод их решения.

6.Как определить, что дифференциальное уравнение является однородным? Укажите метод решения.

7.Какие дифференциальные уравнения называют линейными, уравнениями Бернулли? Какие методы решения линейных дифференциальных уравнений вы знаете?

8.Как определить, что дифференциальное уравнение является уравнением в полных дифференциалах?

3.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

3.1.Дифференциальные уравнения второго порядка. Общие вопросы

В общем случае дифференциальное уравнение второго порядка

имеет вид

(3.1)

т. е. связывает независимую переменную x,искомую функцию y и ее

18

называется общим решением уравнения (3.1) или (3.2), если C1,C2 она удовлетворяет уравнению (3.1) [или уравнению (3.2)]. Если решение получено в неявном виде

то его называют общим интегралом уравнения (3.1) или (3.2).

С геометрической точки зрения общее решение (3.3) и общий интеграл (3.4) определяют на плоскости двухпараметрическое семейство кривых (интегральных кривых). На уравнения (3.1),(3.2) часто накладываются начальные условия в виде

В этом случае говорят, что нужно решить задачу Коши, т. е. из семейства интегральных кривых (3.3) или (3.4) выделить ту, которая проходит через заданную точку (x0, y0)и имеет в этой точке касательную, образующую с положительным направлением оси OX угол0, такой, что tg 0 y (x0).

Теорема Коши. Если правая часть f (x, y, y ) (2.3) и ее частные производные по y и y непрерывны в окрестности начальных значений (x0, y0, y0), то существует единственное решение y y(x) уравнения (3.2), удовлетворяющее начальным условиям (3.5).

Если условия теоремы Коши нарушаются, то могут возникать особые решения.

Особым решением называют такое решение дифференциального уравнения, которое во всех своих точках не удовлетворяет свойству единственности, т. е. в любой окрестности точки (x, y) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

19

общее решение дифференциального уравнения:

Решить дифференциальные уравнения. Найти частное решение (частный интеграл), если даны начальные условия.

3.1.xy(4) 1.

3.2.y x 1.

вид F(x,z,z ) 0. Порядок уравнения понижен, далее решаем уравнение первого порядка относительно неизвестной функции z(x), после чего находим решение уравнения (3.6).

Пример 15. Решить дифференциальное уравнение x2 y xy 1. Решение. Уравнение не содержит явно функцию y. Сделав

замену y z(x); y z (x), получим

20

первого порядка, которое можно решить с помощью замены z uv. Подставив это выражение в (3.7), получим

Приравниваем выражение в скобках к нулю: xv v 0,

находим функцию v:

Подставляя функцию v в (3.8), находим u:

xu 1 du dx u ln x lnC1 u lnC1x . x

Обобщим рассмотренный случай для уравнения n-го порядка

вида

F(x,z,z ) 0.

Решаем далее дифференциальное уравнение первого порядка, найдем функцию z(x), после чего, интегрируя (n 1) раз, найдем функцию y.

Пример 16. Решить дифференциальное уравнение y (y )2. Решение. Сделаем замену y z, тогда получим уравнение пер-

вого порядка относительно функции z(x):

dz z2. dx

Разделим переменные и проинтегрируем:

21

Возвращаемся к первоначальной переменной:

y 1 . x C1

Последовательно интегрируя, получаем y ln(x C1) C2;

y (x C1)ln(x C1) x C1 C2x C3; y (x C1)ln(x C1) x(1 C2) C1 C3.

Здесь можно заменить (1+С2) на С2, а (С1+С3) на С3, тогда общее решение примет вид

y (x C1) ln(x C1) C2x C3.

Решить дифференциальные уравнения. Найти частное решение (частный интеграл), если даны начальные условия.

3.5.x2 y (y )2.

3.6.2xy y (y )2 1.

3.7.xy y 1 x.

3.8.xy(4) y ex.

3.9.(1 x2)y 2xy 0; y(0) 0; y (0) 3.

не содержит в явном виде переменную x, за новое независимое переменное берем y , а за неизвестную функцию возьмем y p(y), тогда

уравнение (3.10) приводится к уравнению первого порядка относительно функции p(y): F(y, p, p ) 0.

Пример 17. Найти частное решение дифференциального урав-

22

Решение. Уравнение не содержит в явном виде переменную x, поэтому делаем замену (3.11). После замены данное уравнение будет уравнением первого порядка относительно функции p(y):

23

Решить дифференциальные уравнения. Найти частное решение (частный интеграл), если даны начальные условия.

3.11.yy (y )2 0.

3.12.y3y 1; y(1) 1; y (1) 1.

22

3.13.y (y )2 y (y 1) 0; y(0) 2; y (0) 2.

3.3.Линейные дифференциальные уравнения

спостоянными коэффициентами

Уравнение вида

где коэффициенты p1, p2,..., pn 1, pn постоянные (действительные) числа; f (x) непрерывная на (a,b) функция; x независимая переменная; y(x) искомая функция, называется неоднородным линейным дифференциальным уравнением или уравнением с правой частью.

Если f (x) 0, то уравнение (3.15) принимает вид

и называется однородным линейным дифференциальным уравнением.

Общее решение однородного линейного дифференциального уравнения (3.16) имеет вид

где y1(x), y2(x),...,yn(x) n линейно независимых частных решений однородного уравнения (3.16); С1,С2,...,Сn произвольные постоянные.

Система функцийy1(x), y2(x),...,yn(x)называется линейно зави-

Если тождество (3.18) имеет место только тогда, когда

1 2 ... n 0,

24

то система функций y1(x), y2(x),...,yn(x) называется линейно незави-

симой.

Пример 18. Функции

1,x,x2,...,xn

линейно независимы в интервале ( , ), а также в любом конечном интервале. Допустив противное, получили бы равенство

0 1x 2x2 ... nxn 0

для всех рассматриваемых значений x и не всех , равных нулю. Однако написанное равенство есть алгебраическое уравнение степени n, которое имеет ровно n корней, поэтому может быть справедливым не более как для n значений x.

sin2 x cos2 x 1 0.

Определителем Вронского (вронскианом) для системы функций y1(x), y2(x),...,yn(x), имеющих непрерывные производные до порядка (n 1) включительно, называется определитель вида

В частности, вронскиан для системы двух функций y1(x) и y2(x) есть определитель второго порядка:

Справедливо утверждение: для того, чтобы система функций y1(x), y2(x),...,yn(x) была линейно независимой, необходимо и достаточно, чтобы определитель Вронского, составленный для этих функций, был не равен нулю.

25

Общее решение неоднородного линейного уравнения (3.15) имеет вид

(3.15).

Отметим, что линейно независимая система частных решений однородного уравнения называется фундаментальной системой ре-

шений.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами второго порядка

Рассмотрим уравнение

где p,q R.

Согласно (3.17), общее решение уравнения (3.20) имеет вид

где y1(x), y2(x) образуют фундаментальную систему решений уравнения (3.20) [т.е. y1(x), y2(x) линейно независимые частные решения этого уравнения].

где действительное или комплексное число, которое надо определить.

Так как функция (3.22) есть решение уравнения (3.20), подставим ее и ее производные y e x; y 2e x в это уравнение, получим

Уравнение (3.24) называется характеристическим уравнением, а

26

его корни – характеристическими числами дифференциального уравнения (3.20).

При решении уравнения (3.24) возможны три случая. Случай 1: корни уравнения 1, 2 R и 1 2 . Тогда, согласно(3.22), имеем два частных решения:

Составим определитель Вронского для этих функций.

y x 0 1; y x 0 2.

Решение. Общее решение имеет вид (3.21). Найдем y1, y2. Для этого составляем характеристическое уравнение

2 2 5 2 0.

Корни его действительные и разные: 1 2; 2 1, поэтому, 2

1 x

согласно формулам (3.25), y1 e 2x; y2 e 2 частные (линейно независимые) решения, тогда можем записать общее решение данного дифференциального уравнения в виде формулы (3.26):

27

Подставим найденные значения произвольных постоянных в общее решение (3.27) и найдем частное решение

y 5e 2x 8e 12x . 3 3

Случай 2: корни уравнения 1, 2 R и 1 2.

Тогда одно частное решение уравнения, согласно (3.22), есть y1 e 1x .

В качестве второго частного решения можно взять функцию y2 xe 1x ,

вчем легко убедиться непосредственной подстановкой этой функции

вуравнение (3.20). Вычислим определитель Вронского для этих функций:

частные решения дифференциального уравнения (3.20), поэтому общее решение имеет вид

Определитель Вронского для этих функций

28

мы и общее решение дифференциального уравнения с учетом формулы (3.21) имеет вид

Пример 22. Найти частное решение дифференциального уравнения y 4y 29y 0 при условии y x 0 0, y x 0 15.

Решение. Составляем характеристическое уравнение

2 4 29 0.

Корни уравнения комплексно-сопряженные:

Найденные значения произвольных постоянных подставим в общее решение, получаем частное решение данного дифференциального уравнения:

29

y 3e 2x sin5x.

Пример 23. Найти общее решение дифференциального уравне-

ния y 8y 0.

Решение. Общее решение однородного дифференциального уравнения имеет вид (3.21). Найдем y1(x) и y2(x). Для этого составим характеристическое уравнение

2 8 0;

находим корни этого уравнения:

1,2 8 или 1,2 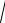( 1)8, или 1,2 8i,

тогда 1,2 22i; в этом случае 0; 22 и, согласно (3.30),

y1(x) cos22x; y2(x) sin22x,

а учитывая формулу (3.31), получаем общее решение данного уравнения:

y C1 cos22x C2 sin22x.

Обобщение на случай линейного однородного дифференциального уравнения n-го порядка

Рассмотрим теперь линейное однородное дифференциальное уравнение n-го порядка (3.16). Общее решение этого уравнения дает формула (3.17). Чтобы найти частные решения y1, y2,...,yn , составляем характеристическое уравнение

n p1 n 1 p2 n 2 ... pn 1 pn 0.

Решая его, находим n корней. Учитывая характер полученных корней, выписываем частные линейно независимые частные решения:

а) каждому однократному действительному корню соответствует решение

e x ;

б) каждому r- кратному действительному корню соответствует r линейно независимых частных решений

e x,xe x,x2e x,x3e x,...,xr 1e x;

в) каждой паре однократных комплексно-сопряженных корней1 i; 2 i соответствуют два линейно независимых частных решения

г) каждой r-кратной паре комплексно-сопряженных корней

30

i соответствуют 2r линейно независимых частных решений

….……………………………… xr 1e x cos x, xr 1e x sin x.

Всего получаем n линейно независимых частных решений. Далее записываем общее решение по формуле (3.17).

Пример 24. Найти общее решение дифференциального уравне-

ния y(4) 2y y 0.

Решение. Это уравнение четвертого порядка, поэтому общее решение уравнения имеет вид [см. (3.17)]

y C1y1 C2 y2 C3y3 C4 y4 ,

где y1, y2, y3, y4 частные линейно независимые решения. Составляем характеристическое уравнение

4 2 2 1 0.

Найдем его корни: ( 2 1)2 0, каждую скобку приравниваем

Общее решение:

y C1 cos x C2 sin x C3xcosx C4 sin x.

Пример 25. Найти общее решение дифференциального уравне-

ния y 8y 0.

Решение. Уравнение третьего порядка, поэтому общее решение уравнения имеет вид [см. (3.17)]

y C1y1 C2 y2 C3y3 ,

где y1, y2, y3 частные линейно независимые решения данного дифференциального уравнения.

Составляем характеристическое уравнение

3 8 0.

Решаем это уравнение и находим его корни: ( 2)( 2 2 4) 0;

31

Здесь имеем действительный корень кратности 1, которому, согласно пункту а), соответствует частное решение

y1 e2x .

Паре однократных комплексных сопряженных корней, согласно пункту в), соответствует два частных решения:

Общее решение дифференциального уравнения y C1e2x C2e x cos3x C3e x sin3x.

Пример 26. Найти общее решение уравнения y y 0. Решение. Уравнение третьего порядка, следовательно, общее

решение есть функция

y C1y1 C2 y2 C3y3 ,

где y1, y2, y3 частные линейно независимые решения дифференциального уравнения.

Составляем характеристическое уравнение

3 2 0.

Действительный корень, равный нулю, имеет кратность 2, следовательно, согласно пункту б), ему соответствуют два частных решения:

y1 e0 x; y2 xe0 x .

Действительный корень, равный минус единице, имеет кратность 1, поэтому, согласно пункту а), ему соответствует частное решение

y3 e x.

Теперь можем записать общее решение уравнения y C1 C2x C3e x.

Пример 27. Найти общее решение уравнения y(4) y 0. Решение. Уравнение четвертого порядка, поэтому общее реше-

ние имеет вид

y C1y1 C2 y2 C3y3 C4 y4 ,

где y1, y2, y3, y4 частные линейно независимые решения дифференциального уравнения.

Составляем характеристическое уравнение

32

4 1 0.

Уравнение имеет четыре комплексных корня, которые можно найти по формуле Муавра

Здесь будет использован другой подход для решения двучленных уравнений – разложение на множители.

4 1 ( 4 2 2 1) 2 2 ( 2 1)2 2 2( 2 1 2 )( 2 1 2 ).

Так как 4 1 0, приравниваем каждую скобку нулю:

Каждой однократной паре комплексных сопряженных корней соответствуют два частных решения: