2.1.xydx (x 1)dy 0.

2.2.y2 1dx xydy.

2.3.xyy 1 x2.

2.4.xy y y3.

2.5.y ctgx y 2; y(0) 1.

2.6.xy y y2.

2.7.y y(1 ex) ex; y(0) 1.

2.8.(xy2 x)dx (x2 y y)dy 0; y(0) 1.

2.3. Однородные дифференциальные уравнения

Функция f(x,y) называется однородной функцией n-го измерения

ная функция первого измерения. При n=0 имеем f (tx,ty) f (x, y).

Уравнение вида y f (x, y) называетсяоднородным,если f(x,y)

однородная функция нулевого измерения.

Уравнение вида P(x, y)dx Q(x, y)dy 0называется однород-

ным, если функции P(x, y),Q(x, y) однородные одного и того же измерения.

Для решения однородных уравнений делаем замену перемен-

ной:

где t t(x).

После замены (2.9) получим уравнение с разделяющимися переменными.

Пример 6.Решить дифференциальное уравнение xdy (x y)dx.

Решение. P(x, y) x y P(tx,ty) tx ty t(x y) tP(x, y). Q(x, y) x Q(tx,ty) tx tQ(x, y).Так как функции P(x, y),Q(x, y)

однородные одного и того же (а именно первого) измерения, то данное уравнение является однородным, поэтому делаем замену (2.9). x(tdx xdt) (x tx)dx xtdx x2dt x(1 t)dx xtdx x(1 t)dx

10

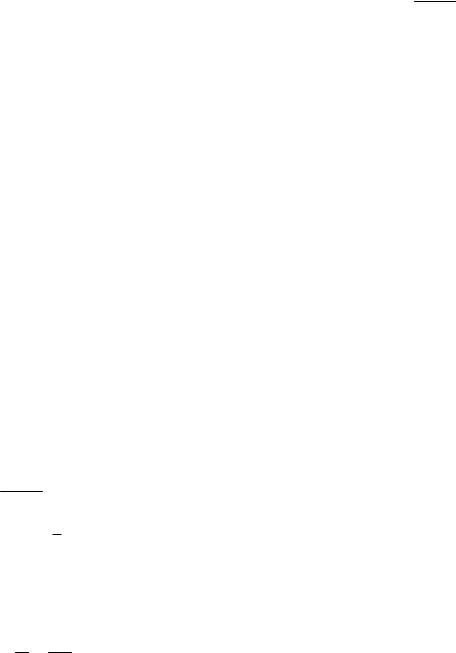
x2dt xdx x2dt.Разделим обе части полученного уравнения на x 0. Тогда имеем dx=xdt – уравнение с разделяющимися пере-

интеграл данного дифференциального уравнения; непосредственной подстановкой в исходное уравнение x=0 убеждаемся, что это тоже решение.

Пример 7. Решить дифференциальное уравнение y x y.

очевидных преобразований получаем уравнение с разделяющимися

Решить дифференциальные уравнения и, если даны начальные условия, найти общий интеграл.

2.9.(x 2y)dx xdy 0.

2.10.y2 x2 y xyy .

2.11.y x y.

x

y

2.12.xy y xe x .

2.13.(x2 y2)dx 2xydy 0; y 0 4.

2.14.(x2 3y2)dx 2xydy 0; y(2) 1.

yy2

2.15.y 4 x x2 ; y(1) 2.

11

2.4. Линейные дифференциальные уравнения

Линейным дифференциальным уравнением первого порядка на-

зывается уравнение вида

Для его решения применяется метод вариации произвольной по-

стоянной. Рассмотрим алгоритм этого метода.

Первый шаг. Решаем сначала однородное уравнение, соответствующее данному линейному уравнению.

Второй шаг. Пусть теперь константа C в (2.11) есть некоторая

Так как функция (2.12) есть решение уравнения (2.10),то, подставив в уравнение это решение, получим тождество, из которого найдем C(x). Предварительно продифференцируем (2.12):

Подставив найденное выражение для C(x) в (2.12), получим общее решение уравнения (2.10).

Пример 8. Решить дифференциальное уравнениеxy 2y 2x4. Решение. Данное уравнение является линейным, так как неизвестная функция и ее производная входят в уравнение в первой сте-

пени. Приведем уравнение к виду (2.10): y 2y 2x3. Далее следуем x

алгоритму, изложенному выше.

Первый шаг.

Тогда имеем общее решение однородного уравнения y Cx2. Второй шаг. Общее решение неоднородного уравнения ищем в

12

виде y C(x)x2; y C (x)x2 2C(x)x. Подставляя в исходное уравнение найденные выражения для y, y , получаем тождество

C (x)x2 2C(x)x 2C(x)x2 2x3 C (x) 2x C(x) x2 C. x

Тогда функция y (x2 C)x2 общее решение неоднородного уравнения. (Отметим, что функция x=0 не является решением уравнения.)

Замечание. Некоторые уравнения становятся линейными, если поменять местами искомую функцию и независимую переменную.

получаем уравнение y dx 2x y3, линейное относительно функции dy

x(y). Решение аналогично решению уравнения (2.10).

Для решения линейного уравнения (2.10) можно также применить подстановку

то из (2.16) найдем v(x), затем из (2.15) найдем функцию u(x), следовательно, из (2.14) найдем неизвестную функцию y.

Такой метод решения часто называют методом Бернулли. Пример 9. Найдем решение дифференциального уравнения из

13

Тогда [см. (2.15)] u x2 2x3 u 2x u x2 C. Следовательно, y (x2 C)x2 общее решение дифференциального уравнения.

Решить дифференциальные уравнения и, если даны начальные условия, найти частные интегралы.

2.16. y ytgx 1 . cos x

2.17.x2 y xy 1 0.

2.18.y x(y xcos x).

2.19.(2x 1)y 4x 2y.

2.20.xy y ex 0; y(a) b.

Сделаем замену z y1 n,после этого уравнение (2.17) становится линейным и решается методом вариации произвольной постоянной.

Пример 10. Решить уравнение Бернулли y 2y y2ex.

z 2z ex. Решаем его методом вариации произвольной постоянной.

Первый шаг.

z Ce2x общее решение однородного уравнения.

Второй шаг. Общее решение неоднородного уравнения ищем в

14

решение уравнения Бернулли. Делили на y2. Проверим, является ли функция y 0 решением исходного уравнения. Да, является.

УравнениеБернуллиможнорешать,применяяподстановку y uv.

Пример 11. Решить дифференциальное уравнение y 2y xy2. x

Решение. Данное уравнение есть уравнение Бернулли [см. формулу (2.17)]. Сделав замену согласно (2.14), получим

u v uv 2uv u2v2x; x

сгруппируем второе слагаемое с третьим:

x

Приравнивая к нулю выражение в квадратных скобках, находим функцию v:

Подставив найденное выражение для функции v в (2.20), находим u:

Решить дифференциальные уравнения и, если даны начальные условия, найти частные интегралы.

2.22.y x y xy2 .

2.23.y y4 cosx ytgx.

2.24.(1 x2)y 2xy xy2; y(0) 1.

2

2.25. y y/ x x2 y4.

15