Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

730.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

657.46 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Формулы имеют вид

i+1

= y

+2k

);

i+1

= z

+ 1

+2m

+m ),

где

k0 = f1(xi ,yi ,zi );

f (x

+ h

h k0

h m0

);

1 i

f (x

+ h

h k1

h m1

);

1 i

k3 = f1(xi

+ h,yi

+ h k2 ,zi

+ h m2 );

m0 = f2(xi ,yi ,zi );

f (x

+ h

h k0

h m0

);

f (x

+ h

h k1

h m1

);

m3 = f2(xi

+h,yi

+h k2 ,zi

+h m2 );

i = 0,1,2...

8. Краевая задача

Примером краевой задачи является двухточечная краевая задача

для ОДУ уравнения второго порядка

′′

′

f (x, y, y )

с граничными условиями, заданными на концах отрезка [a; b]: y(a)=y0,
y(b)=y1.	С
Следует	найти такое решение y(x) на отрезке [a; b], которое

принимает на концах отрезка значения y0, y1.

Если функция f(x, y, y/) линейна по аргументам y, y/, то получаем линейную краевую задачу.

8. 1. Метод стрельбы (пристрелки)

Суть метода заключается в многократном решении задачи Коши для приближенного нахождения решения краевой задачи.

		Пусть надо решить краевую задачу на отрезке [a; b]. Вместо
исходной задачи формулируется задача Коши			/	с уравнением
y	′′	′		(a)=α , где α	–
		= f (x, y, y ) и начальными условиями y(a)=y0, y

некоторое значение угла наклона касательной к искомой интегральной кривой в точке x=a.

Зададим некоторое начальное значение α0 , после чего решим

каким-либо численным методом (методом Эйлера или методом Рунге-Кутта) задачу Коши.

Пусть y = y0 (x,α0 ) решение задачи на интервале [a; b], тогда сравнивая значение функции y0 (b,α0 ) со значением y1 в правом

конце отрезка, можно получить информацию для корректировки угла наклона касательной к решению в левом конце отрезка.

	И
Выбираем новое значение	α1, получаем другое решение со

значением y1(b,α1) на правом конце отрезка и т.д., пока очередное

решение не совпадет со значением y .

То есть решение исходной задачи сводится к нахождению корня

уравнения Ф(α) =0, где Ф(α) = y(b, y0 ,α) − y1. Методы решения этого уравнения аналогичны методам решения нелинейных уравнений.

1 Д

Угол стрельбы выбирается из условия равенства значения
		б		y(b, α) значению	y1 с
интегральной кривой на правой границе
заданной точностью ε.			А
\|y(b, α) – y1\|≤ ε.	и
Интегральная кр вая, полученная из решения задачи Коши с
С

углом, близким к этому значен ю, и будет решением краевой задачи с точностью ε.

9. Решение дифференциальных уравнений в частных производных

В реальных физических процессах искомая функция зависит от нескольких переменных, а это приводит к уравнениям в частных производных от искомой функции. Как и для обыкновенных дифференциальных уравнений (ОДУ), в этом случае для выбора одного конкретного решения, удовлетворяющего уравнению в частных производных, кроме начальных условий, необходимо задавать дополнительные условия (т.е. краевые условия). Чаще всего такие задачи на практике не имеют аналитического решения и приходится использовать численные методы их решения, в том числе

метод сеток, метод конечных разностей и т.д. Мы будем рассматривать класс линейных уравнений в частных производных второго порядка. В общем виде в случае двух переменных эти уравнения записываются в виде

A(x, y)	∂2u	+ B(x, y)		∂2u	+C(x, y)	∂2u	+a(x, y)	∂u	+
	∂x2			∂x∂y		∂y2		∂x
									(9.1)
			∂u +c(x, y)u = F(x, y),
	+b(x, y)
			∂y

где A, B, C, a, b, c – заданные непрерывные функции двух переменных, имеющие непрерывные частные производные, u – искомая функция. Для сокращения записи введем обозначения

.1) вида

	+b(x, y)uy +c(x, y)u = F(x, y)		(9.2)
	+b(x, y)uy +c(x, y)u = F(x, y)
		И
и рассмотрим частный случай (9.2), когда a=b=c=F≡0, т.е.
	Д		(9.3)
	Д		приведено к
	эллипт ческомубАтипу,		приведено к
			канонических
форм)		гиперболическому	типу,

параболическому т пу. Пр чем тип уравнения будет определяться коэффициентами A, B, C, а менно – знаком дискриминанта D = B2 –

координатамиСx, y; если D=0, то (9.3) – параболического типа; если D>0, то (9.3) – гиперболического типа; если D не сохраняет

– 4 A C.	и
Если D<0, то имеем уравнение эллиптического типа в точке с

постоянного знака, то (9.3) – смешанного типа.

Замечание. Если A, B, C – константы, тогда каноническое

уравнение	(9.3)	называется	полностью	эллиптического,
параболического, гиперболического типа.
Введем понятие оператора Лапласа для сокращенной записи
канонических уравнений вида
		∆u = ∂2u	+ ∂2u .	(9.4)
		∂x2	∂y2

Используя это определение, запишем сокращенные канонические уравнения всех трех типов.

1. ∆u = 0 . Это уравнение эллиптического типа, так называемое уравнение Лапласа. В механике это уравнение описывает стационарные тепловые поля, установившееся течение жидкости и т.д.

2. ∆u = − f , где f – заданная непрерывная функция. Это уравнение

Пуассона имеет эллиптический тип и описывает процесс теплопередачи с внутренним источником тепла.

3. a2∆u = ∂∂ut , где a – константа. Не во всех уравнениях в качестве

переменных будут выступать стандартные переменные x, y. Может быть также переменная времени. Это уравнение диффузии описывает процесс теплопроводности и является уравнением параболического

типа.			И
4. ∂2u			И
4. ∂2u	= a2∆u, a – константа. Это уравнение			гиперболического
∂t2			Д
типа – так называемое волновое уравнение – и оно описывает процесс
распространения волн.
9.1. Метод сеток для решения смешанной задачи для уравнения
	параболического типа
		б		найти искомую
Смешанная задача означает, что следует				найти искомую
	и
функцию,	удовлетворяющую Азаданному уравнению в частных
производных, краевым, а также начальным условиям. Различить эти
	С

условия можно в том случае, если одна из независимых переменных – время, а другая – пространственная координата. При этом условия, относящиеся к начальному моменту времени, называются начальными, а условия, относящиеся к фиксированным значениям координат, – краевыми.

Рассмотрим смешанную задачу для однородного уравнения теплопроводности

∂u	= k ∂2u ,k = const > 0 .	(9.5)
∂t	∂x2
Задано начальное условие		(9.6)
	u(x,0) = f (x)	(9.6)
и заданы краевые условия первого рода
	u(0,t) = µ1 (t);	(9.7)
	u(a,t) = µ2 (t).	(9.7)
	32

Требуется найти функцию u(x,t), удовлетворяющую в области D

(0<x<a, 0<t≤T) условиям (9.6) и (9.7).

К задаче (9.5) – (9.7) приводит задача о распространении тепла в однородном стержне длины a, на

концах которого поддерживается заданный температурный режим.

При	проведении замены				t →	t
						k
	∂u =	∂2u
получим			,	т.е. k=1.	Задача

	∂t	∂x2
решается методом сеток: строим в
области		D		равномерную
прямоугольную сетку с шагом h по
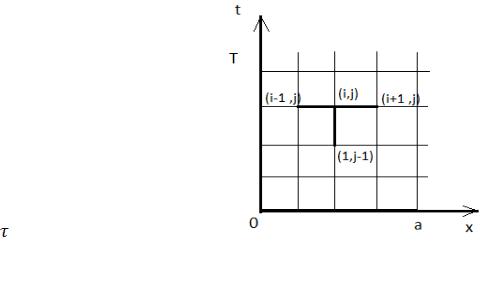
оси x и шагом		по оси t (рис. 9.1).
Приближенные значения искомой							Рис. 9.1. Четырехточечный
					Д
функции	u(xi	,tj) в точках (			xi ,tj)		шаблон неявной схемы

обозначим через uij. Тогда xi=i h; h=a / n; i=0,1,…,n; ti =jτ ; j=0,1,…,

m; τ = T .

Заменим производные в (9.5) разностными отношениями

∂u

ui, j −ui, j−1

+O(τ);

∂t

∂2u

ui+1, j −2ui, j +ui−1, j

+O(h

∂x

В результате получ м неявную двухслойную разностную схему с

погрешностью O(τ + h2 )

ui, j −ui, j−1

ui+1, j −2ui, j +ui−1, j

Используя подстановку λ =

, выразим из этой схемы

(9.8)

ui, j−1

= (2λ +1)ui, j

−λui+1, j −λui−1, j .

Получаем разностную схему, которой аппроксимируем уравнение (9.5) во внутренних узлах сетки. Число уравнений меньше числа неизвестных uij. Из краевых условий получим уравнения

u0,i =µ1(t j );

un, j =µ2(t j ),

которые с (9.8) образуют неявную схему.

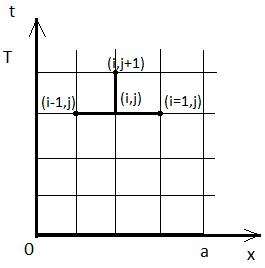
					Получаем				систему		линейных
				уравнений			с			трехдиагональной
				матрицей. Решив ее любым из
				способов (в частности, методом
				прогонки),				получаем			значения
				функции				на		определенных
				временных слоях. Так, на нулевом
				временном				слое			используем
				начальное условие ui,0=f(xi), т.к. j=0.
				На каждом следующем слое искомая
				функция определяется из решения
				полученной системы. Неявная схема
Рис. 9.2. Четырехточечный				полученной системы. Неявная схема
Рис. 9.2. Четырехточечный				устойчива		для				любых	значений
шаблон явной схемы				параметра λ =				τ		> 0.
								τ
								h2


Есть и явная схема (рис. 9.2), но она устойчива только при λ ≤ 1 ,
	h2										2
т.е. при τ ≤	h2	. Вычисления по этой схеме придется вести с малым
	2					И
	2				Д
шагом по τ, что приводит к большим затратам машинного времени.
9.2. Решение задачи Дирихле для уравнения Лапласа методом
			Асеток
Рассмотрим уравнен бе Лапласа
		и		∂2u2	+ ∂2u2 =	0.					(9.9)
		и		∂x	∂y
				∂x	∂y
Будем рассматривать уравнение Лапласа в прямоугольной
области Ω ={(x, y),0 ≤ x ≤ a,0 ≤ y ≤b} с краевыми условиями
		С

u(0, y) = f1 (y); u(a, y) = f2 (y); u(x,0) = f3 (y); u(x,b) = f4 (y),

где f1, f2 , f3 , f4 − заданные функции. Заметим, что чаще всего область

бывает не прямоугольной.

Введем обозначения uij=u(xi,yj). Накладываем на прямоугольную область сетку xi = h i;i = 0,1,...,n;; yj =l j; j = 0,1,...,m. Тогда

xn = h n, ym =l m =b.

Частные производные аппроксимируем по формулам

		∂2u		ui+1, j	−2 ui, j +ui−1, j			2
			=				+O(h			);
		∂x2	=			h2	+O(h			);	(9.10)
		∂x2				h2
		∂2u		ui, j+1	−2 ui, j +ui, j−1
		∂2u	=	ui, j+1	−2 ui, j +ui, j−1		+O(l	2	)
		∂y2	=			l2	+O(l		)
		∂y2				l2
и заменим уравнение Лапласа конечно-разностным уравнением
	ui+1, j −2 ui, j +ui−1, j				+	ui, j+1 −2 ui, j +ui, j−1			= 0,		(9.11)
		h2			+				= 0,		(9.11)
		h2				l2
где i=1,…,n-1, j=1,…,m-1 (т.е. для внутренних узлов).
Погрешность		замены				дифференциального					уравнения

разностным составляет величину O(h2+l2). Уравнения (9.11) и значения ui,j в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений

функции u (x,y) в узлах сетки.				И
Выразим ui,j при h=l и заменим систему
(ui+1, j +ui−1, j +ui, j+1	+ui, j+1 ) / 4;
ui0 = f3 (xi );			Д		(9.12)

uim = f4 (xi );
u0 j = f1 (yi );
unj = f2 (yi ).
б		алгебраических уравнений			можно
Систему (9.12) нелинейных

решить любым итерационным методом (Зейделя, простых итераций и
т.д.).	А
При построен	с стемы использовалась схема типа «крест»

(рис. 9.3). Строим последовательность итераций по методу Зейделя

us+1	=	1	(u(s+1) +u(s)		+u(s) +u(s+1) ),
i, j		4	i−1, j	i+1, j	i, jи+1 i, j−1

где s – текущая итерация. Условие окончания итерационного

процесса

(9.13)

maxi, j

ui(,sj+1)

−ui(,sj)

<ε.

Условие (9.13) ненадежно и на практике используют другой

критерий maxi, j

где ν =

max

i, j

u(s+1)

−u(s)

ui(,sj+1) −ui(,sj)

≤ε(1−ν),

i, j

maxi, j

ui(,sj) −ui(,sj−1)

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021655.91 Кб8726.pdf
#
07.01.2021656.4 Кб7727.pdf
#
07.01.2021656.98 Кб10728.pdf
#
07.01.2021657.3 Кб2729.pdf
#
07.01.2021273.32 Кб173.pdf
#
07.01.2021657.46 Кб36730.pdf
#
07.01.2021657.68 Кб0731.pdf
#
07.01.2021658.17 Кб1732.pdf
#
07.01.2021658.55 Кб6733.pdf
#
07.01.2021659.31 Кб5734.pdf
#
07.01.2021659.47 Кб2735.pdf