
- •1. Математическое моделирование
- •2. Решение систем линейных уравнений
- •2.1. Метод Гаусса
- •2.2. Метод Крамера
- •2.3. Матричный метод
- •2.5. Итерация Гаусса-Зейделя
- •3. Плохо обусловленные системы линейных алгебраических уравнений
- •3.1. Метод регуляризации для решения плохо обусловленных систем
- •3.2. Метод вращения (Гивенса)
- •4. Решение нелинейных уравнений и систем нелинейных уравнений
- •4.1. Решение нелинейных уравнений
- •4.1.1. Отделение корней
- •4.1.2. Уточнение корней: метод итераций
- •4.1.3. Уточнение корней: метод Ньютона
- •4.2. Решение систем нелинейных уравнений
- •4.2.1. Выбор начальных приближений
- •4.2.2. Метод Ньютона
- •4.2.3. Метод итераций
- •5. Метод наименьших квадратов
- •5.1. Линейная регрессия
- •5.2. Показательная регрессионная модель
- •6. Решение обыкновенных дифференциальных уравнений
- •6.1. Метод Эйлера (метод Рунге–Кутта 1-го порядка)
- •6.2. Метод Рунге–Кутта 4-го порядка
- •7. Решение систем обыкновенных дифференциальных уравнений
- •8. Краевая задача
- •8. 1. Метод стрельбы (пристрелки)
- •9. Решение дифференциальных уравнений в частных производных
- •10. Численное интегрирование
- •10.2. Метод трапеций
- •10.3. Метод Симпсона
- •11. Задания для практических занятий
- •11.1. Решение систем линейных уравнений
- •11.2. Решение систем нелинейных уравнений
- •11.4. Решение уравнений методом простой итерации
- •11.6. Решение обыкновенных дифференциальных уравнений
- •11.7. Решение систем обыкновенных дифференциальных уравнений
- •11.8. Решение краевой задачи
- •11.9. Решение дифференциальных уравнений в частных производных
- •11.10. Численное интегрирование
- •Рекомендуемый список литературы
B=lnb;
A=lna.
Получаем линейную регрессионную модель Y=B+A x.
Вычисляем А и В по формулам линейной регрессии, а затем делаем обратное выражение а=exp(A), b=exp(B).
6. Решение обыкновенных дифференциальных уравнений
Уравнение, содержащее производные от искомой функции y(x), называется обыкновенным дифференциальным уравнением (ОДУ).
Общий вид дифференциального уравнения:
|
|
|
|
|
|
|
′ |
′′ |
|
(n) |
) = |
0, |
|
(6.1) |
|
|
|
|
|
|
|
F(x, y, y , y |
,...y |
|
|
||||||
где |
n – наивысший порядок производной, определяет |
порядок |
|||||||||||||
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решением ОДУ называется функция y(x), которая после ее |
|||||||||||||||
подстановки в уравнение (6.1) обращает его в тождество. |
|
||||||||||||||
Общее решение ОДУ имеет вид |
|
|
|
|
И |
(6.2) |
|||||||||
|
|
|
|
|
|
y = y(x,C1,C2 ,...Cn ) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где C1, C2, …, Cn – постоянные интегрирования. |
|
|
|||||||||||||
Частное |
решение получается |
|
из общего при конкретных |
||||||||||||
|
|
|
|
|
|
|
|
|
Д |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
значениях Ci, i =1,n . Эти значения определяются из n дополнительных |
|||||||||||||||
условий. В |
качестве |
таких условий |
могут быть заданы значения |
||||||||||||
|
|
|
|
|
|
|
А |
|
|
|
|
||||
функции и ее про зводных при некоторых значениях аргумента x. |
|||||||||||||||
В зависимости от того, как заданы эти дополнительные условия, |
|||||||||||||||
выделяют 2 типа задач: |
б |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
• |
Задача Коши. Все условия заданы в одной, |
начальной точке, |
|||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
||
поэтому они называются начальными условиями. |
|
|
|||||||||||||
• |
Краевая задача. Условия заданы |
в более чем одной точке, |
|||||||||||||
обычно в начальнойСи конечной. Условия в этом случае называются |
|||||||||||||||
краевыми или граничными. Такая задача может возникнуть только |
|||||||||||||||
при решении ОДУ с порядком выше первого. |
|
|
|||||||||||||
Методы их решения подразделяются на два класса: |
|
||||||||||||||
1) аналитические методы, в которых решение получается в виде |
|||||||||||||||
аналитических функций; |
|
|
|
|
|
|
|
|
|
|
|||||
2) численные |
(приближенные) |
|
методы, |
где |
искомые |
||||||||||
интегральные кривые получают в виде таблиц их численных значений.
Задача решения ОДУ 1-го порядка (задача Коши)
формулируется следующим образом:
25
Найти функцию y(x), удовлетворяющую уравнению |
|
y’ = f(x,y) |
(6.3) |
для x [a; b] при заданном начальном условии y(a) = y0.
Для получения таблицы значений искомой функции y(x) выбирается шаг h и вычисляются значения аргумента xi=x0+ih (i=0, 1, …, n). Затем последовательно находятся yi, близкие к значениям точного решения в точках xi (табл. 6.1).
|
|
|
Таблица 6.1 |
||
|
x |
|
Y |
|
|
|
x0 |
|
y0 |
|
|
|
x1 |
|
y1 |
|
|
|
… |
|
… |
|
|
|
xn |
|
yn |
И |
|
|
|
|
|
||
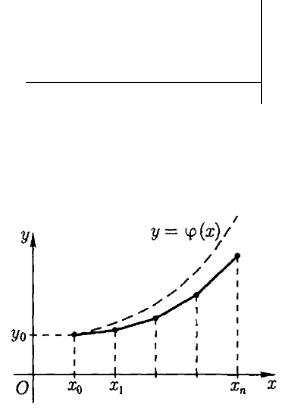
Если на плоскости построить точки с координатами из таблицы и |
|||||
соединить их отрезками, то |
|
Д |
|||
получится так называемая ломаная |
|||||
Эйлера (рис. 6.1). Она будет приближением интегральной кривой y(x).
|
|
А |
|
б |
|
и |
|
|
С |
|
|
Рис. 6.1. Ломаная Эйлера
6.1. Метод Эйлера (метод Рунге–Кутта 1-го порядка)
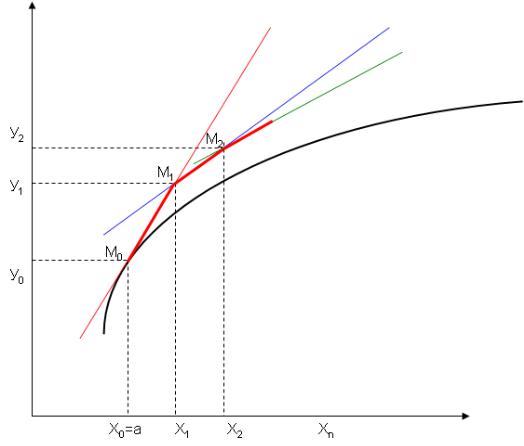
Суть метода заключается в том, что искомую интегральную кривую y=f(x) заменяют ломаной М0, М1, М2 …, звенья которой являются касательными к интегральной кривой.
Разобьем [a; b] на n равных частей – элементарных отрезков, x0, x1,…, xn будем называть узлами сетки, h = (b– a)/n – шаг сетки (рис.
6.2).
26
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
б |
Д |
|
||
|
|
|
|
|
Рис. 6.2. Геометрический смысл метода Эйлера |
|
||||||
|
|
|
|
|
|
|
и |
|
|
|
||
Заменим в уравнении (6.1) Аy’ в точке xi её приближенной оценкой |
||||||||||||
– отношением |
пр ращен й (это |
следует из |
определения |
|||||||||
производной): |
|
|
|
|
|
|
||||||
|
yi′ ≈ ∆yi = |
|
yi+1 − yi |
= |
yi+1 − yi |
. |
|
|
|
|||
|
xi+1 − xi |
|
|
|
|
|||||||
|
|
∆xi |
|
|
h |
|
|
|
||||
Тогда получаем: |
|
|
|
|||||||||
|
yi+1 − yi |
≈ f (Сx , y ). |
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
h |
|
i i |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Отсюда формула Эйлера: |
|
|
|
|||||||||
где i = |
|
|
|
|
|
|
yi+1 ≈ yi + h f (xi , yi ) , |
(6.4) |
||||
0, 1, …., n- |
1 – номер узла. |
|
|
|
||||||||
Зная y0 |
в точке x0 (начальное условие) можно найти y1, затем, |
|||||||||||
используя уже известные значения x1 |
и y1, вычислить x2 и y2 и так |
|||||||||||
далее.
27
6.2. Метод Рунге–Кутта 4-го порядка
На практике наибольшее распространение получил метод Рунге– Кутта 4-го порядка, в котором усреднение проводится по трём точкам, формула Эйлера на каждом отрезке используется 4 раза: в начале отрезка, дважды в его середине и в конце отрезка.
Расчетные формулы метода для дифференциального уравнения (6.3) имеют вид
|
|
|
|
|
|
|
|
|
|
|
|
yi+1 = yi |
+ h (c0 + 2с1 + 2с2 + с3 ) , |
(6.5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
где i = 0, 1, …., n-1 – |
номер узла, у0 = у(х0) – начальное условие, |
|
|||||||||||||||||
c |
0 |
= f (x |
, y |
), c |
= |
f (x |
+ h |
, y |
+ h |
c0 ), |
|
|
|
|
|
||||
|
i |
i |
|
1 |
|
|
i |
2 |
i |
|
|
2 |
|
|
|
|
И |
|
|
c |
|
= f (x |
+ h |
, y |
+h c1 ), c |
= f (x |
+h, y |
+h c |
). |
|
|||||||||
|
2 |
i |
2 |
i |
|
|
2 |
3 |
|
|
i |
|
i |
|
2 |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||
7. Решение систем обыкновенных дифференциальных уравнений |
|||||||||||||||||||
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|||
|
|
Дана система дифференциальных уравнений: |
|
||||||||||||||||
|
|
y′ |
= F |
(x, |
y , y |
,...., y |
), |
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
1 |
|
1 |
2 |
|
n |
|
б |
|
|
|
|
||||
|
|
y2 |
= F2 (x, y1, y2 ,...., yn ), |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
и |
|
|
|
|
|
|
||||
|
|
yn |
= Fn (x, y1, y2 ,...., yn ). |
|
|
|
|
|
|
|
|
|
|||||||
|
|
Рассмотрим задачу Коши для данной системы. Пусть известны |
|||||||||||||||||
|
|
|
|
|
|
С |
x0 |
= a, y1(x0) = y1(0), y2(x0) = y2(0), …, yn(x0) = |
|||||||||||
начальные условия при |
|||||||||||||||||||
= yn(0). Требуется найти |
y1(x), |
|
y2(x),…, |
yn(x), проходящие через |
|||||||||||||||
заданные точки: (x0,y1(0)), (x0,y2(0)), …, (x0,yn(0)). |
|
||||||||||||||||||
|
|
Методы решения одного дифференциального уравнения можно |
|||||||||||||||||
обобщить и на их системы. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
Метод Эйлера: |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y j(i+1) = y j(i) + h Fj (xi , y1(i) , y2(i) ,..., yn(i) ) . |
|
||||||||||||||||
|
|
Метод Рунге–Кутта для системы из двух уравнений с двумя |
|||||||||||||||||
неизвестными: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y′ |
= f1 (x, y, z), |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z′ = f2 (x, y, z). |
|
|
|
|
|
|
|
|
|
|
|
||||||
28
