3. Плохо обусловленные системы линейных алгебраических уравнений

Чем больше значение МА , тем система хуже обусловлена.

Свойства числа обусловленности:

И

1.

МE =1.

Д

2.

МА ≥1.

3.

МА ≥

λmax | / | λmin

, где

λmax ,

λmin –

соответственно

б

максимальное и минимальное собственные числа матрицы А.

4.

МAB ≤ M A * M B .

5. Число обусловленностиАматрицы А не меняется при

умножении матрицы на про звольное число α ≠0.

С

Пусть в системе уравнен й возмущены коэффициенты матрицы

А и правая часть B, т.е.

~

~и

~

δA = A− A,

δB = B− B,δX =

X − X .

В качестве примера рассмотрим систему

1,03x1 +0,991x2 = 2,51;

(3.1)

0,943x2 = 2,41.

0,991x1 +

Решение этой системы

x* ≈1,981,

x* ≈ 0,4735.

1

2

Оценим влияние погрешности правых частей на результат.

Рассмотрим

“возмущенную”

систему

с

правой

частью

B* = (2,505; 2,415) и решим эту систему:

x* ≈ 2,877,

x* ≈ −0,4629.

1

2

Рассмотрим систему

A X = B.

(3.2)

И

Для краткости перепишем эту систему в эквивалентной форме

(A X – B, A X – B) = 0.

(3.2)

Д

Для примера рассмотрим систему

2x − x

=1;

1

1

А

x1 − 2x2

= 2.

Тогда ее можно представить как

(2x

− x

2

−1)2 +(x −2x

2

−2)2 = 0 .

(3.2*)

1

1

Решение системы (3.2) совпадает с решением системы (3.2*).

Если коэффиц енты А

ли B известны неточно, то решение также

С

является неточным, поэтомубвместо равенства (A X – B, A X –

B)=0

можем потребовать пр бл женного выполнения равенства (A X –

B,

A X – B) ≈ 0 и в этомивиде з

адача становится

неопределенной

и

нужно добавить дополнительные условия.

В качестве дополнительного условия вводят требование, чтобы

решение как

можно меньше

отклонялось от

заданного x0 ,

т.е.

(x − x0 , x − x0 )

было минимальным. Следовательно, приходим

к

регуляризованной задаче вида

(Ax −b, Ax −b) +α(x − x0 , x − x0 ) = min,

(3.3)

(AT A +αE)x = AT b +αx0.

(3.5)

Система (3.5) – система линейных алгебраических

уравнений,

(3.5) удовлетворительно обусловлена.

И

На практике пользуются невязкой вида rα = AXα − B , и

эту

невязку сравнивают по норме с известной погрешностью правых

Д

частей δB и с влиянием погрешности коэффициентов матрицы δA.

Если α слишком велико, то rα >>δB или δA. Если α мало,

то

Поэтому проводят серию расчетов, при различных α и в качестве

б0

оптимального значения выбирают то значение α, когда выполнено

следующее условие:

и

rα

≈

δ B

А

+

δA X

.

Для выбора вектора

x нужно знать приближенное решение или

С

же, если приближенное решен е трудно определить, то x0 = 0.

3.2. Метод вращения (Гивенса)

α12

=

a11

, β =

a21

,

a2

+ a2

a2

+ a2

11

21

11

21

где α и β такие, что α2

+ β2

=1,

− β

a

+α a

= 0.

12

12

12

11

12

21

первого и второго уравнений с коэффициентами

α12

и

− β12 . В

результате получим систему

a(1) x

+ a

(1) x

+...

+ a(1) x

=b(1)

,

11

1

12

2

1m

m

1

a22(1) x2

+...+ a2(1m) xm =b2(1) ,

+ a32 x2 +...+ a3m xm =b3 .

(3.6)

a31x1

. . . . . . . .

+ am2 x2

+...+ amm xm =bm .

am1x1

Здесь

a(1)

=

α

a

+ β

a

,

a(1)

=α

a

−

β a

,

b(1)

=α b

+ β

b

,

1 j

12 1 j

12 2 j

2 j

12 2 j

12 1 j

1

12 1

12 2

b(1)

=

α

b

− β

b ,

2

12

2

12

1

И

где j =

.

1, m

Преобразование

системы

(3.1)

к системе (3.6) эквивалентно

Д

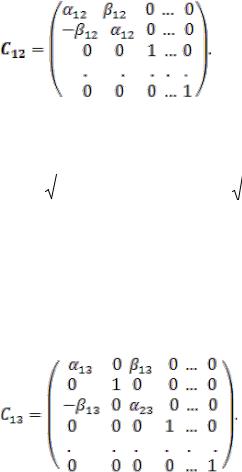
умножению слева матрицы А

и вектора B на матрицу С12 вида

А

Аналогично для исключения

х1

из третьего уравнения вычисляем

числа

a(1)

и

α13

=

β13

=

a

11

31

б

(a

(1)

)

2

+ (a

(1)

)

2

(a

)

+(a

)

(1)

2

(1)

2

11

31

11

31

такие, что α

2

+ β2

=1, α α

31

− β α91)

= 0.

13

13

13

13

11

Затем первое уравнение системы (3.6) заменяем линейной

комбинацией

первого

и

третьего

уравнений

с коэффициентами

α13 , β13 , а третьеСуравнение системы (3.6) заменяем линейной

комбинацией тех же уравнений, но с коэффициентами α13

и − β13.

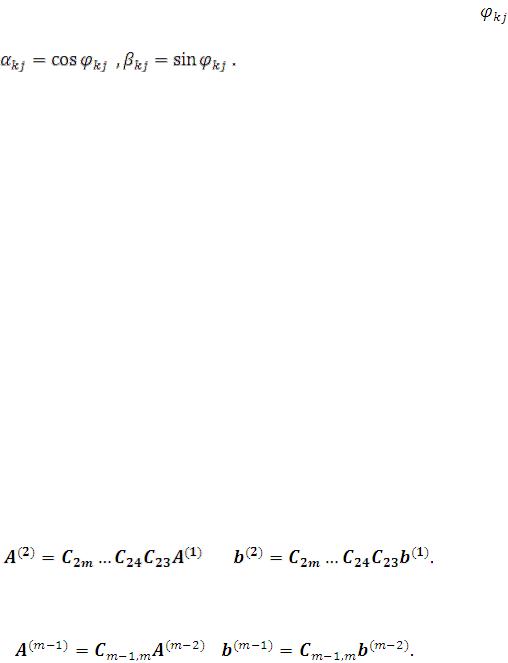
A(1) X = B(1),

(3.7)

где матрица на первом шаге A(1)=С1m…C13C12A, а вектор правых

частей B(1)=С1m…C13C12B.

Здесь и далее через Ckj

обозначена матрица элементарного

преобразования, отличающаяся от единичной матрицы E только

четырьмя элементами.

Действие матрицы Ckj

на вектор X эквивалентно повороту вектора

X вокруг оси, перпендикулярной плоскости OXkXj на угол

такой,

что

Операцию умножения на матрицу Ckj

называют

плоским

вращением или преобразованием Гивенса.

Первый этап состоит из m-1 шагов, в результате чего получается

система

И

a11

x1 + a12

x2

+...

+ a1m

xm = b1

,

(m−1)

(m−1)

(m−1)

m−1

a

(1) x

+...

+ a

Д

2

(1) x

m

= b(1)

,

22

2m

2

(3.8)

......... .............................................

am2 x2

А

= bm .

+... + amm xm

(1)

(1)

(1)

б

В матричной форме получаем A(1) X = B(1).

На втором этапе, состоящем из m-2 шагов, из уравнений системы

и

(3.8) с номерами 3, 4, ... ,

m

исключают неизвестное х2. В результате

получают систему

a(m−1) x

+ a(m−1) x

2

+ a(m−1) x ...+ a(m−1) x

m

=b(m−1)

,

11

1

12

13

3

1m

1

a22(m−1) x2

+ a23(m−1) x3...+ a2(mm−1) xm =b2(m−1) ,

a33 x3 +...+ a3m xm

=b3

,

(2)

(2)

(2)

......... ....................................................... .

С

am3 x3 +...+ amm xm

=bm .

(2)

(3)

(2)

В матричной форме получаем A(2) X = B(2), где

,

После завершения (m-1)-го шага придем к системе с верхней

треугольной матрицей вида

A(m-1) X = B(m-1),

где

,

Обратный ход метода вращений проводится точно так же, как и