722

13

Глава 2. ОПРЕДЕЛИТЕЛИ

§ 1. Основные понятия

Одной из важнейших характеристик квадратной матрицы n-го порядка является определитель (или детерминант), который обозначается A или det A и представляет собой определитель n-го порядка, составленный из тех же элементов, расположенных в том же порядке, что и матрица. Таким образом, если

Таким образом, определитель 2-го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на второй диагонали.

Определение. Определителем 3-го порядка называется число, равное

14

a11 a12 a13

A a21 a22 a23

a31 a32 a33

a11a22a33 a12a23a31 a21a32a13 a13a22a31 a12a21a33 a23a32a11.

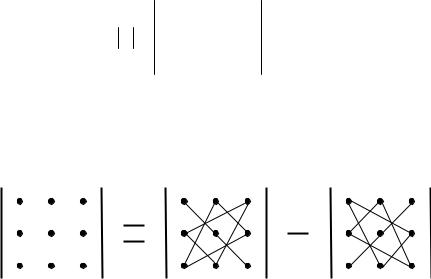
При вычислении определителя 3-го порядка можно пользоваться правилом треугольников (или Саррюса), которое иллюстрируется схемой

Введём понятия минора и алгебраического дополнения для элементов определителя.

Определение. Минором Mij элемента aij определителя n-го порядка называется определитель (n 1)-го порядка, полученный из

Определение. Алгебраическим дополнением Aij элемента aij

определителя называется его минор, взятый со знаком «плюс», если сумма i j − чётное число, и со знаком «минус», если эта сумма нечётна.

Таким образом, по определению Aij ( 1)i j Mij .

15

a11a22a33 a12a23a31 a21a32a13 a13a22a31 a12a21a33 a23a32a11

a11(a22a33 a23a32) a12(a21a33 a23a31) a13(a21a32 a22a31)

a12( 1)1 2 M12 a13( 1)1 3 M13 a11A11 a12A12 a13A13.

Следовательно, определитель 3-го порядка равен сумме произведений элементов первой строки определителя на соответствующие этим элементам алгебраические дополнения.

Теорема. Определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.

Доказательство. Приведём доказательство теоремы для случая определителя 3-го порядка. Разложим определитель по элементам второй строки. Имеем:

a21a32a13 a13a22a31 a12a21a33 a23a32a11.

Написанная сумма совпадает с определителем 3-го порядка. Что и требовалось доказать.

16

Используем разложение определителя по 1-й строке.

4 (2 5) 3 (1 2) 2 ( 5 4) 12 9 18 3.

Разложение определителя по элементам 3-й строки будет выглядеть следующим образом:

2 ( 3 4) 5 ( 4 2) 1 (8 3) 2 10 5 3.

Определители более высоких порядков вычислять по определению достаточно сложно. В этом случае используют теорему о разложении определителя по элементам какой-либо строки и столбца. Например, определитель 4-го порядка запишется в виде суммы произведений элементов строки или столбца на соответствующие им алгебраические дополнения. В данном случае алгебраические дополнения есть определители 3-го порядка.

§2. Свойства определителей

1.Определитель транспонированной матрицы AT равен определителю исходной матрицы A.

3 2 1

Пример. A 2 1 3 .

1 0 1

Разложим определитель по элементам 3-й строки. Имеем:

Транспонируем матрицу A и вычислим её определитель.

17

2. При перестановке двух строк (или столбцов) определитель изменяет знак на противоположный, сохраняя абсолютную величину.

Поменяем местами первую и вторую строчки. Имеем:

4 7

20 ( 21) 41.

35

3.Определитель с двумя одинаковыми строками (или столбцами) равен нулю.

Пример.

4.Если определитель содержит строку (или столбец), состоящую из нулей, то он равен нулю.

Это свойство очевидно, т.к. достаточно разложить определитель по элементам нулевой строки (столбца).

5.Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя.

3 (2 12) 6 (1 8) 3 (3 4) 105.

Вынесем общий множитель элементов первой строки за знак определителя, имеем:

18

3 (2 12) 2 (1 8) (3 4) 3 ( 35) 105.

6.Если элементы какой-либо строки (или столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей, в которых элементами этой строки (столбца) служат отдельные слагаемые:

7.Если все элементы некоторой строки (или столбца) определителя пропорциональны соответствующим элементам другой строки, то определитель равен нулю.

Действительно, по свойству 5 общий множитель элементов строки (или столбца) можно вынести за знак определителя, тогда получим определитель с двумя одинаковыми строками, а он равен нулю по свойству 3.

8.Определитель не изменится, если к элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Пример. Доказать, что

Используя свойства 6, 5 и 3, получим:

Замечание. Это свойство позволяет получить нулевые элементы в какой-либо строке (или столбце), кроме одного элемента, и свести

19

этот определитель n-го порядка к одному определителю (n 1)-го порядка.

Если при вычислении данного определителя применить разложение по элементам любой строки (столбца), то получим четыре определителя 3-го порядка. Этот путь нецелесообразен. Воспользуемся свойством 8 и преобразуем определитель.

Получим нулевые элементы в первом столбце, для этого умножим элементы первой строки последовательно на (−2), (−3), (−4) и прибавим к соответствующим элементам 2-й, 3-й и 4-й строк.

вынесем общие множители 2-й и 3-й строки за знак определителя) =

12 3

9.Сумма произведений элементов какой-либо строки (или столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю.

20

Рассмотрим данное свойство на примере определителя 3-го по-

лителя умножаются на алгебраические дополнения 3-й строки, т.е.

a11(a12a23 a13a22) a12(a11a23 a13a21) a13(a11a22 a12a21)

a11a12a23 a11a13a22 a12a11a23 a12a13a21 a13a11a22 a13a12a21) 0.

Замечание. Очевидно, что определитель единичной матрицы равен единице (detE 1), а определитель диагональной матрицы равен произведению диагональных элементов.

4 0 0

0 0 5

21

4. Сделав линейные преобразования, вычислить определители

4-го порядка:

Ответы: а) 45; б) -44.

Глава 3. НЕВЫРОЖДЕННЫЕ МАТРИЦЫ

§ 1. Основные понятия

Пусть A − квадратная матрица n-го порядка:

Определение. Квадратная матрица A называется невырожденной, если её определитель не равен нулю: det A 0. В противном случае матрица называется вырожденной.

алгебраические дополнения элемента aij матрицы называется союзной

(или присоединённой) к матрице A.

~

Заметим, что в i-й строке союзной матрицы A стоят алгебраические дополнения элементов i-го столбца матрицы A. Поэтому союзная матрица получается следующим образом: в матрице

22