4. Расчет шпинделя

5.4.1. Расчет на жесткость.

Расчет на жесткость предусматривает определение упругих смещений конца шпинделя [5,с.19-21]. Упругие смещения конца шпинделя определяются для двух перпендикулярных плоскостей:

1) смещение у1 лежит в плоскости 1, проходящей через радиальную составляющую силы резания Ру и ось вращения шпинделя;

2) смещение у2 лежит в плоскости 2, проходящей через ось вращения шпинделя и перпендикулярную плоскости 1 (параллельную тангенсальной составляющей силы резания Рz).

Рисунок 5 – Расчетная схема для определения перемещений шпинделя, нагруженного между опорами

Для определения перемещений шпинделей, нагруженных между опорами применяется расчетная схема (рисунок 4). В этом случае перемещение переднего конца шпинделя и его угол наклона определяется по формулам:

, (5.4.1)

где - составляющая силы резания, ; ;

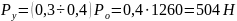– расстояние между передней А и задней В опорами шпинделя;

;

- вылет его переднего конца (консоль); ;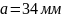

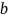– расстояние от передней до точки приложения силы ; ;

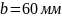– сила, действующая между опорами в рассматриваемой плоскости, Н; силы, действующие на шпиндельный узел от зубчатого колеса:

; ; ;

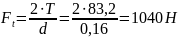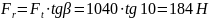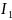- среднее значение осевого момента инерции сечения консоли;

- среднее значение осевого момента инерции сечения шпинделя в пролете между опорами;

– модуль упругости материала шпинделя; для стали 40Х модуль упругости Е = 215000 МПа;

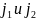- радиальная жесткость передней и задней опор.

Угол поворота шпинделя в передней опоре:

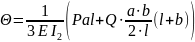, (5.4.2)

Радиальная жесткость условной опоры может быть вычислена по формуле:

, (5.4.3)

где α - фактический угол контакта в подшипнике, изменяющийся под действием предварительного натяга ( α = 26°);

i1 и i2 - число подшипников в опорах 1 и 2;

К – коэффициент, характеризующий распределение нагрузки между телами качения и зависящий от соотношения между силой натяга и радиальной нагрузкой, К=0,7;

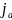- осевая жесткость комплексной опоры, Н/мм:

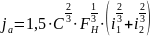, (5.4.4)

где

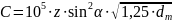
F_Н - сила натяга; F_Н=390 Н;

z- число тел качения в подшипнике; z=12;

d_m - диаметр шарика, мм; d_m=15,08 мм.

.

Осевая жесткость комплексной опоры согласно формуле (5.4.4 ):

.

Радиальная жесткость опор 1 и 2 согласно формуле (5.4.3):

.

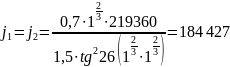
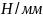Среднее значение осевого момента инерции сечения консоли:

,

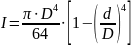где 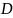- диаметр вала,

- диаметр отверстия.

Осевой момент инерции сечения консоли:

120 576 мм4.

Осевой момент инерции сечения шпинделя в пролете между опорами:

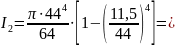183 032 мм4.

По формуле (5.4.1 ) определяем перемещение переднего конца шпинделя в плоскости 1, проходящей через радиальную составляющую силы резания 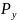и ось вращения шпинделя:

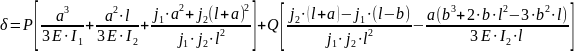
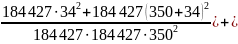
0,007 мм.

Угол поворота шпинделя в передней опоре согласно формуле (5.4.2):

.

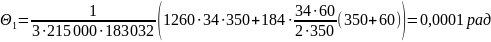По формуле (5.4.1) определяем перемещение переднего конца шпинделя в плоскости 2, проходящей параллельно тангенсальной составляющей силы резания и через ось вращения шпинделя:

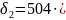
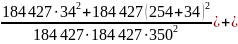
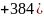0,003 мм.

Угол поворота шпинделя в передней опоре согласно формуле (5.4.2 ):

.

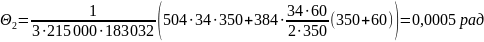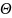Результирующая величина смещения переднего конца шпинделя и угла наклона определяются по формулам:

,

;

,

,

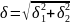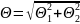что соответствует условию .

Радиальная жесткость шпиндельного узла определяется по формуле:

,

,

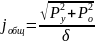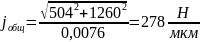Полученное значение жесткости больше минимально допустимого для станков общего назначения.

5.4.2. Расчет динамических характеристик шпинделя

Приблизительный расчет собственной частоты шпинделя, не имеющего больших сосредоточенных масс, проводится по формуле:

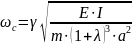, (5.4.5)

где 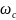- собственная частота шпинделя, с-1;

- масса шпинделя, кг;

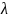- относительное расстояние между опорами, ;

- длина консоли шпинделя, мм;

– осевой момент инерции шпинделя, мм4;

- модуль упругости материала шпинделя, МПа;

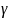- коэффициент, зависящий от , .

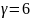Масса шпинделя равна:

,

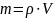где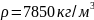 - плотность стали 40Х,

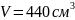- объем шпинделя;

.

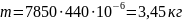Определяем собственную частоту шпинделя по формуле (5.4.5):

.

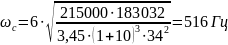Необходимое условие: - выполняется.