3. Выбор схемы коробки скоростей и кинематические расчеты

1. Варианты структурных формул и их анализ

Число ступеней частот вращения шпинделя z при настройке последовательно включенными групповыми пере­дачами (в многоваловых коробках) равно произведению чисел передач в каждой группе (Р_а, Р_b, Р_c ..., P_k), т. е. z = P_aP_bP_c...P_k .

При заданном (или выбранном) числе ступеней частот враще­ния шпинделя z количество групп передач, количество передач в каждой группе и порядок расположения групп может быть различным. Этот выбор в основном и определяет кинематику и конструкцию коробки скоростей.

Для принятого числа ступеней частот вращения шпинделя z = 12 возможен вариант структурной формулы: , ,

, , .

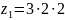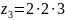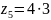Выбираем структурную формулу

Данная структурная формула указывает, что привод включает в себя 3 группы передач, 1 из которых содержит три передачи, а 2 и 3 по 2 передачи.

2. Составление схемы коробки скоростей и построение структурных сеток.

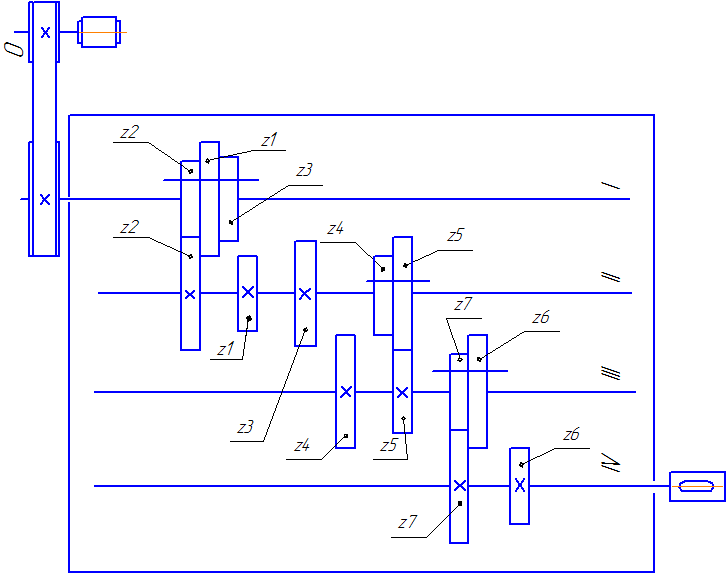
Рисунок 2 - Кинематическая схема коробки скоростей.

Структурные сетки строят для того, чтобы в наглядной форме выявить все возможные варианты и выбрать оптимальный ва­риант структуры кинематических цепей проектируемого станка.

Структурная сетка содержит следующие данные о приводе:

коли­чество групп передач, число передач в каждой группе, относи­тельный порядок конструктивного расположения групп в цепи передач, порядок кинематического включения групп (т. е. их характеристики и связь между передаточными отношениями), диапазон регулирования групповых передач и всего привода, число ступеней частот вращения ведущего и ведомого валов групповой передачи.

Рисунок 3 – Структурная сетка

4.3 Графики частот вращения

График частот вращения отражает частоты вращения всех валов привода, включая валы одиночных передач, необходимых для его компоновки. Построение начинают с цепи редукции, обеспечивающей снижение частоты вращения электродвигателя n_эд. до n_min на шпинделе. Для дальнейшего построения используется структурная сетка.

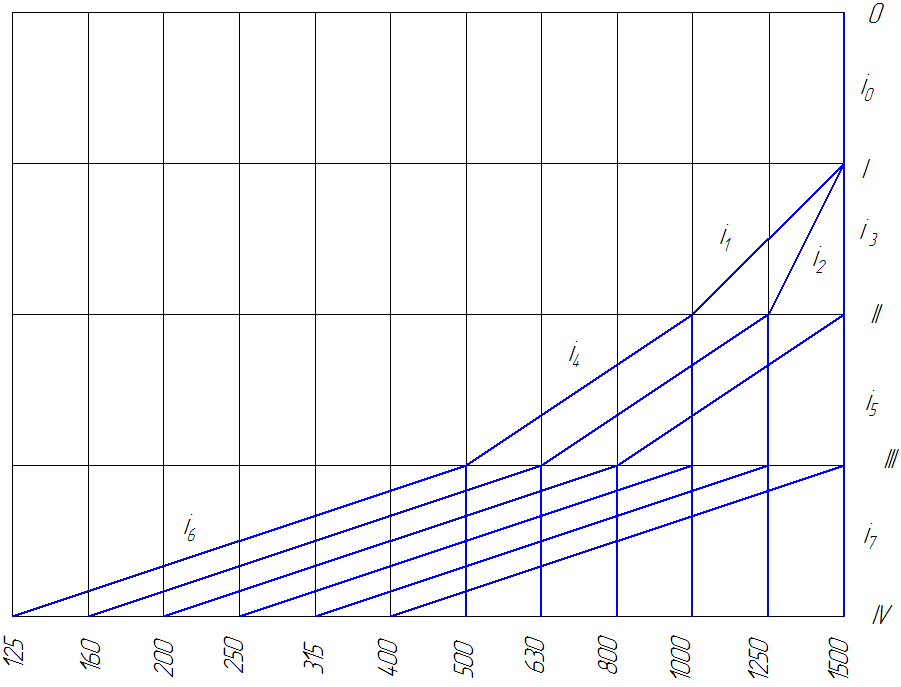
Рисунок 4- График частот вращения.

4.4 Расчет передаточных отношений, чисел зубьев шестерен передач и их модулей

4.4.1 Исходя из постоянства межосевого расстояния, числа зубьев ведущего и ведомого колес определяем по формуле:

,

, (1)

где - числитель передаточного отношения;

- знаменатель передаточного отношения;

- сумма чисел зубьев сопряженных колес;

, (2)

где - наименьшее кратное сумм ,

- целое число,

. (3)

Для определения наименьшего кратного К сумм передаточные отношения выразим в виде простых дробей с числителем и знаменателем , причем так, чтобы были числа, разлагающиеся на простые множители.

Передаточные отношения группы передач между валами I и II:

;

;

.

Следовательно,

= 7+11 = 18 = ;

= 4+5 = 9 = ;

= 1+1 = 2.

Отсюда наименьшее кратное сумм будет К =

Определяем для минимального передаточного отношения по формуле (3):

.

Округляем до целого числа: .

Сумма чисел зубьев сопряженных колес по формуле (2):

Полученную сумму уточняем по нормали Н21-5 [3,с.279].

54.

Определяем числа зубьев сопряженных колес по формулам (1):

,

,

,

,

,

,

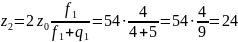необходимое условие выполняется.

Передаточные отношения группы передач между валами II и III:

;

;

Следовательно,

= 1+2 = 3;

= 1+1 =2;

Отсюда наименьшее кратное сумм будет К =

Определяем для минимального передаточного отношения 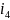по формуле (3):

.

Округляем до целого числа: .

Сумма чисел зубьев сопряженных колес по формуле (2):

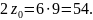
Полученную сумму уточняем по нормали Н21-5 [3,с.279].

54.

Определяем числа зубьев сопряженных колес по формулам (1):

,

,

,

,

- необходимое условие выполняется.

Передаточные отношения группы передач между валами III и IV

;

;

Следовательно,

= 1+4 = 5;

= 1+1 =2;

Отсюда наименьшее кратное сумм будет К =

Определяем для минимального передаточного отношения по формуле (3):

.

Округляем до целого числа: .

Сумма чисел зубьев сопряженных колес по формуле (2):

Полученную сумму уточняем по нормали Н21-5 [3,с.279].

80.

Определяем числа зубьев сопряженных колес по формулам (1):

,

,

,

,

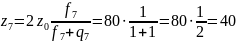- необходимое условие выполняется.

4.4.2 Определяем расчетные крутящие моменты Т, Нм на каждом из валов:

, (4)

где n – частота вращения вала, ;

N – мощность, передаваемая валом, кВт.

Для вала 1:

, где - КПД ременной передачи,

.

Для вала 2:

, где - КПД зубчатой передачи,

- КПД подшипников качения,

.

Для вала 3:

, где - КПД зубчатой передачи,

- КПД подшипников качения,

.

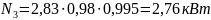
Для вала 4:

, где - КПД зубчатой передачи,

- КПД подшипников качения,

.

4.4.3 Определяем модуль зубчатой передачи, исходя из контактной прочности:

, (5)

где - вспомогательный коэффициент, для прямозубых передач K_d = 770;

z₁ – число зубьев шестерни;

T_n – вращающий момент на шестерне, Нм;

i – передаточное отношение передачи;

δ_НР – допускаемое контактное напряжение, МПа;

, (6)

где – базовый предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов, ,

- коэффициент безопасности, 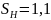[5, с.12],

– коэффициент долговечности,

– коэффициент ширины зуба, принимаем 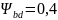[5, с.12]

K_H – коэффициент, учитывающий распределение нагрузки по ширине

венца; по графику определяем: K_H = 1,1 [5, с.13].

Коэффициент долговечности

, (7)

где - базовое число циклов переменных напряжений, циклов,

– эквивалентное число циклов переменных нагружений,

,

где - коэффициент, характеризующий интенсивность типового режима нагружения по контактным напряжениям, [5, с.15],

n – частота вращения колеса, по материалу которого определяются допустимые напряжения,

t – число часов работы передачи за расчетный срок службы, t = 12000ч.

Для шестерни 1 определяем:

по формуле (7): . Принимаем .

,

Для шестерни 4 определяем:

по формуле (7): . Принимаем .

,

Для шестерни 6 определяем:

по формуле (7): 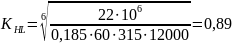. Принимаем .

,

4.4.4 Определяем модуль зубчатой передачи, исходя из изгибной прочности.

, (8)

где – вспомогательный коэффициент, для прямозубых колес =12;

- коэффициент, учитывающий распределение нагрузки по ширине венца при расчете по изгибным напряжениям, [5, с. 13]

- коэффициент формы зуба при расчете на изгиб, зависит от числа зубьев колеса, для z=21 [5, табл. 4.3];

z₁ – число зубьев шестерни;

T₂ – вращающий момент на шестерне, Нм;

– коэффициент ширины зуба, принимаем [5, с.12];

δ_FР – допускаемое напряжение изгиба, МПа;

, (9)

где – базовый предел выносливости зубьев по напряжениям изгиба, МПа,

[6, табл. 5.3]

- коэффициент безопасности, [6, табл. 5.3],

– коэффициент долговечности,

K_FC – коэффициент, учитывающий влияние двухстороннего приложения нагрузки,

K_FC = 1 [5, с.17].

Коэффициент долговечности

, (10)

где – эквивалентное число циклов нагружения,

,

где - коэффициент, характеризующий интенсивность типового режима нагружения по напряжениям изгиба, [5, с.15],

n – частота вращения колеса, по материалу которого определяются допустимые напряжения,

t – число часов работы передачи за расчетный срок службы, t = 12000ч,

a – показатель степеней корня, при твердости материала НВ а = 6.

Для шестерни 1 определяем:

по формуле (10): ,

,

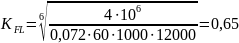Для шестерни 4 определяем:

по формуле (10): ,

,

Для шестерни 6 определяем:

по формуле (10): ,

,

Итак, выбираем большие из модулей зубчатых передач, уточняем согласно нормали Н21-5 [3,с.279]:

для первой группы передач m₁ = 2,5 мм,

для второй группы передач m₂ = 2,5 мм.

для второй группы передач m₃ = 2,5 мм.

4.4.5. Определяем межосевые расстояния по формуле:

Расстояние между валами 1 и 2:

Расстояние между валами 2 и 3:

Расстояние между валами 3 и 4:

4.4.6. Определяем параметры зубчатых колес по формулам:

диаметр делительной окружности , мм,

диаметр впадин , мм,

диаметр выступов , мм,

ширина зубчатого колеса , мм, где =0,1 0,3 – коэффициент ширины зуба,

ширина шестерни

	m,мм	A,мм	,мм
	2,5	67,5	82,5	76	88	20
	2,5	67,5	52,5	46	58		22
	2,5	67,5	75	69	80	20
	2,5	67,5	60	54	65		22
	2,5	67,5	67,5	61	73	20
	2,5	67,5	67,5	61	73		22
	2,5	67,5	90	84	95	20
	2,5	67,5	45	39	50		22
	2,5	67,5	67,5	61	73	20
	2,5	67,5	67,5	61	73		22
	2,5	100	160	154	165	20
	2,5	100	40	34	45		22
	2,5	100	100	94	105	20
	2,5	100	100	94	105		22