
3-й семестр / Лекции / 08 - презентация
.pdf
Если функция ( ) была определена на функция ( ) определена на отрезке [− , ] этом отрезке условиям теоремы Дирихле.
Фурье функцию ( )
( ) → 20 + ∑∞=1( ∙ cos + ∙ sin )
и возвращаясь к исходной функции, следующее представление рядом Фурье:
отрезке [− , ], то и удовлетворяет на Раскладывая в ряд
получим для нее
( ) → |
0 |
+ ∑∞ |
( |
|
∙ cos |
|
+ |
∙ sin |
|
) , |
(4) |
|
|
|
|||||||||
|
2 |
=1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
коэффициенты которого вычисляются по формулам:
0
= |
1 |
|
|
∫− |
( ) , |
||||||
|
|
|
|||||||||
= |
|
1 |
∫− |
( )cos |
|
, = 1,2,3, …, (5) |
|||||
|
|
||||||||||
= |
1 |
|
∫− |
( )sin |
|
, = 1,2,3, … . |
|||||
|
|
||||||||||

Теорема Дирихле остается в силе с той лишь разницей, что в случае произвольного отрезка [− , ] точки = ± заменяются на точки = ± :
( ) = (− ) = 12 ( (− + 0) + ( − 0)).
Равенство Парсеваля принимает вид:
202 + ∑∞=1( 2 + 2) = 1 ∫− 2( ) .
7.5. Ряд Фурье для четных и нечетных функций
|
Если кусочно-непрерывная функция |
|
, определенная на |
|
|
( |
) |
отрезке [− , ], является четной, то |
|
|
|
∫− |
( ) = ∫−0 ( ) + ∫0 ( ) = 2 ∫0 ( ) . |
||
Действительно, сделав замену = −, вычислим
0 0
∫− ( ) = − ∫ (−) = ∫0 ( ) = ∫0 ( ) .
Аналогично устанавливается, что в случае нечетной функции
( ):
0
∫− ( ) = ∫− ( ) + ∫0 ( ) =
= − ∫0 (−) + |
∫0 ( ) = |
= − ∫0 ( ) + ∫0 |
( ) = 0. |

Предположим теперь, что кусочно-дифференцируемая функция( ), определенная на отрезке [− , ], является четной.
Тогда 0 = 1 ∫− ( ) = 2 ∫0 ( ) .
Вычислим остальные коэффициенты Фурье четной функции.
Произведение ( ) |
|
|
также является четной функцией. |
||||||||||||||||||
|
|
||||||||||||||||||||
|
|
1 |
∫ |
|
|
|
|
|
|
2 |
|
∫ |
|
|
|
||||||
= |
( ) |
= |
|
( ) |
, ( = 1,2,3, … ) |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
− |
|
|
|
|
|
|
0 |
|
|
||||||||||
Произведение ( ) |
является нечетной функцией. |
||||||||||||||||||||
|
|
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
( ) |
= 0, ( = 1,2,3, … ). |
||||||||||||||||||
|
∫ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, тригонометрический ряд Фурье четной функции
содержит только косинусы:
( ) → 20 + ∑∞=1 cos , где0 = 2 ∫0 ( ) ,

= |
2 |
∫ |
( ) |
|
, ( = 1,2,3, … ), |
||
|
|
|
|||||
|
0 |
|
|
||||
= 0, ( = 1,2,3, … ).
Равенство Парсеваля приобретает вид:
2 ∫0 2( ) = 202 + ∑∞=1 2.
Если функция ( ) |
|
является нечетной, то произведение |
|||||||||||||||||||||||||||||
( ) |
|
также является нечетной функцией, а произведение |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
- четной. Вычислим коэффициенты Фурье нечетной |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
= |
|
1 |
∫ |
( ) |
|
= 0, ( = 0,1,2,3, … ), |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
= |
1 |
|
|
|
( ) |
|
= |
2 |
|
|
( ) |
|
, ( = 1,2,3, … ). |
||||||||||||||||
|
|
|
∫ |
|
|
|
∫ |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||
|
|
|
Тригонометрический ряд Фурье нечетной функции содержит |
||||||||||||||||||||||||||||
только синусы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
( ) → ∑∞ |
|
|
sin |
, |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а равенство Парсеваля приобретает вид: |
|||||||||||||||||||||||||||||||
2 |
|
|
|
2( ) |
|
|
|
∑∞ |
|
|
2 |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7.6. Разложение функций, заданных на полупериоде, в ряд Фурье только по косинусам или только по синусам
Пусть функция ( ) определена и кусочно-дифференцируема на отрезке [0, ]. Желая получить разложение этой функции в ряд Фурье, доопределим ее на промежутке [− , 0) произвольным образом, сохраняя лишь требование кусочной дифференцируемости. Это дает возможность получать различные разложения одной и той же функции в тригонометрические ряды Фурье на отрезке [0, ].
Если, определяя функцию на промежутке [− , 0), будем полагать, что (− ) = ( ) для всех [− , 0), то получим четную функцию, тригонометрический ряд Фурье которой будет содержать только косинусы.
Если, определяя функцию на промежутке [− , 0), будем полагать, что (− ) = − ( ) для всех [− , 0), то получим нечетную функцию, тригонометрический ряд Фурье которой будет содержать только синусы.
Пример 2. Разложить функцию ( ) = 3 − , заданную на отрезке [0,3], в тригонометрический ряд Фурье по косинусам и в тригонометрический ряд Фурье по синусам. Обосновать сходимость каждого ряда Фурье. Нарисовать графики суммы для каждого ряда Фурье.
Решение.
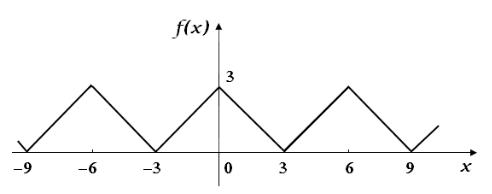
1). Разложение по косинусам.
Доопределим функцию ( ) на промежутке [−3,0) четным образом и продолжим ее на всю числовую ось как периодическую с периодом, равным 6:
( ) = (− ) = 3 − (− ) = 3 + , [−3,0).
Вычислим коэффициенты Фурье этой четной функции:
= 0, ( = 1,2,3, … ).
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
3 |
|
||||||||
0 |
= |
|
|
|
|
∫ (3 − ) = |
|
|
|
(3 − |
|
|
|
)| = 3, |
|
0 |
= |
|
. |
||||||||||||||||||||||||
3 |
|
3 |
2 |
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
∫3(3 − )cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= 3 − |
|
= cos |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
= [ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
] = |
|
|
|
|
|
|||||||||||||
|
= − |
|
|
= |
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
((3 − ) ∙ |
3 |
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||||||||
= |
|
|
|
sin |
|
|
|
|
|
| |
+ |
|
|
|
∫0 |
sin |
|
|
) = |
||||||||||||||||||||||||
3 |
|
|
|
|
3 |
|
|
|
3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
6 |
|
|
(cos − 1) = |
|
|
|||||||||||||||||
= |
|
|
(− |
|
) cos |
|
|
|0 |
|
= − |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
3 |
|
|
2 2 |
|
|
||||||||||||||||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, = 2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
(1 − (−1) |
) = { |
|
|
12 |
|
|
|
|
|
, = 2 + 1. |
|
|
|||||||||||||||||||||||||||||
2 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(2 +1)2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
