Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Математический анализ

Файл:

3-й семестр / Лекции / 06

.pdf

Скачиваний:

Добавлен:

25.12.2020

Размер:

543.3 Кб

Скачать

☆

ЛЕКЦИЯ 6.

Ряд Тейлора

1.Представление функций степенными рядами.

Частичными суммами степенных рядов являются многочлены, что делает степенные ряды удобным средством для приближенных вычислений. Поэтому особое значение имеет вопрос о представлении функций степенными рядами.

Предположим, что заданная функция	f (x)	в некотором интервале с

центром в точке

формуле Тейлора равенство:

для

имеет производные всех порядков. Тогда согласно всех значений x из этого интервала имеет место

f (x)		)	f (x	)	(x x	)	f (x	)	(x x		2	...
f (x)	f (x	)	0		(x x	)	0		(x x	)	2	...
	0		1!		0		2!		0
			1!				2!

f	(n)	(x	)
f		(x	)	(x x		n
		0		(x x	)	n
	n!			0
	n!

R	(x)
n

где	n		- остаточный член формулы Тейлора
	R	(x)

разными способами, например, в форме Лагранжа:

и может быть записан

R	(x)
n

f	(n 1)	(x )	(x

		1

	(n 1)!

x	)	n 1
x	)
0

, где

(x	,
0

При этом n можно выбрать сколь угодно большим, т.е. учитывать в этой

формуле сколь угодно большие степени переменной

(x x0 ) . Естественно

возникает вопрос о возможности представления функции

f (x)

в виде

бесконечной суммы или в виде степенного ряда:

)

f (x

)

f (x

)

(n)

f (x) f (x

)

(x x )

...

(x x

)

...

Такой ряд, независимо от того, сходится он или не сходится к функции

f (x)

в некотором интервале, называется рядом Тейлора этой функции, а его

коэффициенты – коэффициентами Тейлора. Если

x0 0 ,

то данный

степенной ряд называется рядом Маклорена:

f (x)

f (0)

x 2 ...

f (n)

(0)

xn ... .

Условие сходимости ряда Тейлора заданной функции к этой

функции.

Согласно формуле Тейлора разность между значениями функции f (x)

и частичной суммой ряда Тейлора с номером

(n 1)

этой функции равна

остаточному

члену формулы

Тейлора

Rn (x) . Поэтому

справедливо

следующее утверждение.

Теорема. Для того чтобы при некотором значении x значение функции

f (x)	совпадало с суммой ряда Тейлора этой функции, необходимо и

достаточно, чтобы остаточный член формулы Тейлора при этом значении x

стремился к нулю с возрастанием n:			lim Rn (x) 0 .
			n
Рассмотрим функцию:
	1
	x2
	x2	, x 0,
f (x) e		, x 0,
		x 0.
0,		x 0.

Можно показать, что эта функция на всей числовой оси имеет

производные всех порядков, и все ее производные при

x 0

равны 0. Ряд

Маклорена этой функции сходится при всех x, и сумма его тождественно равна 0. Таким образом, данная функция не представляется своим рядом Маклорена ни в какой окрестности точки x 0 .

Для того чтобы выяснить, сходится ли ряд Тейлора заданной функции к этой функции, в ряде случаев оказывается полезным следующее утверждение.

Теорема. Если функция	f (x)	в некотором интервале с центром в точке	x
			0

имеет производные всех порядков и все производные для всех x из этого

интервала ограничены одним и тем же числом:				f	(n)	(x) M	, то	ряд


Тейлора этой функции сходится к самой функции на данном интервале.
Это утверждение применимо к таким элементарным функциям как								e	x	,


sin x ,	cos x	. Например, функции sin x и	cos x	дифференцируемы всюду

бесконечное число раз, и все их производные ограничены по модулю единицей. Значит, эти функции можно разложить в ряды Тейлора на любом интервале с центром в любой точке.

3. Единственность представления функции степенным рядом.

Теорема. Если функция

f (x)

представима на некотором интервале с центром

в точке

степенным рядом: f (x) an (x x0 )n , то этот ряд является рядом

n 0

Тейлора этой функции.

Доказательство. Полагая

x x0

в формуле f (x) an (x x0 )n , получим

n 0

f (x	) a	. Применим к данному степенному ряду теорему о почленном
0	0	. Применим к данному степенному ряду теорему о почленном

дифференцировании:

f (x) an n (x x0 )n 1 ,

n 1

f (x)							a			n (n 1) (x x											)
				n																		n 2	,
				n																0			,
				n 2
. . . . . . . . . .

f	(k )	(x)							a				n (n 1) ...							(n k 1) (x x								)	n k		,
f		(x)							a		n		n (n 1) ...							(n k 1) (x x							0	)
											n																0
					n k
. . . . . . . . . .
Полагая в этих равенствах																	x x					, получим:
Полагая в этих равенствах																					0	, получим:
f	(x		) a					1				,
		0				1						,
f	(x		) a			2		2 1						,
		0				2								,
. . . . . .
f (k ) (x ) a										k (k 1) ... 2 1,
			0					k
. . . . . . . . . .
Значит, для коэффициентов ряда справедливы формулы:
															f			)					f (x		)							f	(k )	(x	)
a			f (x		)			,				a					0		,	a	2			0		, … ,			a	k				0
0				0				,					1			1!			,		2			2!		, … ,				k			k!
																1!								2!									k!

, … ,

т.е. данный ряд является рядом Тейлора этой функции. Теорема доказана. Замечание. Теорема единственности позволяет доказывать некоторые

тождества. Для этого раскладывают некоторую функцию двумя способами в степенной ряд. В силу теоремы единственности коэффициенты в обоих рядах при одинаковых степенях x совпадают.

4. Разложение основных элементарных функций.

Выпишем функций:

e	x	1 x
	x

разложения

x	2		x	n
		...			...
2!			n!

ряды Маклорена основных элементарных

x ( , ) ,

	x	3
sin x x	x
sin x x	3!
	3!

x	5

5!

... ( 1)	n

	x	2n 1

	(2n 1)!

...

x ( ,

)

	x	2
cos x 1	x
cos x 1	2!
	2!

x	4

4!

... ( 1)	n

	x	2n
	x
	(2n)!
	(2n)!

...

x ( , ) ,

ln(1 x) x

... ( 1)n 1

... ,

x ( 1,1],

(1 x)

1 x

( 1)

...

( 1)...( n 1)

...

Последнее разложение при 1 принимает вид:

1	1	x x 2	... ( 1)n x n ... ,	x ( 1,1) .

1 x

( 1,1)

Заменяя x на (-x), приходим к стандартной формуле для суммы геометрической прогрессии

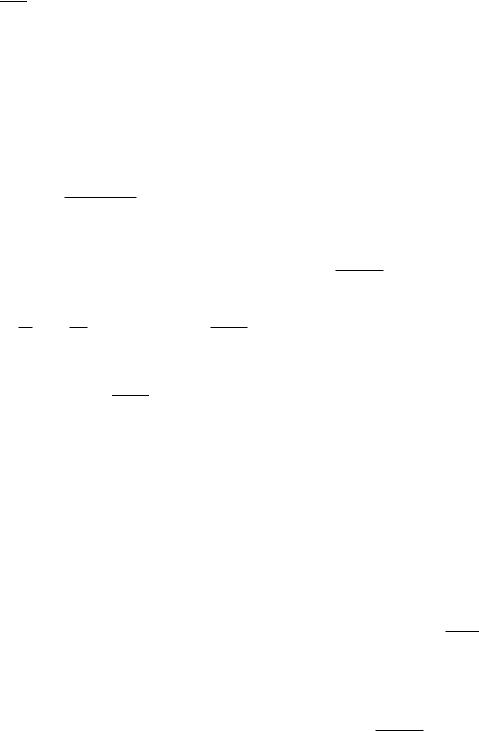
1−1 = 1 + + 2 + + + , (−1,1) .

5. Разложение функций в ряд Тейлора с использованием известных

разложений.

Пример 1. Разложить функцию	y sin	2	x	в ряд Маклорена.

производную n-го порядка в точке 0 = 0. Воспользуемся тригонометрическим тождеством:

sin2 x 1 cos2x , а затем табличным разложением функции

заменяя переменную x на переменную (2x):

		1	1		(2x)2	(2x)4
sin2	x			1			... ( 1)n
sin2	x			1			... ( 1)n
		2	2		2!	4!
		2	2		2!	4!

2		2	2	3		4		n 1	2	2n 1		2n
2	x		2		x		... ( 1)		2		x		...	,

2!			4!						(2n)!
2!			4!						(2n)!

В силу теоремы единственности имеем

(2x)2n (2n)!

x ( ,

...

)

Найти

cos x ,

22 −1

2 (0) = (−1) +1 ∙ (2 )! ∙ (2 )! = (−1) +1 ∙ 22 −1, 2 −1(0) = 0.

Пример 2. окрестности

Разложить функцию

точки	x	1	, т.е. по
	0


y ln(x	2	5x 6)	в ряд
y ln(x		5x 6)

степеням переменной				(x
степеням переменной

Тейлора в

1)	. Найти

производную n-го порядка в точке 0 = −1.

Пользуясь свойствами логарифмической функции, тождественные преобразования:

y ln(x	2	5x 6)	ln (x 2)(x 3) ln(x 2) ln(x 3)

				x 1
ln 1 (x 1) ln 2 (x 1) ln 2 ln 1 (x 1) ln 1
				2
а затем применим табличное разложение функции				ln(1

соответствующие замены:

выполним

x) , делая

	(x 1)	n		(x	1)		n
y ln 2 ( 1)n 1			( 1)n 1					ln 2

	n			2	n	n
n 1			n 1					n 1

( 1)n 1

1 n

1			n
		(x 1)		.
2	n	(x 1)		.
2

Чтобы найти значения x, для которых справедлива полученная формула, решим систему неравенств:

1 x 1 1

	x 1		1 x 1 1 2 x
1		1
1		1
	2

В силу теоремы единственности имеем (−1) =

0		.
		.
	(−1)−1		(1 +	1	) ∙ !.
			(1 +		) ∙ !.
				2

Пример 3. Разложить в ряд Маклорена функцию

arctg(x)

. Найти

производную n-го порядка в точке 0 = 0.

Воспользуемся табличным разложением для представления степенным рядом производной этой функции:

	y (arctg(x))	1
	y (arctg(x))	x
	1	x
		2

Тогда

1 x	2	x	4	...	( 1)	n	x	2n	...
	2		4			n		2n

( 1,1)

x		dx
arctg (x)
	1	x	2
0

	x	3	x	5
x x
	3		5

		x	2n 1
... ( 1)	n			...


		2n		1

, x [ 1,1] .

Заметим, что производная представляется степенным рядом на интервале

( 1,1) , а сама функция – на отрезке [ 1,1] .
В силу теоремы единственности имеем
2 +1(0) = (−1) ∙	1	∙ (2 + 1)! = (−1) ∙ (2 )!,	2(0) = 0.
	2+1

6. Приближенные вычисления значений функций и определенных

интегралов.

Рассмотрим примеры применения ряда Тейлора для приближенных

вычислений.
Пример 1. Вычислить 3
Пример 1. Вычислить 3															2 с точностью до 5 знаков после запятой.
Для решения								задачи							воспользуемся								табличным разложением																функции
				при						1		:

(1 x)										3
										3
									1				1	1					1	1	1	1		2
		1												1							1			2
		1				1																								1			1				5
(1 x)		3		1		1	x		3			3				x	2		3	3		3			x	3	... 1			1	x		1	x	2		5		x	3	...
						3							2!								3!									3			9			81					.
						3							2!								3!									3			9			81
																					1
			128		125					5			128				5			3		5			1			1						1
3																					3
3																					3
	2 3										3							1					1															... .
	2 3										3							1					1						2							2		... .
				64 125						4			125				4			125		4			125			(125)	2			75 (125)				2
				64 125						4			125				4			125		4			125			(125)				75 (125)

Последнее выписанное слагаемое этой суммы меньше, чем 10 5 . Кроме того, полученный числовой ряд является знакочередующимся рядом Лейбница, поэтому ошибка при замене суммы ряда на частичную сумму не превосходит по модулю первого отброшенного члена ряда. Значит, для достижения заданной точности достаточно учесть первые три члена ряда:

3	2

5	(1	0,008 0,000064)
4

1,25992	.

2 arctg(x)

Пример 2. Вычислить с точностью до 3 знаков после запятой dx .

0 x

Воспользуемся полученным разложением функции

arctg(x)

в ряд Маклорена:

1							1
2	arctg(x)						2			x	2
	arctg(x)									x
					dx
		x			dx			1		3
0		x					0			3
			x		x		x				1
			x	3	x	5	x	7		2
				3		5		7
x				2		2		2	...
			3	2	5	2	7	2
			3		5		7				0
											0

x	4			x	6
	4				6
							... dx
5				7
5				7
1				1					1					1
2		2	3	3		2		2	5	5	2	2	7		7	2
			3			2			5		2		7			2

...

Получен знакочередующийся ряд Лейбница, последнее выписанное

слагаемое меньше, чем				10	3	. Отбрасывая это слагаемое,
				10

приближенное значение интеграла с заданной точностью:
1
2	arctg(x)
	arctg(x)	dx 0,5	0,0138 0,0012 0,487				.
	x						.

0
0

получим

Соседние файлы в папке Лекции

#
25.12.2020572.77 Кб901.pdf
#
25.12.2020562.52 Кб802.pdf
#
25.12.2020407.81 Кб903.pdf
#
25.12.2020572.25 Кб804.pdf
#
25.12.2020425.76 Кб805.pdf
#
25.12.2020543.3 Кб706.pdf
#
25.12.2020581.83 Кб806 - презентация.pdf
#
25.12.2020428.79 Кб807.pdf
#
25.12.2020954.27 Кб807 - презентация.pdf
#
25.12.2020339.7 Кб808.pdf
#
25.12.2020610.96 Кб808 - презентация.pdf