Sbor_z_u_m (1)

4. Комплексные числа

В этом разделе мы познакомимся с понятием комплексного числа, рассмотрим

алгебраическую, тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня.

Для освоения комплексных чисел не требуется каких-то специальных знаний из курса высшей математики, и материал доступен даже школьнику. Достаточно уметь выполнять алгебраические действия с «обычными» числа, и помнить тригонометрию.

Сначала вспомним «обычные» Числа. В математике они называются множеством действительных чисел и обозначаются буквой R, либо R (утолщённой). Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой оси обязательно соответствует некоторое действительное число.

4.1. Понятие комплексного числа

«Комплексное число» - это не число в обычном понимании, характеризующееся одним параметром, а математический объект, составленный из двух элементов, каждый из которых - действительное число. Если хотите, комплексное число – двумерное число.

Геометрически комплексное число может быть представлено, как точка на плоскости (элемент плоскости), на которой задана прямоугольная система координат: две взаимно перпендикулярные числовые оси (0X и 0Y) с общей нулевой точкой (0) начала отсчёта. Произвольная точка такой координатной плоскости определяется упорядоченной парой чисел (x; y), где x и y называют обычно координатами точки по соответствующим осям. Пара называется упорядоченной, т. к. при перестановке чисел x≠y местами в скобках получается другое комплексное число (другая пара): (x; y) (y; x).

Определение: Всякое комплексное число представимо в виде упорядоченной пары действительных чисел: z = (x; y), где и x, и y – действительные числа, а z – «название» этой пары. Первое в паре число x = Re(z) называют действительной частью, а второе в паре число y = Im(z) – мнимой частью комплексного числа.

Определение: Алгебраическим представлением комплексного числа z называют «число» вида: z = a + b∙i. где a и b – действительные числа, а i - мнимая единица.

Действительные числа после этого определения стали обозначать, как x (x; 0), и отмечать их на числовой оси 0X, а мнимые числа (мнимые части комплексных чисел) – как y (0; y). Для комплексных чисел ввели особые алгебраические операции, и оказалось, что они представимы как в виде векторов, так и «алгебраически». Например, как: z = x + i∙y, если пару (комплексную величину) i (0; 1) назвать мнимой единицей.

73

Здесь действительное число a = Re(z) – действительная (реальная, real) часть z, а действительное число b = Im(z) - это мнимая (воображаемая, imagine) часть z.

А вот произведение числа b на упорядоченную пару (0; 1): b∙i = b∙(0; 1) = (0; b) является чисто мнимым числом.

Здесь a + b∙i – это обозначение единого комплексного числа, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить

местами: или переставить мнимую единицу: – от этого комплексное число не изменится.

Но стандартно в большинстве случаев комплексное число принято записывать именно в таком порядке: z = a + b∙i.

Чтобы всё было понятнее, приведём геометрическую интерпретацию. Комплексные числа изображаются в виде двумерных точек на комплексной плоскости:

Как упоминалось выше, буквой R принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой C. Поэтому на чертеже следует поставить букву C, обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость задаётся двумя осями:

X = Re(z) - действительная ось; Y = Im(z) – мнимая ось.

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать размерность (масштаб оси). Поэтому отмечаем точки:

ноль (0; 0)

единицу 1 по действительной оси (1; 0);

мнимую единицу i по мнимой оси (0; 1).

74

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Построим на комплексной плоскости следующие комплексные числа:

, ,

, ,

, , ,

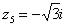По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось Re(z) обозначает в точности множество действительных чисел R, то есть на оси Re(z) сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел R является подмножеством множества комплексных чисел C.

Числа , , – это комплексные числа с нулевой мнимой частью.

75

Числа , , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси Im(z).

В числах 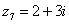, , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, так как что они сливаются с осями.

4.2. Алгебраическая форма комплексного числа. Алгебра комплексных чисел

Комплексное число, как упорядоченная пара чисел, представимо как в виде точки на комплексной плоскости, так и в виде z = a + bi, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще и

тригонометрическая, и показательная формы комплексного числа, о которых пойдет речь далее.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры. Необходимо только помнить, что алгебраические действия должны производиться одновременно с обеими частями упорядоченной пары.

Сложение комплексных чисел

Пример 1:

Сложить два комплексных числа , Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях. Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса: , – то есть «от перестановки слагаемых сумма не меняется».

Вычитание комплексных чисел

Пример 2:

Найти разности комплексных чисел и , если , Действие аналогично сложению, единственная особенность состоит в том, что

вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

.

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так:

.

Рассчитаем вторую разность:

76

изменилось, помножить числитель на то же самое число :

.

Далее в числителе нужно раскрыть скобки, т. е. перемножить два числа по правилу, рассмотренному в предыдущем пункте. А в знаменателе воспользоваться формулой

(помним, что i 2=-1, и не путаемся в знаках!!!). Распишем подробно:

Пример мы подобрали здесь «хороший», если же взять два числа «от балды», то в результате

деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим

частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы:

.

Для любителей упростить это частное приведём правильный ответ: i.

Пример 5:

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме a + bi).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу (a - b)(a + b) = a2 - b2. В знаменателе уже есть (a + b), поэтому знаменатель и числитель нужно помножить на сопряженное выражение (a - b), то есть

на :

Пример 6:

Даны два комплексных числа z1 = 5 + 2i, z2 = 2 – 5i. Найти их сумму, разность, произведение и частное. Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Иногда для решения предлагается навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что: i 2=-1.

78

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

Пример 7:

Представить в тригонометрической форме комплексные числа: , , , . Выполним чертёж:

На самом деле задание устное. Для наглядности перепишем тригонометрическую форму

комплексного числа:

Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол.

1) Представим в тригонометрической форме число . Найдем его модуль и аргумент.

Очевидно, что . Формальный расчет по формуле: . Очевидно, что (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: .

Ясно, как день, обратное проверочное действие: 2) Представим в тригонометрической форме число . Найдем его модуль и аргумент.

Очевидно, что .

80