Sbor_z_u_m (1)
.pdf
Пример 5
Найти предел 
Этот пример сложнее, попробуйте разобраться самостоятельно:
6.2.2. Второй замечательный предел
В теории математического анализа доказано, что:
Данный факт носит название второго замечательного предела.
Справка: 
– это иррациональное число.
В качестве параметра 
может выступать не только переменная 
, но и сложная функция.
Важно лишь, чтобы она стремилась к бесконечности.
Пример 6
Найти предел 
Когда выражение под знаком предела находится в степени – это первый признак того, что
нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 
.
Нетрудно заметить, что при 
основание степени 
, а показатель – 
, то есть имеется, неопределенность вида 
:
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в
данном примере параметр 
, значит, в показателе нам тоже нужно организовать 
. Для
131
этого возводим основание в степень 
, и, чтобы выражение не изменилось – возводим в степень 
:
Когда задание оформляется от руки, карандашом помечаем:
Практически всё готово, страшная степень превратилась в симпатичную букву 
:
При этом сам значок предела перемещаем в показатель.
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.
Пример 7
Найти предел 
Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.
Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:
В результате получена неопределенность 
. Но второй замечательный предел применим к неопределенности вида 
. Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас 
, значит, в числителе тоже нужно организовать 
:
Теперь можно почленно разделить числитель на знаменатель:
Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
132
Таким образом, основание приняло вид |
, и, более того, появилась нужная нам |
неопределенность 
. Организуем второй замечательный предел 
.
Легко заметить, что в данном примере 
. Снова исполняем наш искусственный прием:
возводим основание степени в 
, и, чтобы выражение не изменилось – возводим в обратную дробь 
:
Наконец-то долгожданное |
устроено, с чистой совестью превращаем его в букву : |
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида 
, раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на 
:
133
Готово.
А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй
замечательный предел выглядит следующим образом: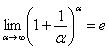 
. Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:
Пример 8
Найти предел 
Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в
выражение, стоящее под знаком предела:
В результате получена знакомая неопределенность 
. Очевидно, что в данном примере 
. С помощью знакомого искусственного приема организуем в показателе
степени конструкцию 
:
Выражение |
со спокойной душой превращаем в букву : |
Еще не всё, в показателе у нас появилась неопределенность вида 
. Раскладываем тангенс на синус и косинус (ничего не напоминает?):
134
Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:
А что такое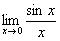 
и к чему оно стремится, нужно уже знать, иначе «двойка»!
Как видите, в практических заданиях на вычисление пределов нередко требуется применять сразу несколько правил и приемов.
В 90-95% на зачете, экзамене Вам встретится первый замечательный предел или второй замечательный предел. Как быть, если попался «экзотический» замечательный предел? (со списком всех замечательных пределов можно ознакомиться в соответствующей методичке). Ничего страшного, практически все выкладки, приёмы решения для первого замечательного предела справедливы и для остальных замечательных пределов. Нужно решать их по аналогии.
Да, так чему же равен предел 
?
Если у Вас получился ответ 
, значит в понимании высшей математики не всё так безнадежно = ).
7. Производные функций
Как найти производную, как взять производную? На данном уроке мы научимся находить производные функций. Но перед изучением данной страницы я настоятельно рекомендую ознакомиться с методическим материалом Горячие формулы школьного курса математики.
Справочное пособие можно открыть или закачать на страницеМатематические формулы и таблицы. Также оттуда нам потребуется Таблица производных, ее лучше распечатать, к ней часто придется обращаться, причем, не только сейчас, но и в оффлайне.
Есть? Приступим. У меня для Вас есть две новости: хорошая и очень хорошая. Хорошая новость состоит в следующем: чтобы научиться находить производные совсем не обязательно знать и понимать, что такое производная. Если Вас интересует теоретическое определение производной функции, математический, физический, геометрический смысл производной – поищите в Интернете, информации море. Наша же задача научиться находить эти самые производные. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.
7.1. Производные функций одной переменной.
Рекомендую следующий порядок изучения темы: во-первых, эта статья. Затем следует прочитать важнейший урок Производная сложной функции. Эти два базовых занятия позволят поднять Ваши навыки с полного нуля. Далее можно будет ознакомиться с более сложными производными в статье Сложные производные. Логарифмическая производная.
Если планка окажется слишком высока, то сначала прочитайте вещьПростейшие типовые задачи с производной. Помимо нового материала, на уроке рассмотрены другие, более
135
простые типы производных, и есть прекрасная возможность улучшить свою технику дифференцирования. Кроме того, в контрольных работах почти всегда встречаются задания на нахождение производных функций, которые заданы неявно или параметрически. Такой урок тоже есть: Производные неявных и параметрически заданных функций.
Я попытаюсь в доступной форме, шаг за шагом, научить Вас находить производные функций. Вся информация изложена подробно, простыми словами.
Собственно, сразу рассмотрим пример: Пример 1
Найти производную функции 
Решение: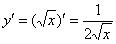 
Это простейший пример, пожалуйста, найдите его в таблице производных элементарных
функций. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь: у нас была функция 
, которая в результате решения превратилась в
функцию 
.
Говоря совсем просто, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением
является экспоненциальная функция 
, которая превращается сама в себя.Операция нахождения производной называется дифференцированием.
Обозначения: Производную обозначают 
или 
Вернемся к нашей таблице производных. Из данной таблицы желательно запомнить наизусть:
правила дифференцирования и производные некоторых элементарных функций, особенно: производную константы:
, где 
– постоянное число; производную степенной функции:
, в частности: 
, 
, 
.
Зачем запоминать? Данные знания являются элементарными знаниями о производных. И если Вы не сможете ответить преподавателю на вопрос «Чему равна производная числа?», то учеба в ВУЗе может для Вас закончиться (лично знаком с двумя реальными случаями из жизни).
Кроме того, это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда мы сталкиваемся с производными.
В реальности простые табличные примеры – редкость, обычно при нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.
7.1.1. Правила дифференцирования:
1) Постоянное число можно (и нужно) вынести за знак производной
, где 
– постоянное число (константа) Пример 2
Найти производную функции 
Смотрим в таблицу производных. Производная косинуса там есть, но у нас 
. Решаем:
136
Самое время использовать правило, выносим постоянный множитель за знак производной:
А теперь превращаем наш косинус по таблице:
Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:
Готово.
2) Производная суммы равна сумме производных
Пример 3
Найти производную функции 
Решаем. Как Вы, наверное, уже заметили, первое действие, которое всегда выполняется при
нахождении производной, состоит в том, что мы заключаем в скобки всё выражение и ставим штрих справа вверху:
Применяем второе правило:
Обратите внимание, что для дифференцирования все корни, степени нужно представить в
виде 
, а если они находятся в знаменателе, то переместить их вверх. Как это сделать – рассмотрено в моих методических материалах.
Теперь вспоминаем о первом правиле дифференцирования – постоянные множители (числа) выносим за знак производной:
Обычно в ходе решения эти два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).
Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:
137
Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:
Все степени вида 
желательно снова представить в виде корней, степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет. Пример 4
Найти производную функции 
Попробуйте решить данный пример самостоятельно (ответ в конце урока)
3) Производная произведения функций
Вроде бы по аналогии напрашивается формула 
…., но неожиданность состоит в том, что:
Я не буду объяснять, почему именно так, наша задача научиться решать производные, а не разбираться в теории.
Пример 5
Найти производную функции 
Здесь у нас произведение двух функций, зависящих от 
.
Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:
138
Сложно? Вовсе нет, вполне доступно даже для чайника. Пример 6
Найти производную функции 
В данной функции содержится сумма 
и произведение двух функций – квадратного
трехчлена 
и логарифма 
. Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.
Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:
Теперь для скобки |
используем два первых правила: |
В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции:
Готово.
При определенном опыте нахождения производных, простые производные вроде 
не обязательно расписывать так подробно. Вообще, они обычно решаются устно, и сразу
записывается, что 
. Пример 7
Найти производную функции 
Это пример для самостоятельного решения (ответ в конце урока)
4) Производная частного функций
В потолке открылся люк, не пугайся, это глюк. А вот это вот суровая действительность:
Пример 8
Найти производную функции 
Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть
сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:
139
Теперь смотрим на выражение в скобках, как бы его упростить? В данном случае замечаем множитель, который согласно первому правилу целесообразно вынести за знак производной:
Заодно избавляемся от скобок в числителе, которые теперь не нужны.
Вообще говоря, постоянные множители при нахождении производной можно и не выносить, но в этом случае они будут «путаться под ногами», что загромождает и затрудняет решение. Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И здесь – сначала применяем правило дифференцирования частного:
Таким образом, наша страшная производная свелась к производным двух простых выражений. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:
Штрихов больше нет, задание выполнено.
На практике обычно (но не всегда) ответ упрощают «школьными» методами:
Пример 9
Найти производную функции 
Это пример для самостоятельного решения (ответ в конце урока).
Время от времени встречаются хитрые задачки: Пример 10
140