
Sbor_z_u_m (1)
.pdf
Поскольку  (случай 3), то
(случай 3), то
. Таким образом:
– число  в тригонометрической форме.
в тригонометрической форме.
Пример 11: Решение:
Представим число в тригонометрической форме:  (это число
(это число  Примера 8). Используем формулу Муавра
Примера 8). Используем формулу Муавра 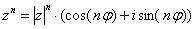 :
:
Пример 13: Решение:
Пример 15: Решение:
 ,
, 
Разложим квадратный двучлен на:
91

5. Математические формулы и графики
5.1. Математические формулы
Прежде, чем Вы приступите к изучению наших методических материалов, да и вообще приступите к изучению любых материалов по высшей математике, НАСТОЯТЕЛЬНО РЕКОМЕНДУЕМ прочитать нижеследующее.
Для того чтобы успешно решать задачи по высшей математике НЕОБХОДИМО:
– Уметь складывать, вычитать, умножать и делить. Вспомнить, что любая дробь, например
 , обозначает деление, «три делить на семь» в данном случае. Вспомнить, что такое
, обозначает деление, «три делить на семь» в данном случае. Вспомнить, что такое
квадратный корень, например:  .
.
ЗАПАСИТЕСЬ КАЛЬКУЛЯТОРОМ, ещё лучше - научитесь умножать и делить многозначные числа «столбиком».
Есть? Уже хорошо.
– От перестановки слагаемых – сумма не меняется:  .
.
А вот это - совершенно разные вещи:
Переставлять «икс» и «четверку» просто так нельзя. Заодно вспоминаем культовую букву «икс», которая в математике обозначает неизвестную или переменную величину.
– От перестановки множителей – произведение не меняется:  .
.
С делением такой фокус не пройдет,  и
и  – это две совершенно разные дроби и перестановка числителя со знаменателем без последствий не обходится.
– это две совершенно разные дроби и перестановка числителя со знаменателем без последствий не обходится.
Также вспоминаем, что знак умножения («точкy») чаще принято не писать:  ,
,  .
.
– Вспоминаем правила раскрытия скобок:
 – здесь знаки у слагаемых не меняются
– здесь знаки у слагаемых не меняются
 – а здесь меняются на противоположные. И для умножения:
– а здесь меняются на противоположные. И для умножения:
Вообще, достаточно помнить, что ДВА МИНУСА ДАЮТ ПЛЮС, а ТРИ МИНУСА – ДАЮТ МИНУС. И, постараться при решении задач по высшей математике в этом НЕ ЗАПУТАТЬСЯ (очень частая и досадная ошибка).
92

–Вспоминаем приведение подобных слагаемых, Вы должны хорошо понимать, что следующее действие:
–это всего лишь обычное сложение.
–Вспоминаем, что такое степень:
 ,
,  ,
,  ,
,  .
.
Степень - это, что дроби можно сокращать: 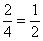 (сократили на 2),
(сократили на 2),  (сократили на пять),
(сократили на пять),  (сократили на
(сократили на  ).
).
– Вспоминаем действия с дробями: 
а также, очень важное правило приведения дробей к общему знаменателю:
Если данные примеры малопонятны, смотрите школьные учебники. Без этого ТУГО
будет.
СОВЕТ: все ПРОМЕЖУТОЧНЫЕ вычисления в высшей математике лучше проводить в ОБЫКНОВЕННЫХ ПРАВИЛЬНЫХ И НЕПРАВИЛЬНЫХ ДРОБЯХ, даже если будут
получаться страшные дроби вроде  . Вот эту вот дробь НЕ НАДО представлять в виде
. Вот эту вот дробь НЕ НАДО представлять в виде
 , и, тем более, НЕ НАДО делить на калькуляторе числитель на знаменатель, получая
, и, тем более, НЕ НАДО делить на калькуляторе числитель на знаменатель, получая
4,334552102….
ИСКЛЮЧЕНИЕМ из правила является конечный ответ задания, вот тогда как раз лучше записать  или
или  .
.
93

– Уравнение. У него есть левая часть и правая часть. Например:
 ,
,
то можно перенести любое слагаемое в другую часть, сменив у него знак: Перенесем,
например, все слагаемые в левую часть:  Или в правую:
Или в правую:
Обратите внимание, что можно безболезненно переставить части уравнения местами:
 , а равно, как и перетасовать слагаемые в пределах
, а равно, как и перетасовать слагаемые в пределах
ОДНОЙ части.
– Правило пропорции:
 ,
,  ,
,  ,
, 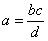 ,
,  ,
,  ,
,  – это одно и то же.
– это одно и то же.
То, что находится внизу одной части – можно переместить наверх другой части.
То, что находится вверху одной части – можно переместить вниз другой части.
– И, наконец, стОит вспомнить о существовании некоторых функций. Таких, как синус,
косинус, тангенс, котангенс и логарифм. При этом в качестве аргумента функции может выступать не только буковка «хэ» (например,  ), но и сложное выражение, например
), но и сложное выражение, например
 , и, рвать функцию на части категорически нельзя!
, и, рвать функцию на части категорически нельзя!
Не лишним будет вспомнить графики основных функций, предаться воспоминаниям можно на странице Графики и свойства элементарных функций. Там же освежаем в памяти актуальный технический вопрос – Как правильно построить график любой функции?
Вот, пожалуй, и все основные вещи школьного курса математики, которые нужно помнить. Если какие-либо моменты непонятны, или понятны смутно, отсылаю Вас к школьным учебникам по математике. Перед решением заданий по высшей математике весьма полезно ознакомиться со справочным материалом Горячие формулы высшей математики.
Далее методический материал представляет собой обзор графиков основных элементарных функций и их свойств. Будет полезен при изучении практически всех разделов высшей математики, более того, поможет вам лучше и качественнее разобраться в некоторых темах. Также вы сможете узнать, какие значения функций следует знать наизусть, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Содержит много графиков функций, которые также желательно помнить.
94

5.2. Графики и основные свойства элементарных функций
Данный методический материал носит справочный характер и его нельзя отнести к какой-либо определенной теме. В статье приведен обзор графиков основных элементарных функций и рассмотрен важнейший вопрос – как правильно и БЫСТРО построить график. В ходе изучения высшей математики без знания графиков основных элементарных функций придётся тяжело, поэтому очень важно вспомнить, как выглядят графики параболы, гиперболы, синуса, косинуса и т.д., запомнить некоторые значения функций. Также речь пойдет о некоторых свойствах основных функций.
Мы не претендуем на полноту и научную основательность материалов, упор будет сделан, прежде всего, на практику – тех вещах, с которыми приходится сталкиваться буквально на каждом шагу, в любой теме высшей математики. Графики для чайников?
Можно сказать и так.
Как правильно построить координатные оси?
На практике контрольные работы почти всегда оформляются студентами в отдельных тетрадях, разлинованных в клетку. Зачем нужна клетчатая разметка? Ведь работу, в принципе, можно сделать и на листах А4. А клетка необходима как раз для качественного и точного оформления чертежей.
Любой чертеж графика функции начинается с координатных осей.
Чертежи бывают двухмерными и трехмерными.
Сначала рассмотрим двухмерный случай декартовой прямоугольной системы координат:
1)Чертим координатные оси. Чертить всегда стараемся аккуратно и не криво. Стрелочки тоже не должны быть похожи на бороду Папы Карло.
2)Подписываем оси. Не забываем подписывать оси.
3)Задаем размерность по осями: рисуем ноль и две единички. При выполнении чертежа самая удобная и часто встречающаяся размерность: 1 единица = 2 клеточки (чертеж слева). Я рекомендую Вам по возможности всегда придерживаться именно такой размерности. Но, время от времени случается так, что чертеж не вмещается на тетрадный лист – тогда размерность уменьшаем: 1 единица = 1 клеточка (чертеж справа). Редко-редко, но бывает, что размерность чертежа приходиться уменьшать (или увеличивать) еще больше.
95

НЕ НУЖНО по осям проставлять все значения: …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, …. Ибо координатная плоскость – не памятник Лобачевскому, а студент – не голубь. Ставим ноль и две единицы по осям. Как говорят математики, это необходимо и достаточно. Размерность можно задать и произвольно, например, поставить 0 и – 1, –1 – по осям, но существуют некоторые стандарты, которых целесообразно придерживаться.
Предполагаемые размеры чертежа лучше оценить еще ДО построения чертежа. Так,
например, если в задании требуется начертить треугольник с вершинами  ,
,  ,
,  , то совершенно понятно, что популярная размерность 1 единица = 2 клеточки не
, то совершенно понятно, что популярная размерность 1 единица = 2 клеточки не
подойдет. Почему? Посмотрим на точку  – здесь придется отмерять пятнадцать сантиметров вниз, и, очевидно, что чертеж не вместится (или вместится еле-еле) на тетрадный лист. Поэтому сразу выбираем меньшую размерность 1 единица = 1 клеточка.
– здесь придется отмерять пятнадцать сантиметров вниз, и, очевидно, что чертеж не вместится (или вместится еле-еле) на тетрадный лист. Поэтому сразу выбираем меньшую размерность 1 единица = 1 клеточка.
Кстати, о сантиметрах и тетрадных клетках. Правда ли, что в 30 тетрадных клетках содержится 15 сантиметров? Отмерьте в тетради для интереса 15 сантиметров линейкой. В
СССР, возможно, это было правдой… Интересно отметить, что если отмерить эти самые сантиметры по горизонтали и вертикали, то результаты (в клетках) будут разными! Строго говоря, современные тетради не клетчатые, а прямоугольные. Возможно, это покажется ерундой, но, чертить, например, окружность циркулем при таких раскладах очень неудобно.
К слову о качестве, или краткая рекомендация по канцтоварам. На сегодняшний день большинство тетрадей в продаже, плохих слов не говоря, - это полное безобразие. По той причине, что они промокают, причём не только от гелевых, но и от шариковых ручек! На бумаге экономят. Для оформления контрольных работ рекомендую использовать тетради Архангельского ЦБК (18 листов, клетка) или «Пятёрочку», правда, она дороже. Ручку желательно выбрать гелевую, даже самый дешевый китайский гелевый стержень намного лучше, чем шариковая ручка, которая - то мажет, а то дерёт бумагу. Единственной «конкурентоспособной» шариковой ручкой на моей памяти является «Эрих Краузе». Она пишет чётко, красиво и стабильно – что с полным стержнем, что с практически пустым. Немецкое качество.
Трехмерный случай
Здесь почти всё так же.
1)Чертим координатные оси. Стандарт: ось  – направлена вверх, ось
– направлена вверх, ось  – направлена вправо, ось
– направлена вправо, ось  – влево вниз строго под углом 45 градусов.
– влево вниз строго под углом 45 градусов.
2)Подписываем оси.
96

3) Задаем размерность по осям. Размерность по оси OX – в два раза меньше, чем размерность по другим осям. Также обратите, внимание, что на правом чертеже размерность задана нестандартно – по оси OX двойкой, а не единицей. С нашей точки зрения, так точнее, и, главное, быстрее и удобнее – не нужно под микроскопом выискивать середину клеточки.
При выполнении трехмерного чертежа опять же желательно придерживаться размерности 1 единица = 2 клеточки (чертеж слева).
Для чего существует эти правила? Правила, как известно, существуют для того, чтобы их нарушать! Чем я сейчас и займусь. Дело в том, что все последующие чертежи статьи будут выполнены мной в Экселе, и, координатные оси будут выглядеть некорректно с точки зрения правильного оформления. Можно было бы начертить все графики от руки, но MS Excel их начертит гораздо точнее.
График линейной функции
Линейная функция задается уравнением  . График линейной функций представляет собой прямую линию. Для того, чтобы построить прямую, достаточно знать две точки.
. График линейной функций представляет собой прямую линию. Для того, чтобы построить прямую, достаточно знать две точки.
Пример 1
Построить график функции  . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
. Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
Если  , то
, то 
Берем еще какую-нибудь точку, например, 1.
Если  , то
, то 
При оформлении заданий координаты точек обычно сводятся в таблицу:
А сами значения рассчитываются устно или на черновике, калькуляторе.
Две точки найдены, выполним чертеж:
97

При оформлении чертежа всегда подписываем графики.
Не лишним будет вспомнить частные случаи линейной функции:
98

Обратите внимание, как расположены подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было постаить
подпись рядом с точкой пересечения |
прямых |
, |
или |
справа внизу между |
|
графиками. |
|
|
|
|
|
1) Линейная функция вида |
( |
) |
выражает |
прямую |
пропорциональную |
зависимость. Например,  . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
2) Уравнение вида  задает прямую, параллельную оси
задает прямую, параллельную оси  , в частности, сама ось
, в частности, сама ось  задается уравнением
задается уравнением  . График функции строится сразу, без нахождения всяких точек.
. График функции строится сразу, без нахождения всяких точек.
То есть, запись  следует понимать так: «игрек всегда равен –4, при любом значении икс».
следует понимать так: «игрек всегда равен –4, при любом значении икс».
3) Уравнение вида  задает прямую, параллельную оси
задает прямую, параллельную оси  , в частности, сама ось
, в частности, сама ось 
задается уравнением  . График функции также строится сразу. Запись
. График функции также строится сразу. Запись  следует понимать так: «икс всегда, при любом значении игрек, равен 1».
следует понимать так: «икс всегда, при любом значении игрек, равен 1».
Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения
графика вроде 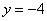 или
или  .
.
Построение прямой – самое распространенное действие при выполнении чертежей.
99

График квадратичной, кубической функции, график многочлена
Парабола. График квадратичной функции  (
( ) представляет собой параболу. Рассмотрим канонический случай:
) представляет собой параболу. Рассмотрим канонический случай: 
Вспоминаем некоторые свойства функции  .
.
Область определения этой функции – любое действительное число. Какую бы точку на оси  мы не выбрали – для каждого «икс» существует значение функции
мы не выбрали – для каждого «икс» существует значение функции  . Область
. Область
определения стандартно обозначается как  , или
, или  . В данном случае область определения – все множество действительных чисел D(y) = R.
. В данном случае область определения – все множество действительных чисел D(y) = R.
Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае это  – множество всех положительных значений, включая ноль. Область значений стандартно обозначается как
– множество всех положительных значений, включая ноль. Область значений стандартно обозначается как  , или
, или  .
.
Функция 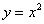 является чётной. Если функция является чётной, то ее график
является чётной. Если функция является чётной, то ее график
симметричен относительно оси  . Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции
. Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции
выражается условием |
. Как проверить любую функцию на чётность? Нужно |
||
вместо |
подставить в уравнение |
. В случае с параболой проверка выглядит так: |
|
 , значит, функция
, значит, функция 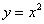 является четной.
является четной.
Функция  не ограничена сверху. Аналитически свойство записывается так:
не ограничена сверху. Аналитически свойство записывается так:
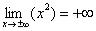 . Вот вам, кстати, и пример геометрического смысла предела функции: если мы
. Вот вам, кстати, и пример геометрического смысла предела функции: если мы
будет уходить по оси  (влево или вправо) на бесконечность, то ветки параболы (значения «игрек») будут неограниченно уходить вверх на «плюс бесконечность». При изучении пределов функций желательно понимать геометрический смысл предела.
(влево или вправо) на бесконечность, то ветки параболы (значения «игрек») будут неограниченно уходить вверх на «плюс бесконечность». При изучении пределов функций желательно понимать геометрический смысл предела.
Пример 2
100
