Физика_лек_pdf / Модуль 8. Геометрическия оптика и фотометрия

ГЕОМЕТРИЧЕСКАЯ ОПТИКА И ФОТОМЕТРИЯ

Тема 1. Элементы геометрической оптики

Эволюция представлений о природе света

Опытные представления о свете сформулировались к концу XVII века в корпускулярную и волновую теории света.

Корпускулярная теория разработана И. Ньютоном. Свет, испускаемый светящимся телом, по данной теории представляет собой поток частиц, называемых еще корпускулами. Корпускулы имеют разные размеры. Красному свету соответствуют частицы наибольшего, а фиолетовому — наименьшего размера. Прямолинейное движение корпускул света И. Ньютон описал предложенными им же законами механики. С помощью корпускулярной теории И. Ньютон объяснил явление дисперсии. Однако дать объяснение интерференции, дифракции и других оптических явлений данная теория не смогла.

Волновая теория разработана X . Гюйгенсом, Р. Гуком и Ж. Френелем на основе аналогии оптических и акустических явлений. По этой теории свет представляет собой упругую волну, которая, естественно, способна распространяться только в упругом эфире. Основой волновой теории является принцип Гюйгенса-Френеля, согласно которому, как известно, каждая точка фронта волны служит источником вторичных волн. Наиболее наглядно волновые свойства света обнаруживаются в явлениях интерференции и дифракции. Обе теории в свое время убедительно объясняли закономерности прямолинейного распространения, отражения и преломления света.

До конца XIX века предпочтение отдавалось теории Ньютона. В дальнейшем большее признание получила волновая теория. Но и теория Гюйгенса имела ряд недостатков. Например, с ее помощью невозможно обосновать физическую природу многокомпонентности белого свеса. А слабым местом волновой теории вообще являлся гипотетический « мировой эфир».

Дальнейшее развитие идеи волновой природы света имело место в 70-е годы прошлого столетия в электромагнитной теории Дж. Максвелла. Однако представление о свете, как об электромагнитной волне, по-прежнему базировалось на существовании «мирового эфира» и не смогло раскрыть сущности механизма процессов испускания и поглощения света, фотоэлектрического эффекта и зависимости показателя преломления от длины волны. Теория Максвелла имела прежний для волновой теории недостаток — она была построена с использованием модели упругого мирового эфира.

Физическое толкование явления дисперсии света было дано Г. Лоренцом в конце XIX столетия. Созданная им теория получила название электронной. По сути Г. Лоренц всего лишь уточнил теорию Дж. Максвелла тем, что установил зависимость длины волны падающего света от диэлектрической проницаемости среды. Электронная теория, как и электромагнитная, оказалась неспособной охарактеризовать эффекты взаимодействия света с веществом, и, в частности, вопроса о распределении энергии по длинам волн при тепловом излучении абсолютно черного тела.

Противоречия волновой и корпускулярной теорий и затруднения каждой из них были устранены гипотезой М. Планка, высказанной в 1900 г. По гипотезе М. Планка излучение атомом электромагнитных волн происходит не непрерывно, а дискретно. Иными словами, оно происходит определенными порциями — квантами, энергия которых пропорциональна частоте v , с– 1 :

ε = hv , Дж, (17.1)

где h = 6,626 ∙ 10– 34 Дж ∙ с — постоянная Планка. Гипотеза М. Планка сделала возможным количественное описание процесса теплового излучения абсолютно черного тела. Кроме того, гипотеза не нуждалась в гипотетическом эфире.

Используя понятие кванта энергии. А. Эйнштейн в 1905 г. предложил квантовую теорию света. Согласно теории не только излучение, но и поглощение света, а также его распространение происходят в виде потока световых квантов-фотонов, энергия которых определяется предыдущим уравнением, а масса

т ф = ε /с2 = hv / c 2 = h /( λc ), кг. (17.2)

Квантовые представления о свете удовлетворяют законам излучения и поглощения света, взаимодействия света с веществом. явления интерференции и дифракции легко объясняются волновыми свойствами света и описываются волновой теорией. В других явлениях: фотоэффекте, люминесценции, в атомных и молекулярных спектрах, обнаруживаются корпускулярные свойства. Таким образом, все оптические явления описываются квантовой теорией, которая объединяет волновые и корпускулярные свойства света и не использует понятие эфира. Вся сложность восприятия теории и обусловлена этим единством противоположных форм движения — корпускулярной (квантовой) и волновой (электромагнитной).

Таким образом, современное представление о свете связано с его двойственной корпускулярно-волновой природой. Уравнения (17.1) и (17.2) отражают связь корпускулярных характеристик излучения (массы и энергии кванта), с волновыми — частотой колебаний и длиной волны. Для конкретного компонента видимого света частота излучения всегда постоянна, тогда как соответствующая ей длина волны зависит от фазовой скорости света v = с (εμ)– 0,5 м/с, в данной среде. При переходе света из одной среды в другую частота его не меняется, и следовательно, сохраняется его цвет, а длина волны меняется.

То, что свет представляет собой единство свойств дискретности и непрерывности, не противоречит выводам диалектического мировоззрения.

Основные понятия геометрической оптики

Рассмотрим наиболее часто встречающиеся в дальнейшем общие понятия и характеристики света:

1.Оптически однородной — изотропной, называют среду, по всем направлениям которой скорость распространения света одинакова.

2.Монохроматическим называют излучение, которому соответствует фиксированная длина волны.

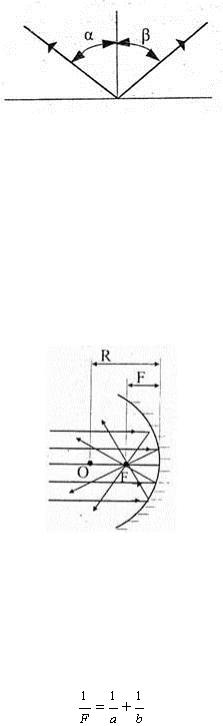
3. На границе раздела двух сред с различной оптической плотностью свет частично отражается, а частично проходит, преломляясь, во вторую среду. Падающий и отраженный лучи лежат в одной плоскости с перпендикуляром, проведенным к границе раздела сред в точке падения (рис. 17.1). При этом угол падения α равен углу отражения β

— закон отражения. Отражающая поверхность может быть зеркальной (идеализированное понятие) или шероховатой.

Рис. 17.1

Закон отражения справедлив также для неплоских поверхностей. В этом случае в разных точках поверхности зеркала перпендикуляр имеет различные направления. Вогнутое зеркало может быть сферическим или параболическим. Во втором случае оно представляет собой часть параболоида вращения. Лучи, падающие на поверхность вогнутого зеркала параллельно оптической оси, отражаются от него и собираются в фокусе F (рис. 17.2) на расстоянии, равном половине радиуса кривизны поверхности зеркала и называемым фокусным расстоянием вогнутого зеркала

F = 0,5R , м.

Рис. 17.2

Для построения изображения в вогнутом зеркале необходимо воспользоваться двумя из трех лучей, указанных на рис. 17.3. Из рисунка очевидна количественная зависимость между фокусным расстоянием F вогнутого зеркала, расстоянием а от предмета до зеркала и расстоянием b от зеркала до изображения

Рис. 17.3

Из рисунка также следует, что размеры предмета и его изображения находятся в следующей зависимости от расстояний их до зеркала:

т /п = а / b

Падающий и преломленный лучи лежат в одной плоскости с перпендикуляром, проведенным к границе раздела сред в точке падения (рис. 17.4). При этом отношение синуса угла падения к синусу угла преломления равно отношению фазовых скоростей света в первой и во второй средах — закон преломления:

sinα/sinγ = v 1 /v 2 . (17.3)

Рис. 17.4

Если v 1 = с , а v 2 = v , то согласно (17.3) sinα/sinγ = c /v .

4. Абсолютным показателем преломления называют оптическую характеристику среды, которая показывает, во сколько раз фазовая скорость света в данной среде меньше

скорости света в вакууме: где ε и μ — соответственно диэлектрическая и магнитная проницаемости среды. Абсолютный показатель преломления газов разной атомности незначительно больше единицы. Для жидкостей он находится в интервале от 1,2 до 1,9, а для твердых тел — в интервале 1,3–4. Показатель преломления вакуума равен единице. С учетом изложенного закон преломления можно записать в виде

sin α /sin γ = v 1 /v 2 = cv 1 /cv 2 = n 1 /n 2 = n 21 .

где n 21 = n 1 / n 2 — относительный показатель преломления второй среды относительно первой.

5.Среду с большим показателем преломления называют оптически более плотной, а среду с меньшим показателем —оптически менее плотной.

6.Атмосфера Земли оптически неоднородна. С увеличением высоты показатель преломления ее непрерывно уменьшается. Световой луч в атмосфере проходит как бы через множество тонких, параллельных друг другу, слоев. В результате луч света в атмосфере искривляется. Это явление называют рефракцией света в атмосфере. При рефракции искривление светового луча может достигать таких значений, при которых становятся видимыми объекты, находящиеся за горизонтом.

Рефракция отсутствует для лучей, идущих от объекта, находящегося в зените. Однако при смещении объекта из наивысшего положения она возникает и увеличивается по мере приближения объекта к линии горизонта. Уже в средние века было известно, что рефракция света приводит к возрастанию длительности дневной части суток.

Рефракцией световых лучей в атмосфере объясняется и сплюснутость заходящего Солнца по вертикали. В момент, когда нижний край Солнца касается линии горизонта, вертикальный диаметр солнечного диска виден земному наблюдателю под углом 26', а горизонтальный — по прежнему под углом 32'. Уменьшение вертикального размера на 6' является кажущимся, так как, наблюдая касание нижнего края светила линии горизонта, зритель не сознает, что в действительности весь солнечный диск находится уже за горизонтом.

Солнечный диск у горизонта кажется более крупным, чем в зените. Но это всего лишь оптическая иллюзия, так как углы, под которыми виден диск Солнца в зените и у горизонта, — одни и те же. Наиболее простым и естественным объяснением этому явлению представляется следующее. Иллюзия увеличения размеров заходящего Солнца обусловлена психологией нашего восприятия размеров объектов, наблюдаемых вначале в далекой перспективе, а затем в кажущемся приближении. Приближение Солнца к линии горизонта кажется наблюдателю приближением к нему. По этой причине Солнце воспринимается нашим сознанием преувеличенно большим несмотря на то, что видится оно все так же под углом 32'.

Рис. 17.5

7. При прохождении света из оптически более плотной среды с показателем преломления n 1 в оптически менее плотную среду с n 2 < n 1 (рис. 17.5) согласно предыдущему уравнению (17.3) α < γ. При некотором угле падения α = αпр , называемом предельным, угол преломления окажется равным 90° — преломленный луч будет скользить вдоль границы раздела сред sin αпр / sin 90° = n 21 . При α > αпр свет полностью в отражается в первую среду. Это явление называют полным отражением света.

9. При прохождении через призму свет раскладывается на компоненты с различными длинами волн. Такое явление называют дисперсией света. В более широком смысле под дисперсией света понимают разложение света в спектр, происходящее при его преломлении. Дисперсия также сопутствует интерференции и дифракции. Причина этого явления состоит в том, что угол преломления γ зависит от фазовой скорости излучения в среде призмы. Действительно, поскольку в средах с различной оптической плотностью фазовая скорость света будет разной, так как для конкретной составляющей видимого света частота излучения всегда постоянна, то из общего уравнения v = λ v следует, что длина волны рассматриваемого излучения при переходе из одной среды в другую также будет меняться. Если повторить это же рассуждение применительно к одной среде (в данном случае — призме, и нескольким излучениям с различной длиной волны), то понятно, что скорости их будут также различными и прямо пропорциональными длине волны.

Из известного равенства sinα / sinγ = c / v = n на основании изложенного sinα = const , с = const и v = var и, следовательно, sinγ и показатель преломления п также будут переменными. То есть будет иметь место преломление составляющих света под углами, пропорциональными фазовой скорости излучения.

При разложении белого света возникает цветовая полоса, называемая спектром. Отдельные цвета этой полосы называют спектральными цветами. Смена цветов происходит постепенно. Разделение спектра на цвета условно. Каждому цвету соответствует определенный интервал длин волн:

В зависимости от свойств источника света различают сплошные, линейчатые и полосатые спектры. В сплошном спектре представлены все длины волн с постепенным переходом от одного цвета к другому. Сплошной спектр дают нагретые твердые тела и жидкости.

Линейчатый спектр состоит из ряда резко очерченных цветных линий. Каждой из них соответствует конкретная длина световой волны. Цветные линии разделены широкими темными промежутками. Спектр характерен для нагретых одноатомных разреженных газов (инертные газы, пары металлов, диссоциированные многоатомные газы).

Полосатый спектр состоит из большого числа цветных линий, расположенных отдельными группами. В каждой группе линии сближены настолько, что группа представляется отдельной полосой. Каждой полосе спектра соответствует некоторый интервал длин волн. Полосатый или селективный спектр характерен для нагретых многоатомных разреженных газов (кислорода, диоксида углерода, водяного пара и др.).

10. Каждому химическому элементу принадлежит строго определенный спектр излучения, характеризуемый числом спектральных линий, их цветом и взаимным расположением. На этом основан спектральный анализ химического состава вещества. По закону Г. Кирхгофа газы поглощают только те линии спектра, которые они сами излучают.

Наиболее изученным спектром поглощения является солнечный спектр. При прохождении солнечного света через газовую оболочку возникают многочисленные линии поглощения, которые, называются фраунгоферовыми линиями.

11. При прохождении света через плоскопараллельную пластину преломление происходит на верхней и нижней границах (рис. 17.8). Луч при этом не меняет направления распространения, а только смещается параллельно самому себе на величину

Рис 17.8

12.Для изменения направления световых лучей в оптических приборах используют линзы. Это прозрачные со сферическими поверхностями тела. Двояковыпуклые линзы являются собирающими, а двояковогнутые — рассеивающими. Фокусом линзы называют точку, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.

13.Главной оптической осью линзы называют прямую, проходящую через главный оптический центр линзы и центр кривизны поверхности, образующей линзу.

14.Побочной оптической осью называют любую прямую, проходящую под углом к главной оптической оси через оптический центр линзы. Луч, идущий по главной или побочной оптической оси, называют центральным.

Оптические приборы предназначены для:

1.Получения изображений — фотоаппараты, проекционные аппараты и т.д.;

2.Увеличения угла зрения — лупы, подзорные трубы, микроскопы, телескопы и т.д.

Кроме отдельных оптических приборов используются сложные оптические системы специального назначения, например, для программы СОИ и в авиации.

Цит. по: Физика: учебник / Демидченко В.И. — Ростов н/Д: Феникс, 2006. — С. 352–360.

Преломление в линзе. Общая формула линзы

Большое значение имеет простейший случай центрированной системы, состоящей всего из двух сферических поверхностей, ограничивающих какой-либо прозрачный хорошо преломляющий материал (обычно стекло) от окружающего воздуха. Такая система представляет, очевидно, обычную линзу .

или, вводя относительный показатель преломления N = п /n 1

Эта общая формула линзы годна для линз выпуклых и вогнутых при любом расположении источника и соответствующем расположении фокуса. Нужно только принять во внимание знаки а 1 , а 2 , R 1 , R 2 , считая их положительными, если они отложены вправо от линзы, и отрицательными, если они отложены влево от линзы ). Если знаки а 1 и a 2 одинаковы, то одна из сопряженных точек — мнимая, т.е. в ней пересекаются не сами лучи, а их воображаемые продолжения.

Фокусные расстояния тонкой линзы

Если светящаяся точка, лежащая на главной оси, удаляется от линзы (а 1 возрастает по абсолютной величине), то изображение перемещается. Положение изображения, соответствующее предельному случаю, когда источник удален в бесконечность, носит название фокуса линзы. Таким образом, фокус есть точка, сопряженная бесконечно удаленной точке главной оси, или, что то же, — место схождения лучей, параллельных главной оптической оси. Расстояние от линзы до фокуса есть фокусное расстояние тонкой линзы. Плоскость, проходящая через фокус перпендикулярно к главной оси,

называется фокальной плоскостью .

Если лучи идут из бесконечности параллельным пучком, но под углом к главной оси (вдоль побочной оси), то они пересекаются в соответствующей точке А фокальной плоскости (рис. 12.16). Таким образом, фокальная плоскость есть плоскость, сопряженная бесконечно удаленной плоскости.

Рис. 12.16. Положение фокусов, расположенных на главной и побочной оптических осях тонкой линзы

( AF — фокальная плоскость линзы)

Для определения фокусных расстояний имеем следующие соотношения:

при а 1 = –∞