1.3. Понятие тесноты связи

Заметим, что сдвиг b нельзя считать объективной характеристикой зависимости Y от X, потому что его величина определяется выбором начала координат. Из соотношения (5), в частности, следует, что для МНК-оценок прямая, задаваемая уравнением (2), всегда проходит через точку ( ). Подставив (5) в (2), после несложных преобразований получим:

. (6)

Это соотношение связывает отклонения оценки отклика и фактора от их выборочных средних значений. Переход от величин к их отклонениям от сред­него называется центрированием этих величин. Заметим, что значение в соот­ношении (6) не присутствует.

На первый взгляд кажется, что по величине коэффициента можно су­дить о степени зависимости Y от X: чем больше , тем сильнее зависимость. Это не совсем так, потому что на величину влияет выбор единиц измерения X и Y. Для получения более объективной, чем , характеристики зависимости X и Y, следует найти связь между их нормированными значениями. Нормировку обычно проводят делением величины X (и, соответственно, Y) на ее выбороч­ное среднее квадратичное отклонение s_x (s_y). Разделим обе части соотноше­ния (6) на s_y, а затем правую часть умножим и разделим на s_x. Тогда получим:

(7)

где введено обозначение:

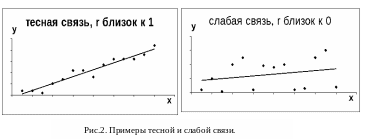
Величина r называется выборочным коэффициентом корреляции (см. Приложение). Коэффициент r показывает, на сколько значений s_y в среднем увеличится отклик, если фактор увеличится на s_x. Говорят, что выборочный коэффициент корреляции характеризует тесноту связи между X и Y.

Известно, что |r| ≤1. Чем ближе |r| к 1, тем теснее связь между X и Y; чем ближе |r| к 0, тем слабее связь. При r=1 точки наблюдений лежат на прямой, задаваемой соотношением (2). При r=0 прямая (2) параллельна оси абсцисс, и связь между X и Y отсутствует. Примеры тесной и слабой связи даны на рис.2.

1.4. Классическая нормальная линейная регрессионная модель

Рассмотрим вопрос о качестве МНК-оценок (4) и (5). Эти оценки обла­дают многими хорошими свойствами, если величины в уравнении (1) удовлетворяют следующим условиям.

• X – детерминированная величина;

• e₁, …,e_n – независимые нормальные одинаково распределенные случайные величины: e_i~N(0,s²), M(e_ie_j)=0 при ij.

При выполнении этих условий соотношение (1) называется классической нор­мальной линейной регрессионной моделью.

Справедлива теорема Гаусса-Маркова: В условиях классической нормальной линейной регрессионной модели^ оценки (4) и (5) имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Оценки, имеющие наименьшую дисперсию, называются эффективными. Таким образом, по теореме Гаусса-Маркова в условиях классической нормальной регрессионной модели МНК-оценки параметров парной линейной регрессии являются эффективными в классе всех линейных несмещенных оценок.

Упрощенная интерпретация теоремы Гаусса-Маркова: в среднем оценки (4) и (5) меньше, чем любые другие линейные несмещенные оценки, полученные по данным наблюдениям, отклоняются от истинных (но неизвестных) значений параметров m и b.

Кроме того, можно доказать (см., например, [5]), что в условиях классической нормальной регрессионной модели оценки (4) и (5) обладают следующими свойствами^:

1. – состоятельные оценки параметров m и b.

2. – несмещенные оценки параметров m и b ( ).

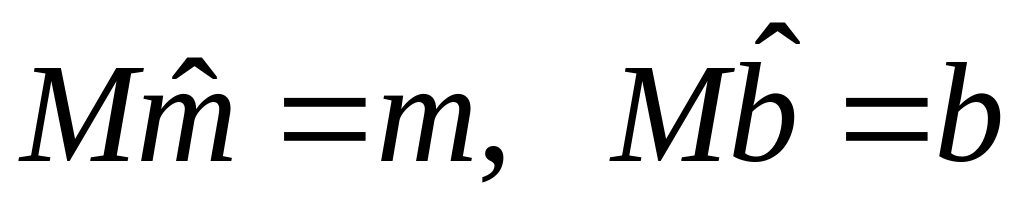3. Для дисперсии оценки справедлива формула:

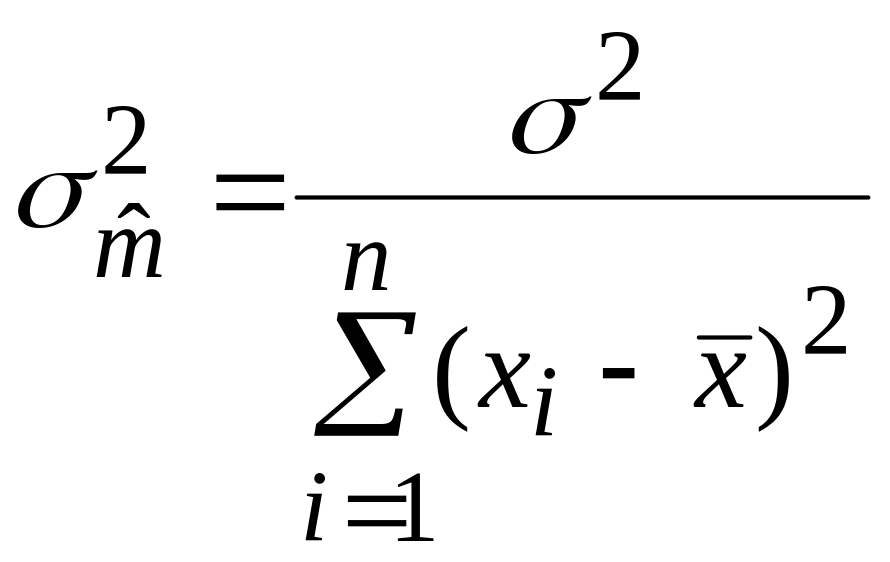(8)

4. являются нормальными случайными величинами.

5. Остаточная сумма квадратов Q_e независима от , а статистика

(8а)

имеет распределение хи-квадрат с числом степеней свободы n-2 (²_n-2).

6. Cтатистика s^2:

(8б)

является несмещенной оценкой дисперсии возмущений (Ms²=²).