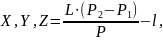2.4 Анализ точности текущего процесса измерения координат центра масс
2.4.1 Источники и закономерности погрешности метода
Точность в определении центра масс ведёт к возможности корректировки его координат (балансировке). Это особенно важно в авиационном приборостроении, где центр общий масс складывается из положения координат центра масс множества входящих приборов, устройств, изделий. В случае ремонта и замены большого количества приборов, если их центр масс будет существенно отличатся от ранее установленных изделий, то потребуется корректировка систем под новое положение центр масс. Поэтому так важно обеспечить качественную взаимозаменяемость приборов, а для этого требуется на предприятии изготовителе выполнять качественный контроль с минимальными потешностями.
Расчёт искомого результата осуществляется по формуле:
|
(2) |
где P – масса изделия (изделия и переходника если необходим);
P1 – масса действующая от силы тяжести стенда;
P2 – масса действующая от силы тяжести системы изделие с переходником и стенда;
L – Конструктивное расстояние между опорами, L=1000 мм;
l – Расстояние от базовой поверхности до первой опоры.
Как видно из формулы на точность измерения влияют погрешности измерения массы (погрешность весов) и базирования. Для устранения влияния погрешностей взвешивания на точность каждое измерение проводят три раза, а при расчёте используют среднее значение, что уменьшает производительность процесса.
Применяются весы ВТ-60 изготовленные по ГОСТ 29329-92. Наибольший предел взвешивания 60 кг. Дискретность отсчета 20 г. Наименьший предел взвешивания 400 г. Погрешность измерения ±10 г. Масса 18 кг.
Для измерения расстояний используется линейка 1000 ГОСТ 427-75. Погрешность измерения от ±0,05 до ±2 мм (±0,5 мм).
2.4.2 Расчёт погрешности
Произведём расчёт погрешности метода исходя из формулы (2).
Для каждой из координат абсолютная погрешность будет складывается из следующих неопределённостей:
(3)
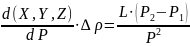
(4)
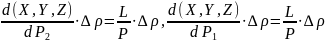
(5)
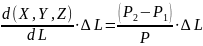
(6)
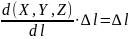
(7)
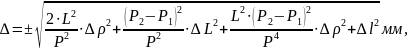
где ∆ – абсолютную погрешность определения выбранной координаты ЦМ;
∆L – абсолютная погрешность размера L, ∆L=0,5 мм;
∆l – абсолютная погрешность размера l, ∆l=0,5 мм;
P – масса изделия (изделия и переходника если необходим), кг;
P1 – масса действующая от силы тяжести стенда, кг;
P2 – масса действующая от силы тяжести системы изделие с переходником и стенда, кг;
∆ρ – абсолютная погрешность измерения массы для выбранного типа весов, кг, ∆ρ =0,02 кг.
Зная конструктивные размеры приспособления, погрешность измерения весов и требование к погрешности по ГОСТ 17265-80 (30% от массы) с помощью программы Mathcad возможно создать матрицу значений и просчитать все вожможные варианты абсалютной погрешности ∆ нахождения координат центра масс в зависимости от массы изделия P.
2.4.3 Матемаическое моделирование при многочисленных взвешиваниях.
В программе Mathcad зададим диапазоны возожных значений переменных.
В условиях наименьшего предела взвешивания применяемых весов 0,4 и наибольшего 50 кг, примем диапазон значений массы изделий от 1 до 50 кг.
Выразим диапазон значений массы действующей от силы тяжести системы изделие с переходником и стенда на весы из диапазона возможных значений координаты центра масс, исходя из максимальных габаритов устанавливаемых изделий от 10 до 900 мм.
(8)
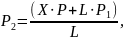
где X – диапазон возможных значений координаты.
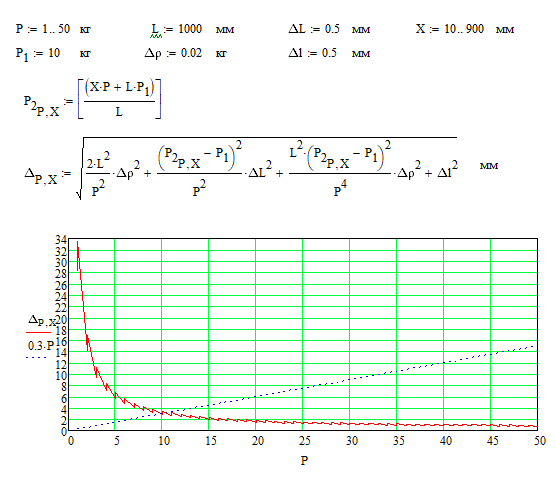
Рисунок 6 – Условия математического моделирования измерений, заданные в программе Mathcad
Множесво значения абсолюлютной погрешности измерений изделий массой от 1 до 50 кг, с координатой центра масс относительно первой опоры от 10 до 900 мм на весах c погрешность измерения ∆ρ кг изменяется согласно графикам.
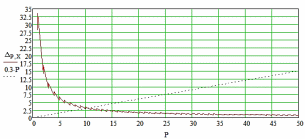
Рисунок 7 – График изменения абсолютной погрешности измерения ∆ в зависимости от массы контролируемого изделия P на весах с точностью ∆ρ = 0,02 кг.
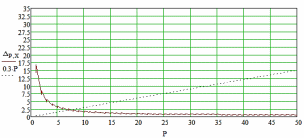
Рисунок 8 – График изменения абсолютной погрешности измерения ∆ в зависимости от массы контролируемого изделия P на весах с точностью ∆ρ = 0,01 кг.
По графику делаем вывод, что с помощью используемых весов с требуемой точностью возможно проконтролировать только изделия массой свыше 10 кг. Причём наблюдается обратная зависимость погрешности и назначаемых допусков ЦМ.
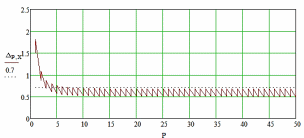
Рисунок 9 – График изменения абсолютной погрешности измерения ∆ в зависимости от массы контролируемого изделия P на весах с точностью ∆ρ = 0,001 кг при расположении координаты X в диапазоне от 10 до 900 мм.
Рисунок 10 – График изменения абсолютной погрешности измерения ∆ в зависимости от массы контролируемого изделия P на весах с точностью ∆ρ = 0,001 кг при расположении координаты X в диапазоне от 10 до 500 мм.
Как видно из графиков на рисунках 9 и 10 разброс значений абсолютной погрешности измерения ∆ зависит от расположения искомой координаты. Можно сделать вывод, что чем дальше расстояние до теоретического положения центра масс от левой опоры приспособления, тем больше разброс погрешности. При этом данное расстояние намного меньше влияет на точность, чем погрешность весов, особенно если находится в пределах 500 мм.
2.4.4 Экспериментальные исследования погрешности метода
Для практического примера и экспериментального анализа точности метода возьмём два изделия, лежащие на границах изготавливаемой номенклатуры продукции предприятием (крупногабаритное изделие сложной формы и маленький радиоэлектронный блок) и проведём сравнение измерений координат их центра масс.
Рисунок 11 – Изделия для исследования
Указанные в конструкторской документации (габаритный чертёж) координаты ЦМ изделия №1 – Х = 310±10 мм; Y = 425±15 мм; Z = 345±10 мм; при габаритных размерах 600х600х900 мм и изделия №2 – Х = 105±5 мм; Y = 220±10 мм; Z = 33±4 мм; при габаритных размерах 80х250х400 мм. Массами 45 и 2,2 кг.
Абсолютная погрешность используемого метода для изделий №1 и №2:
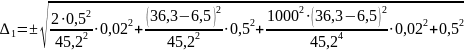
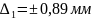
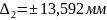
Таким образом на весах той же точности ∆ρ = 0,02 кг погрешность измерения превышает допустимые нормы и может выходить за пределы допуска на размер.
На габаритно-весовом макете, выполненном в программе SolidWorks, изображено графическое расположение центра масс изделий в 3D пространстве.
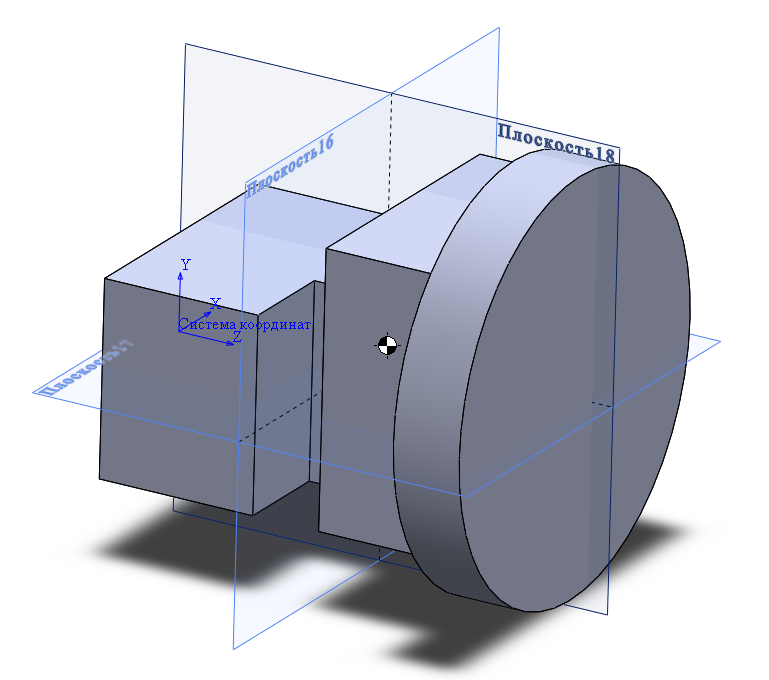
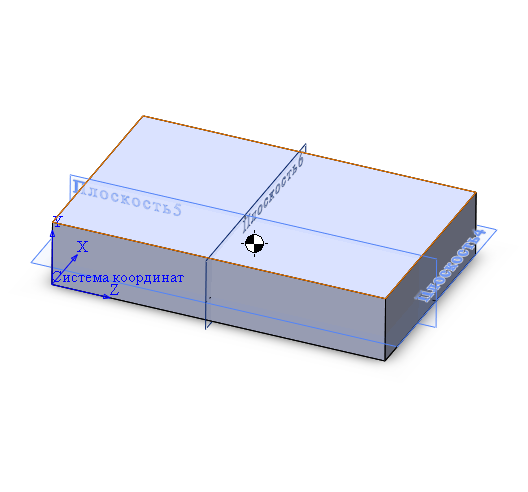
Рисунок 12 – Графическое расположение центра масс изделий в 3D
Таблица 2 – Данные замеров ЦМ партий изделий из 10 штук.
Деталь №1 |
Номер изделия из партии |
±∆ср, мм |
||||||||||
Размер, мм |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
310±10 |
310,3 |
309,0 |
310,7 |
311,5 |
310,7 |
309,4 |
308,4 |
310,5 |
310,2 |
308,6 |
0,431 |
|
±∆, мм |
0,180 |
0,442 |
0,371 |
0,787 |
0,405 |
0,272 |
0,778 |
0,279 |
0,132 |
0,663 |
||
425±15 |
424,0 |
425,8 |
426,1 |
425,1 |
423,2 |
424,0 |
426,3 |
423,5 |
425,3 |
425,9 |
0,502 |
|
±∆, мм |
0,470 |
0,456 |
0,578 |
0,099 |
0,849 |
0,462 |
0,673 |
0,727 |
0,190 |
0,515 |
||
345±10 |
346,1 |
343,5 |
345,2 |
344,1 |
346,4 |
346,4 |
345,8 |
344,5 |
344,2 |
346,4 |
0,483 |
|
±∆, мм |
0,411 |
0,887 |
0,022 |
0,568 |
0,555 |
0,597 |
0,284 |
0,383 |
0,552 |
0,566 |
||
Деталь №2 |
Номер изделия из партии |
|
||||||||||
Размер, мм |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
±∆ср, мм |
|
105±5 |
103,8 |
101,7 |
108,4 |
107,0 |
101,9 |
107,2 |
104,0 |
102,3 |
100,5 |
110,0 |
1,388 |
|
±∆, мм |
0,427 |
1,481 |
1,855 |
1,180 |
1,401 |
1,249 |
0,350 |
1,192 |
2,092 |
2,657 |
||
220±8 |
226,6 |
223,2 |
220,6 |
226,8 |
225,1 |
214,1 |
215,9 |
217,4 |
219,1 |
219,0 |
1,867 |
|
±∆, мм |
2,923 |
1,228 |
0,105 |
3,001 |
2,183 |
3,353 |
2,429 |
1,707 |
0,842 |
0,901 |
||
33±4 |
28,0 |
29,3 |
31,0 |
28,5 |
36,2 |
29,2 |
34,4 |
34,1 |
37,7 |
34,8 |
1,559 |
|
±∆, мм |
2,149 |
1,524 |
0,655 |
1,908 |
1,939 |
1,562 |
1,053 |
0,872 |
2,682 |
1,250 |
||
2.4.5 Выводы экспериментальные исследований погрешности метода
Таким образом в выборке из десяти значений трёх координат центра масс средняя величина абсолютной погрешности для изделия большей массы оказалась меньше и наоборот – изделие малой массы имеет погрешность при измерении близкую к допуску на размер. Что подтверждает прогноз математической модели.
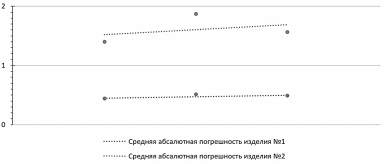
Рисунок 13 – Значения средней погрешности при измерении трёх координат
В результате проведённых исследований и экспериментов на имеющемся текущем оборудовании было выяснено, что используемый метод, как и оснастка для его осуществления нуждается в оптимизации. А именно, время, затрачиваемое на переустановку изделия, занимает слишком много времени и уменьшает производительность. При этом точность измерения напрямую зависит от погрешности применяемых весов, а ввиду того что метод основан на уравновешивании моментов, при уменьшении массы изделия ниже определённого порогового значения погрешность растёт в геометрической зависимости.
На основании конструктивных размеров, необходимой и действительной погрешности была построена область значений зависимости абсолютной погрешности от массы изделия и найден наименьший предел измерения используемого способа.