Вопрос 1.

Случайное событие. Вероятность.

2.

Случайная величина. Закон распределения.

Погрешность.

Классификация погрешностей измерений

Погрешность средств измерения и результатов измерения. В первую очередь погрешность измерений следует разделить на погрешность средств измерений и погрешность результатов измерений.

Погрешности средств измерений - отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).

Погрешность результата измерения - отклонение результата измерения от действительного (истинного) значения измеряемой величины , определяемая по формуле - погрешность измерения.

В свою очередь погрешности средств измерений можно разделить на инструментальную и методическую погрешности.

Инструментальные и методические погрешности. Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности. Статическая погрешность измерений - погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.

Динамическая погрешность измерений - погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. Более подробно соотношение между этими погрешностями рассмотрено в главе 4, где описаны виды регистрирующей аппаратуры.

Систематические и случайные погрешности. Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Случайными называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета. Случайные погрешности будут более подробно рассмотрены в следующем параграфе данной главы.

Погрешности адекватности и градуировки. Погрешность градуировки средства измерений - погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

В целом в теории планирования эксперимента погрешность адекватности может иметь большое значение, поскольку в многофакторных экспериментах чаще всего рассматривается линейная зависимость параметров состояния от факторов.

Абсолютная, относительная и приведенная погрешности. Под абсолютной погрешностью понимается алгебраическая разность между номинальным и действительным значениями измеряемой величины. - абсолютные погрешности (см.рис.2.1).

Однако в большей степени точность средства измерений характеризует относительная погрешность, т.е. выраженное в процентах отношение абсолютной погрешности к действительному значению измеряемой или воспроизводимой данным средством измерений величины. - относительные погрешности.

Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы. В этом случае пользуются понятием приведенной погрешности, равной отношению абсолютной погрешности измерительного прибора к некоторому нормирующему значению. В качестве нормирующего значения принимается значение, характерное для данного вида измерительного прибора. Это может быть, например, диапазон измерений, верхний предел измерений, длина шкалы и т.д. - приведенные погрешности, где и - диапазон изменения величин. Выбор и в каждом конкретном случае разный из-за нижнего предела (чувствительности) прибора.

 

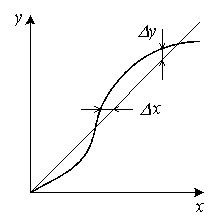
Рис. 2.1

Класс точности прибора — предел (нижний) приведенной погрешности.

Аддитивные и мультипликативные погрешности. Аддитивной погрешностью называется погрешность, постоянная в каждой точке шкалы.

Мультипликативной погрешностью называется погрешность, линейно возрастающая или убывающая с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (рис.2.2).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (рис.2.2, а). Иногда аддитивную погрешность называют погрешностью нуля.

 

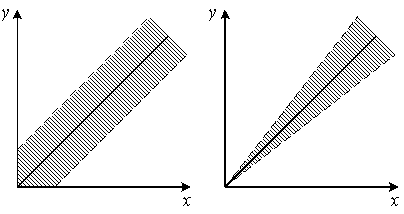
а б

Рис. 2.2

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (рис.2.2, б).

Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

- для аддитивной погрешности:

,

где - верхний предел шкалы, - абсолютная аддитивная погрешность.

- для мультипликативной погрешности

.

- это условие определяет порог чувствительности прибора (измерений).

Абсолютная величина погрешности для обоих типов погрешностей может быть выражена одной формулой:

, (2.1.1)

где - аддитивная погрешность, -мультипликативная погрешность.

Относительная погрешность с учетом (2.1.1) выражается формулой

,

и, при уменьшении измеряемой величины, возрастает до бесконечности. Приведенное значение погрешности

возрастает с увеличением измеряемой величины.

Нормирование погрешности средств измерений. Кроме нормирования погрешностей в виде класса точности возникает необходимость нормировать их некоторыми особыми способами. Например, нормирование погрешности цифрового частотомера или моста для измерения сопротивлений. Особенность этих приборов состоит в том, что кроме нижнего порога чувствительности мосты для измерения сопротивлений имеют верхний порог, а для цифрового частотомера погрешность зависит не только от измеряемой величины, но и от времени измерений.

Вопрос об измерении частот и временных интервалов будет рассмотрен ниже.

Нормировка при измерении сопротивлений имеет вид:

,

где — нижний и верхний пороги измеряемых сопротивлений.

Округление погрешностей обычно осуществляется до десятичного знака, соответствующего погрешности.

Вероятностная оценка случайной погрешности

Характеристики статистических распределений. Вероятность того, что случайная величина принимает значения в некотором интервале записывается в виде

, (2.2.1)

где называется плотностью распределения вероятности случайной величины . Для краткости функцию часто называют статистическим распределением. Поскольку находится в интервале с вероятностью равной единице, функция удовлетворяет условию нормировки

. (2.2.2)

С учетом статистического распределения случайной величины ее среднее значение вычисляется по следующей формуле:

. (2.2.3)

Если из генеральной совокупности всех возможных значений непрерывной случайной величины осуществляется конечная выборка дискретных значений , то элементарный расчет среднего значения по формуле

(2.2.4)

соответствует определению среднего (2.2.3) только при . Таким образом, даже для оценки точности вычисления средней величины необходимо учитывать форму статистического распределения исходных данных.

Статистические распределения принято оценивать по значениям их моментов. Моменты случайных величин, найденные без исключения систематических составляющих, называются начальными, а моменты для центрированных распределений — центральными.

Центральный момент -го порядка для непрерывной случайной величины рассчитывается по формуле

, (2.2.5)

при этом - математическое ожидание; - дисперсия (для конечной выборки — среднеквадратичное отклонение (СКО)); характеризует асимметрию распределения, а безразмерный коэффициент асимметрии есть третий центральный момент, поделенный на СКО; характеризует протяженность распределения, отношение - эксцесс, -характеризует остроту вершины распределения.

Наиболее широкое распространение при обработке экспериментальных данных получил центральный момент второго порядка который повсеместно используют для оценки погрешностей измерений. Для конечной выборки (конкретного числа отсчетов ) СКО принято рассчитывать по следующей формуле:

. (2.2.6)

Эта формула, как и формула (2.2.4) для вычисления , не учитывает форму распределения и не является строгой. Ее широкое использование обусловлено двумя основными причинами:

1.             Это наиболее простая возможность оценить рассеяние случайной величины.

2.             Значения случайных величин при экспериментальных измерениях имеют статистическое распределение, близкое к нормальному (гауссову), а для этого распределения среднеквадратичное отклонение и квадрат дисперсии совпадают.

Оценку асимметрии и эксцесса при конечной выборке осуществляют по следующим формулам

, (2.2.7)

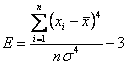. (2.2.8)

Число 3 в формуле (2.2.8) определяет эксцесс нормального распределения. Если эксцесс распределения отрицательный, то вершина функции распределения острее, чем у нормального распределения.

Определение этих характеристик распределений (моментов) называется точечными оценками, которые характеризуют распределение достаточно грубо.

Пусть в процессе экспериментальных измерений регистрируется сразу несколько случайных величин , каждая из которых имеет свое среднее значение и дисперсию . Многомерная случайная величина будет иметь многомерное распределение вероятностей с условием нормировки

.

Величины считаются статистически независимыми, если . Но эти величины могут быть статистически связаны, и для численной оценки этой связи двух случайных величин принято использовать смешанный момент второго порядка который называют корреляционным моментом или ковариацией.

Для расчета корреляционного момента используется следующая формула:

, (2.2.9)

где черта сверху означает статистическое усреднение соответствующего выражения. Корреляционный момент есть смешанная дисперсия двух величин, поэтому для расчета коэффициента корреляции используется нормировка на дисперсию каждой из случайных величин:

. (2.2.10)

Коэффициент корреляции меняется в пределах от -1 до +1 и определяет степень связи случайных величин.

Правила сложения случайных погрешностей. При сложении погрешностей в сложных измерительных системах необходимо учитывать, насколько эти погрешности статистически независимы или коррелированы. Из приведенных выше формул может быть получено следующее правило сложение погрешностей двух случайных величин:

, (2.2.11)

а дисперсия их суммы .

Таким образом, складывать СКО необходимо с учетом того, насколько случайные погрешности коррелированы.

Если:

1)    , то ;

2)    , то .

Как правило, при сложении погрешностей их делят на две группы: коррелированные и некоррелированные. Разделение на большее число групп (некоррелированные, слабо коррелированные, сильно коррелированные) слишком трудоемко. Поэтому на практике коррелированными погрешностями считаются те, у которых , остальные — некоррелированные.

Рассмотрим пример коррелированных погрешностей. Пусть измеряется зависимость активного сопротивления металлического проводника (длина , площадь сечения ) от температуры . Полученная экспериментально зависимость используется для проверки известной зависимости удельного сопротивления металлов от температуры

. (2.2.12)

Для вычисления по экспериментальным данным приходится использовать размеры проводника: . Но размеры проводника, также как и его удельное сопротивление, зависят от температуры по законам теплового расширения. На построение зависимости (2.2.12) будут влиять погрешности измерения , но погрешности в измерении при разных значениях температуры неизбежно будут связаны (коррелированы).

Центральная предельная теорема и распределение Гаусса. Как уже отмечалось, в подавляющем большинстве случаев считается, что случайные погрешности экспериментальных измерений имеют нормальное (гауссово) статистическое распределение. Этот факт имеет математическое обоснование в виде центральной предельной теоремы (ЦПТ – теорема):

Пусть случайная величина представляет собой сумму случайных величин , т.е. Если статистически независимы, то при их произвольном распределении и их сумма имеет нормальное распределение с плотностью вероятности

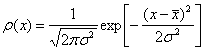. (2.2.13)

Зависимость имеет колоколообразную форму с вершиной в точке и полушириной .

Таким образом, широкое распространение нормального статистического распределения имеет глубокую физическую природу: если случайная величина зависит от большого числа случайных факторов, то она имеет нормальное распределение вне зависимости от характеристик каждого из этих факторов.

Построение функциональных зависимостей при многократных измерениях. Пусть необходимо построить зависимость в том случае, если каждому значению соответствует набор значений . В практических задачах в результате эксперимента имеется набор точек с координатами , как это показано на рис.2.3.

Наиболее очевидный и традиционный способ построения зависимости заключается в следующем: для каждого значения в определенном интервале находится среднее значение по попавшим в интервал точкам

и рассчитывается среднеквадратичное отклонение , где .

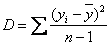При этом возникает необходимость в расчете погрешности определения , а значение СКО не дает возможности оценить достоверность оценки. Таким образом, возникают вопросы:

1)      с какой вероятностью значения попадают в обозначенный СКО интервал?

2)      насколько точна оценка ?

3) Как распределены значения в этом интервале?

Рис.2.3

 

В общем случае определение СКО не является лучшим способом оценки погрешностей. Чаще всего его используют на практике потому, что это единственная оценка, легко рассчитываемая в аналитическом виде.

Суть вероятностного описания полосы погрешностей искомой зависимости состоит в том, что необходимо сделать следующее утверждение: при данном значении принимает значение в определенном интервале (доверительном) с необходимой вероятностью (рис.2.3).

Основная проблема для такого заключения состоит в конечности выборки , где . Чаще всего в таких задачах используются квантильные оценки. Квантиль — прямая , делящая плотность вероятности на определенные части. На рис.2.4 показаны 50-, 25- и 5-процентные квантили для нормального распределения.

 

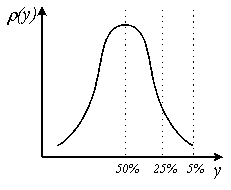
Рис.2.4

Грубая оценка интервала неопределенности и определение доверительного значения погрешности проводятся следующим образом: погрешности располагаются в порядке возрастания . Тогда в предположении равномерного распределения квантилей делят график плотности вероятности на часть. Отбросив крайние значения и , получим, что вероятность попадания величины в диапазон равна .

Таким образом, на основании изложенного можно утверждать, что оценка погрешности определена с доверительной вероятностью не более чем в доверительном интервале . Это самая грубая оценка.

Описанный способ предполагает равномерное распределения в заданном интервале, что на практике никогда не выполняется.

Часто кроме крайних значений величины отбрасывается определенное число . В этом случае

. (2.2.14)

 

Неравенство (2.2.14) предполагает, что для фиксированной доверительной вероятности можно определить необходимое количество отсчетов

. (2.2.15)

С увеличением выборки можно увеличить доверительную вероятность попадания в заданный интервал. В таблице 2.1 приведен необходимый объем выборки для заданных значений , рассчитанный по формуле (2.2.15) при .

 

Таблица 2.1

	0,8	0,9	0,95	0,98	0,99	0,995	0,997
	20	40	80	200	400	800	1333

 

Поскольку для значений требуется слишком большая выборка , то обычно для статистических оценок (в социально-экономических науках) используется .

СКО при вычислении среднего зависит от числа отсчетов как

, (2.2.16)

то есть при усреднении величины по отсчетам мы уменьшаем рассеяние данных в раз.

Чтобы перейти от оценки СКО к оценке доверительного интервала с учетом вероятности , необходимо учитывать статистическое распределение .

Закон распределения средней величины всегда близок к нормальному вне зависимости от того, как распределены исходные данные . Это следует из центральной предельной теоремы (ЦПТ) и справедливо при . Поэтому переход от оценки СКО к квантильной оценке доверительного интервала с доверительной вероятностью осуществляется следующим образом

, (2.2.17)

где - нормированная квантиль нормального распределения, соответствующая . Смысл определения величины заключается в том, что в зависимости от размеров выборки доверительный интервал может изменяться по отношению к оценке СКО. Доверительному интервалу всегда необходимо поставить в соответствие или уровень значимости . Значения , соответствующие разным уровням значимости для нормального распределения (выборка ) приведены в таблице 2.2.

Таблица 2.2

	0,8	0,9	0,95	0,98	0,99	0,995	0,998
	0,2	0,1	0,05	0,02	0,01	0,005	0,002
	1,28	1,64	1,96	2,33	2,58	2,81	3,09

 

Величина определяется следующим выражением:

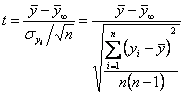, (2.2.18)

где - среднее значение для генеральной совокупности с нормальным распределением.

Статистическое распределение - известное распределение Стьюдента (рис.2.5).

Распределение Стьюдента. Его плотность вероятности описывается через специальные функции:

, (2.2.19)

где параметр определяется числом степеней свободы . Гамма-функция обладает следующими свойствами:

; ; .

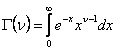На рис.2.5 приведено распределение Стъюдента при (кривая 2) и нормальное распределение (кривая 1). Как видно из рисунка, распределение Стъюдента симметрично и несколько шире нормального распределения, и совпадает с ним при . Основной смысл этого распределения состоит в том, что оно описывает отклонения среднего значения , рассчитанного по малой конечной выборке () от среднего значения генеральной совокупности .

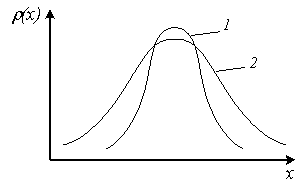
Рис.2.5

Это распределение широко табулировано и значение при вычислении доверительного интервала по формуле (2.2.17) для конкретной выборки всегда можно найти в справочной литературе. Величины для двух значений уровня значимости приведены в таблице 2.3.

Таблица 2.3

	2	3	4	5	7	10	15	20	30
	6,31	2,92	2,35	2,13	1,94	1,83	1,76	1,73	1,70	1,64
	12,7	4,30	3,18	2,78	2,45	2,26	2,14	2,09	2,04	1,96

 

Как видно из таблицы, при значения сильно возрастают и доверительный интервал в несколько раз превышает СКО (см. 2.2.17), что делает оценку практически бессмысленной. Однако при отличие квантили от ее значения для нормального распределения не превышает 30% . Распределение Стъюдента используется именно для такого объема выборки из генеральной совокупности, распределенной по нормальному закону.

Построение статистических распределений и критерии оценивания. Таким образом, для построения вероятностной модели эксперимента необходимо знать, по какому закону распределены экспериментальные данные. Для оценки закона распределения служат различные критерии, позволяющие с определенной вероятностью по конечной выборке оценить распределение генеральной совокупности данных.

В общем случае для оценки статистического распределения необходимо действовать по следующему алгоритму:

1.Построение гистограммы.

1.1.         Нахождение центра.

1.2.         Симметрирование гистограммы.

1.3.         Сглаживание.

2.Аппроксимация полученной гистограммы к распределению.

3.Проверка построенного распределения по критериям согласия.

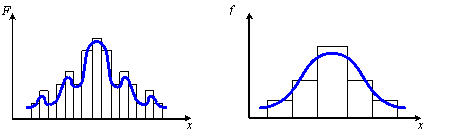
При построении гистограммы (рис.2.6) важно выбрать необходимое число интервалов в которые попадает случайная величина (обычно ). Затем по вертикальной оси гистограммы откладывается количество отсчетов или нормированная частота , попадающих в -й интервал (- общий объем случайной выборки). Если при малой выборке выбрано слишком большое число столбцов , то гистограмма может оказаться очень неравномерной (см. рис. 2.6,а) и судить о форме статистического распределения невозможно. Если исходить из того, что генеральная совокупность имеет гладкую форму распределения, то выбросы и провалы в гистограмме можно считать случайным шумом вызванным попаданием в тот или иной столбец. Тогда задачу выбора числа можно считать задачей оптимальной фильтрации. должно быть таким, чтобы максимально сглаживать но при этом минимально искажать случайную зависимость, описывающую распределение.

 

а б

Рис.2.6

Для выбора числа в литературе предлагается большое количество формул, мы приведем лишь три из них:

1)                       формула Старджеса: ;

2)                       ;

3)                       .

В предположении симметричности распределения число столбцов должно быть нечетным для однозначного определения центра распределения. Для его нахождения рассчитывают медиану или 50% - квантиль (половина выборки – больше, а половина – меньше этого числа). Медиана может не совпадать со средним значением .

Симметрирование гистограммы состоит в переносе некоторого числа отсчетов из данного столбца в симметричный с ним столбец для их выравнивания.

Построение сглаженной гистограммы и методы ее аппроксимации функциональной зависимостью будут рассмотрены в следующей главе.

Для идентификации распределения используются критерии согласия. Наиболее распространен критерий (критерий Пирсона). Он используется при проверке гипотез о принадлежности выборки к определенной генеральной совокупности.

Для этого выбирается по формуле

,

где - число значений случайной величины, попавшей в -й интервал (высота столбца в гистограмме на рис.2.7); - значение частоты в выбранной модели распределения.

 

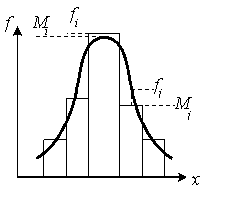
Рис.2.7

Критерий Пирсона дает , если в центрах всех столбцов гистограммы выполняется равенство .

Критерий , кроме того, позволяет произвести сравнение двух моделей распределений в том случае, если для них используется разное число столбцов.

В общем случае существенно возрастает с увеличением числа столбцов, но для квантилей распределения имеются специальные таблицы, в которых используется число степеней свободы

,

где - число параметров, необходимых для описания распределения.

Для нормального распределения достаточно определить первые два момента, поэтому . В отличие от распределения Стьюдента, рассчитанного для нормальной генеральной совокупности, критерий может использоваться для любых распределений.

Второй пример широко используемого критерия - критерий Колмогорова-Смирнова. Он позволяет сравнить две независимые выборки и ответить на вопрос, относятся ли они к одной генеральной совокупности. Его удобство состоит в том, что для использования нет необходимости строить гистограмму.

В качестве статистики служит наибольшая по модулю разница между нормированными частотами в двух выборках

.

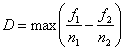При (рис.2.8) .

Величина табулирована и для можно задать граничное значение

,

где - постоянная, зависящая от уровня значимости (вероятность ошибки при идентификации распределения). Для этой величины имеется приближенная аналитическая формула . Если выборка объемом сопоставляется с аналитической моделью распределения (), то . Отсюда может быть оценена вероятность ошибки идентификации распределения по выборке объемом :

.

 

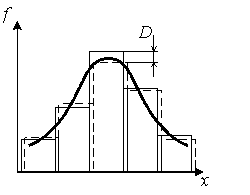
Рис.2.8

Для оценки разницы между дисперсиями двух конечных выборок из нормальной совокупности используется критерий Фишера. В качестве значения критерия берут отношение большей дисперсии к меньшей

,

где — среднеквадратичные отклонения.

Вычисленное таким образом значение критерия сравнивается с табулированным значением в соответствии с уровнем значимости для степеней свободы и распределений ( и — величины выборок).

 

 

Обработка результатов прямых измерений. Пусть результаты  прямых измерений равны . Предположим, что истинное значение измеряемой величины равно , тогда - погрешность -го измерения.

Относительно погрешности предполагаются следующие допущения:

1) - случайная величина с нормальным распределением.

2) Математическое ожидание  (отсутствует систематическая погрешность).

3) Погрешность  имеет дисперсию , которая не меняется в зависимости от номера измерения, т.е. измерение равноточное.

4) Измерения независимы.

При этих допущениях плотность распределения результата измерения  запишется в виде:

.                         (2.3.1)

В данном случае истинное значение измеряемой величины  входит в формулу (2.3.1) как параметр.

Вследствие независимости отдельных измерений плотность распределения системы величин  выражается формулой:

.                              (2.3.2)

С учетом (2.3.1) и независимости  их многомерная  плотность распределения (2.3.2) представляет собой функцию правдоподобия:

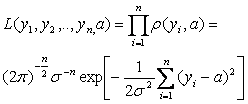.                   (2.3.3)

Используя функцию правдоподобия (2.3.3) необходимо найти оценку  для измеряемой величины  таким образом, чтобы в (2.3.3) выполнялось условие:

.                                       (2.3.4)

Для выполнения (2.3.4) необходимо, чтобы

.                                               (2.3.5)

По-сути условие (2.3.5) является формулировкой критерия наименьших квадратов, т.е. для нормального распределения оценки по методу наименьших квадратов и методу максимального правдоподобия совпадают.

Из (2.3.4) и (2.3.5)  можно получить также наилучшую оценку

.                                                     (2.3.6)

Важно понимать, что полученная оценка  является случайной величиной с нормальным распределением. При этом 

.                                            (2.3.7)

Таким образом, получая , мы увеличиваем точность измерений, т.к. дисперсия этой величины в n раз меньше дисперсии отдельных измерений. Случайная погрешность при этом уменьшится в  раз.

Для оценки неопределенности величины  необходимо получить оценку погрешности (дисперсии). Для этого прологарифмируем функцию максимального правдоподобия (2.3.3) и оценку дисперсии найдем из условия  

.                      (2.3.8)

После дифференцирования получим

,                           (2.3.9)

а далее, из (2.3.9)  - оценку дисперсии :

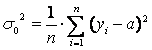.                                             (2.3.10)

Таким образом мы доказали, что для нормально распределенных данных СКО является лучшей оценкой дисперсии.

 Обработка результатов косвенных измерений. Пусть при косвенных измерениях величина  рассчитывается по экспериментальным данным, полученным по  измерениям величин :

.                                         (2.3.11)

Запишем полный дифференциал функции:

.  (2.3.12)

 

В случае слабой зависимости функции от аргументов её приращение может быть выражено в виде линейной комбинации . Согласно (2.3.12) получим:

.                                                          (2.3.13)

Каждое слагаемое в (2.3.13) представляет собой частную погрешность результата косвенных измерений.

Производные  называется коэффициентами влияния соответствующих погрешностей.

Формула (2.3.13) является приближённой, т.к. учитывает только линейную часть приращений функции.  В большинстве практических случаев такое приближение оправдано.

   Если известны систематические погрешности  прямых измерений  , то формула (2.3.13) позволяет рассчитать систематическую погрешность косвенных измерений.  

Если частные производные в (2.3.13) имеют разные знаки, то происходит частичная  компенсация систематических погрешностей.

   Если формула (2.3.13) используется для вычисления предельной погрешности, то она принимает вид:

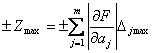.                                            (2.3.14)

Рассмотрим, как, используя формулу (2.3.13),  можно оценить случайную погрешность косвенных измерений.

Пусть погрешность прямых измерений  имеет нулевое математическое ожидание  и дисперсию .

   Использую (2.3.13) запишем выражения для математического ожидания и дисперсии  погрешности косвенных измерений . Математические ожидания отдельных измерений складываются с учетом вклада каждого из них:

.                                       (2.3.15)

Для вычисления дисперсии воспользуемся правилом сложения погрешностей:

,        (2.3.16)

где -коэффициент корреляции погрешностей . Если  погрешности  не коррелированны, то

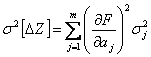.                                            (2.3.17)

 

 Обработка результатов совместных измерений. При совместных измерениях полученные значения используются для построения зависимостей между измеряемыми величинами. Рассмотрим многофакторный эксперимент, по результатом которого должна быть построена зависимость . Предположим далее, что зависимость  , то есть параметр состояния есть линейная комбинация из входных факторов. В процессе эксперимента проводится  совместных измерений для нахождения коэффициентов .

   В этом случае искомые величины определяются в результате решения системы линейных уравнений:

,                                 (2.3.18)

где  - искомые коэффициенты зависимости, которую необходимо определить, - измеряемые значения величин.

   В предположении, что система уравнений (2.3.18) является точной, но значения  получены с погрешностями, запишем:

,                                                                 (2.3.19)

где  - погрешность измерения  , тогда

.                                                        (2.3.20)

   Для решения задачи мы вынуждены использовать значения . При этом, если число измерений  больше числа неизвестных в уравнении (2.3.18) , то система (2.3.18) не имеет однозначных решений. Поэтому уравнения системы (2.3.18) иногда называют условными.

   Оценим случайную погрешность совместных измерений. Пусть погрешность  имеет нормальный закон распределения с нулевым математическим ожиданием и дисперсией. Измерения  независимы. В этом случае по аналогии с обработкой прямых измерений может быть построена функция максимального правдоподобия:

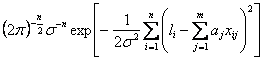.          (2.3.21)

   Для нахождения экстремума функции правдоподобия (2.3.21) воспользуемся уже известной процедурой. Прологарифмируем  (2.3.21) и найдём значения, при  которых функция достигает экстремума. Условие максимума функции (2.3.21) является:

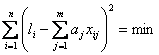.                                           (2.3.22)

   Таким образом ((2.3.22)) отвечает требованиям метода наименьших квадратов. Следовательно, при нормальном распределении случайной погрешности оценки по методу максимального правдоподобия и по методу наименьших квадратов совпадает.

   Для нахождения оценки  удовлетворяющей (2.3.22) необходимо добиться равенства нулю всех частных производных этой функции по  . Для каждого значения  эта оценка будет находиться из следующего уравнения:

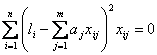.                                           (2.3.23)

Система уравнений (2.3.23) является линейной относительно  и называется системой нормальных уравнений. Число уравнений в системе всегда совпадает с числом .

Система (2.3.23) решается методом определителей

,

где - определитель матрицы , а определитель   получается из определителя  заменой -го столбца столбцом свободных членов.

Для нахождения оценки дисперсии результатов  найдем условие максимума после логарифмирования (2.3.21)  и подставим (см. (2.3.8-2.3.10)), получим

.

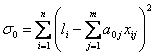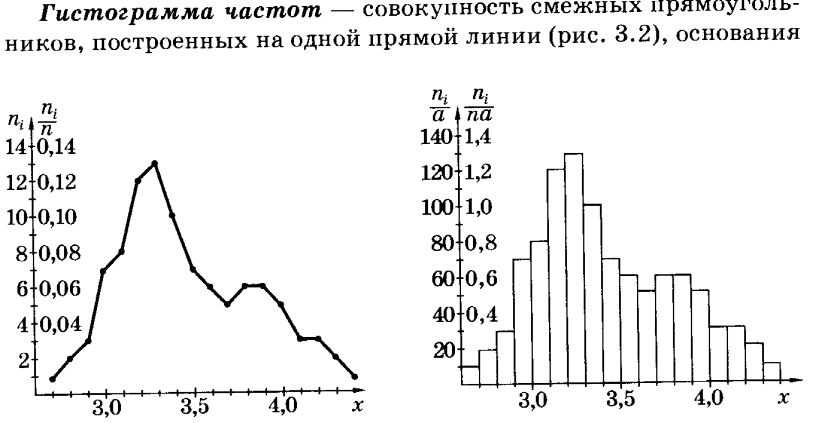
3. Нормальный закон распределения.

Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Плотность вероятности

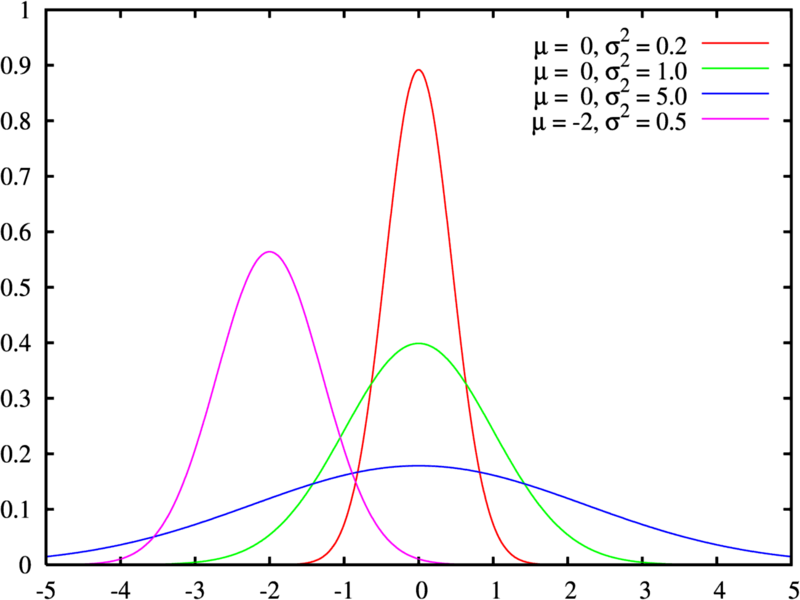
Зеленая линия соответствует стандартному нормальному распределению

Кривая распределения нормального закона(Кривая Гаусса)

1°. Областью определения функции f(x) является вся числовая ось.

2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.

3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.

4°. Функция f{x) имеет в точке х = a максимум, равный

5°. График функции f(x) симметричен относительно прямой х = а.

6°. Нормальная кривая в точках х = а +s имеет перегиб,

На основании доказанных свойств построим график плотности нормального распределения f(x).

Среднеквадратическое отклонение

Среднеквадрати́ческое отклоне́ние — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.

Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднеквадратическое отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

Среднеквадратическое отклонение:

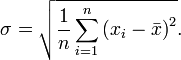
Доверительный интервал

Рассмотрим использование t-критерия Стьюдента для построения доверительного интервала для математического ожидания.

При t=tкр разность [X - M{Х}] в (1.3) равна половине ширины доверительного интервала __ т.е.

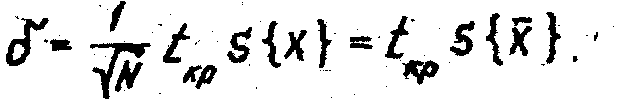
Доверительный интервал, в котором с доверительной вероятностью P=I-q находится математическое ожидание M{X} , определяется следующими выражениями:

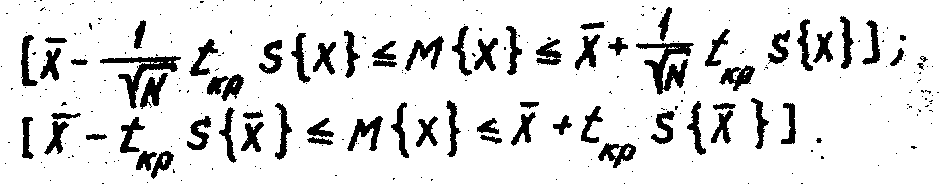
Поскольку математическое ожидание М{X} есть истинное, объективно существующее неслучайное значение, а границы интервала - случайные величины (за счет наличия в них случайных величин X и S{X}), то правильно будет говорить о том, что доверительный интервал (1.5), (1.6) с ве­роятностью Р = I - q накрывает М {X}.

Надежность

Надёжность объекта характеризуется следующими основными состояниями и событиями.

Исправность – состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической документацией (НТД).

Работоспособность – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров, установленных НТД.

Основные параметры характеризуют функционирование объекта при выполнении поставленных задач.

Понятие исправность шире, чем понятие работоспособность. Работоспособный объект обязан удовлетворять лишь тем требования НТД, выполнение которых обеспечивает нормальное применение объекта по назначению. Таким образом, если объект неработоспособен, то это свидетельствует о его неисправности. С другой стороны, если объект неисправен, то это не означает, что он неработоспособен.

Предельное состояние – состояние объекта, при котором его применение по назначению недопустимо или нецелесообразно.

Применение (использование) объекта по назначению прекращается в следующих случаях:

· при неустранимом нарушении безопасности;

· при неустранимом отклонении величин заданных параметров;

· при недопустимом увеличении эксплуатационных расходов.

Для некоторых объектов предельное состояние является последним в его функционировании, т.е. объект снимается с эксплуатации, для других – определенной фазой в эксплуатационном графике, требующей проведения ремонтно-восстановительных работ.

В связи с этим, объекты могут быть:

· невосстанавливаемые, для которых работоспособность в случае возникновения отказа, не подлежит восстановлению;

· восстанавливаемые, работоспособность которых может быть восстановлена, в том числе и путем замены.

В ряде случаев один и тот же объект в зависимости от особенностей, этапов эксплуатации или назначения может считаться восстанавливаемым или невосстанавливаемым.

Отказ – событие, заключающееся в нарушении работоспособного состояния объекта.

Критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт возникновения отказа.

Числовые характеристики случайной величины: математическое ожидание и дисперсия

Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение называется величина , если число значений случайной величины конечно.

Если число значений случайной величины счетно, то При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей px (x) вычисляется по формуле 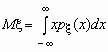При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x , h = f(x), то 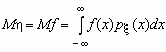Аналогичные формулы справедливы для функций дискретной случайной величины:

Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.

Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам ,

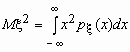
Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение , связанное с дисперсией соотношением

4. Распределение Стьюдента и его применение

Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма Сили Госсета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент».

Пусть — независимые стандартные нормальные случайные величины, такие что Тогда распределение случайной величины , где называется распределением Стьюдента с степенями свободы. Пишут . Её распределение абсолютно непрерывно и имеет плотность 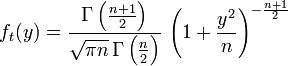где — гамма-функция Эйлера.

Функция распределения

Применение распределения Стьюдента

Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения. В частности, пусть независимые случайные величины, такие что . Обозначим выборочное среднее этой выборки, а её выборочную дисперсию. Тогда

Классы точности приборов

классом точности прибора, связанным с его устройством – элементной базой и принципом действия.

Абсолютная погрешность через класс точности оценивается следующим образом:

(Dx) к.т.= (g/100)A,

где g - класс точности в %, указанный на панели прибора,

А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;