
- •5. Формулы Муавра и Эйлера.
- •13. Замечательные пределы.
- •24. Использование понятия производной функции при описании характеристик экономических процессов.
- •29. Исследование функции спроса на товар, имеющих цену х.
- •36. Первообразная и неопределённый интеграл
- •42. Определенный интеграл как предел интегральной суммы в упрощенных задачах экономики.
- •48. Определение дифференциального уравнения. Порядок дифференциального уравнения.
- •50. Дифференциальные уравнения с разделяющимися переменными. Интегральные кривые.
- •56. Системы линейных дифференциальных уравнений. Методы решения.
- •57. Конечные и бесконечные числовые последовательности и ряды.
- •60. Знакопеременные ряды. Признаки сходимости.
1. Понятие множества. Множества конечные и бесконечные. Множество – это первоначальное понятие и не имеет строгого понятия; множество – это совокупность элементов. Множество можно создавать перечислением элементов. Элементы множества – отдельные объекты, из которых состоит множество. Конечное множество состоит из конечного числа элементов. Бесконечное множество состоит из бесконечного числа элементов, т.е. это мн-во, которое не является ни конечным, ни пустым. Пр.: множество действительных чисел, множество точек плоскости.
2. Подмножества.
Операции над множествами. Подмножество
– эта часть множества. Множество
А является подмножеством
множества
В, если любое х принадлежащее множеству
А, принадлежит множеству
В. Пересечение
множеств.
Пересечением множеств
А и В называется
множество С, состоящее из элементов,
одновременно входящих в оба множества.
Разность
. Разность
двух множеств А и В наз-ся множество С,
состоящее из элементов множества А, не
входящие в множество В
Объединение.
Объединением двух множеств
А и В называется
множество С, состоящее из элементов
множества А и множества В.
Симметрическая
разность.
Симметрической
разностью
множеств A
и B
наз-ся множество С, состоящее из всех
элементов обоих множеств, которые не
являются общими множеств А иВ.
3.
Системы координат на прямой, плоскости
и в пространстве.
Система
координат — комплекс определений,
реализующий метод координат, то есть
способ определять положение точки или
тела с помощью чисел или других символов.
Совокупность чисел, определяющих
положение конкретной точки, называется
координатами этой точки. В зависимости
от направления координатных осей
различают правую и левую прямоугольные
системы координат в трехмерном
пространстве.
4.
Комплексные
числа. Формы записи комплексных чисел.
Комплексным
числом Z наз-ся выражение вида Z=а+¡b, где
а и b- действительные числа, ¡-мнимая
единица.
алгебраическая форма записи Z=а+¡b
геометрические формы записи
: тригонометрическая
форма записи:z
= r(cos φ
+ isin φ).показательная
форма записи:z
= | z
| eiφ,где
![]() —
одно из значенийаргумента
комплексного числа (которое определяется
с точностью до 2π); он же — главный
аргумент
комплексного числа z:
—
одно из значенийаргумента
комплексного числа (которое определяется
с точностью до 2π); он же — главный
аргумент
комплексного числа z:
![]() а eiφ
— это продолжение экспоненциальной
функции на область комплексных чисел.
а eiφ
— это продолжение экспоненциальной
функции на область комплексных чисел.
5. Формулы Муавра и Эйлера.
Формула Муавра
![]()
![]() Формула Муавра сразу следует
из формулы Эйлера
Формула Муавра сразу следует
из формулы Эйлера![]() и
тождества для экспонент
и
тождества для экспонент![]() ,
где b — целое число Формула Эйлера
,
где b — целое число Формула Эйлера![]()
Доказательство
формулы Эйлера можно провести с
использованием рядов Тейлора. Разложим
функцию
![]() в
ряд Тейлора по степеням
в
ряд Тейлора по степеням![]() .6.
Отображения
и функции. Обратная функция.
.
Функция
(отображение, преобразование) —
математическое понятие, отражающее
связь между элементами множеств. Можно
сказать, что функция — это «закон», по
которому каждому элементу одного
множества (называемому областью
определения) ставится в соответствие
некоторый элемент другого множества
(называемого областью значений).
Обра́тная фу́нкция — функция, обращающая
зависимость, выражаемую данной функцией.
Ф-я g:
YX
является обратной к функции f
:XYесли
выполнены следующие тождества:1.f(g(y))=y
для всех y
принадлY
2. g(f(x))=x
для всех x принадлX.
Чтобы найти обратную функцию, нужно
решить уравнение x=F(y)
относительно y.
Если оно имеет более чем один корень,
то функции обратной к F не существует.
.6.
Отображения
и функции. Обратная функция.
.
Функция
(отображение, преобразование) —
математическое понятие, отражающее
связь между элементами множеств. Можно
сказать, что функция — это «закон», по
которому каждому элементу одного
множества (называемому областью
определения) ставится в соответствие
некоторый элемент другого множества
(называемого областью значений).
Обра́тная фу́нкция — функция, обращающая
зависимость, выражаемую данной функцией.
Ф-я g:
YX
является обратной к функции f
:XYесли
выполнены следующие тождества:1.f(g(y))=y
для всех y
принадлY
2. g(f(x))=x
для всех x принадлX.
Чтобы найти обратную функцию, нужно
решить уравнение x=F(y)
относительно y.
Если оно имеет более чем один корень,
то функции обратной к F не существует.
7. Экономические
зависимости и функции.
Функции находят
широкое применение в экономической
теории и практике. Спектр используемых
функций весьма широк: от простейших
линейных до функций, получаемых по
определенному алгоритму с помощью
рекуррентных соотношений, связывающих
состояния изучаемых объектов в разные
периоды времени. Наиболее часто
используются в экономике следующие
функции:1. Функция полезности (функция
предпочтения)- зависимость результата,
эффекта некоторого действия от уровня
(интенсивности) этого действия. 2.
Производственная функция- зависимость
результата производственной деятельности
от обусловивших его факторов. 3. Функция
выпуска- зависимость объема производства
от наличия или потребления ресурсов.
4. Функция издержек- зависимость издержек
производства от объема продукции. 5.
Функция спроса, потребления и предложения-
зависимость объема спроса, потребления
или предложения отдельные товары или
услуги от различных факторов( например,
цены, дохода и т.п.).
8.
Функции одной переменной.
Если
задано правило по которому каждому
значению перем. Величины х из мн-ва Х
ставится соответствие 1 значению перем.
У то в этом случае говорят, что задана
ф-ция 1-й переменной.
Y=f(x);
x
–аргумент независ. перемен., y-
зав. пер. X=Df=D(f)
y={y;y=f(x),xX}
x1X1,
y1=f(x1)
1) аналит. способ; 2)Табличный
способ;тт3) Графический способ; 4)Min
и max
ф-ции: ф-ция f(x)
ограничена, если огран. ее мн-во знач
У, т.е.
m,M:
mf(x)M
xXmf(x)
xX
=> огр. сн.; f(x)M,
xX=>
огр. св.
9.
Предел функции.Опр.
Точка х0
= а
![]() Е
называется точкой сгущения множества
А
Е
называется точкой сгущения множества
А![]() Е,
если произвольная окрестность точки
х0 содержит хотя бы одну точку множества
А, отличную отх0.
Сама точка х0
может принадлежать множеству А или не
принадлежать.
Предел
limx→x0-0
f(x)=C'
называется пределом функции f(x)
при x,
стремящимся к x0
слева, а предел limx→x0-0
f(x)=C''
– пределом функции f(x)
при x,
стремящимся к x0
справа.
Пусть
числовые функции f
(x)
и g
(x)
определены на некотором интервале,
быть может, кроме точки х0
этого интервала, и имеют конечные
пределы в этой точке
Е,
если произвольная окрестность точки
х0 содержит хотя бы одну точку множества
А, отличную отх0.
Сама точка х0
может принадлежать множеству А или не
принадлежать.
Предел
limx→x0-0
f(x)=C'
называется пределом функции f(x)
при x,
стремящимся к x0
слева, а предел limx→x0-0
f(x)=C''
– пределом функции f(x)
при x,
стремящимся к x0
справа.
Пусть
числовые функции f
(x)
и g
(x)
определены на некотором интервале,
быть может, кроме точки х0
этого интервала, и имеют конечные
пределы в этой точке
![]() и
и
![]()
Тогда
если | A | < ∞, то функция f (x) ограничена в окрестности точки х0.
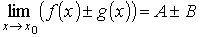
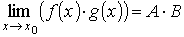
если
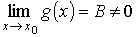 ,
то
,
то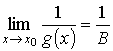 .
. и
и
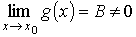 ,
то
,
то
 ,
то
,
то

Пусть в некоторой выколотой δ – окрестности точки х0 функции f (x) и g (x) определены и выполнено неравенство f (x) < g (x). Пусть существуют пределы
![]() и
и
![]() тогда
справедливо неравенство А ≤ B.
тогда
справедливо неравенство А ≤ B.
10. Элементарные функции. Элементарные функции — функции, которые можно получить из основных элементарных функций:
Степенная: y=x^n
Логарифмическая: y=log˅a x
Показательная: y=a^x
Тригонометрические: y=sin x
Обратные тригонометрические: y=arcsin x
11.
Операции над функциями, имеющими предел.
Точка
х0
= а
![]() Е
называется точкой сгущения множества
А
Е
называется точкой сгущения множества
А![]() Е,
если произвольная окрестность точки
х0 содержит хотя бы одну точку множества
А, отличную отх0.
Сама точка х0
может принадлежать множеству А или не
принадлежать.
Е,
если произвольная окрестность точки
х0 содержит хотя бы одну точку множества
А, отличную отх0.
Сама точка х0
может принадлежать множеству А или не
принадлежать.
![]()
![]() ,
в частности lim
C
f(x)=Climf(x)=CA,
где С- пост.величина
,
в частности lim
C
f(x)=Climf(x)=CA,
где С- пост.величина
![]() ,
где В ≠0
,
где В ≠0
ТЕОРЕМА1 Пусть функции f(x) и g(х) имеют в точке а пределы А и В. Тогда функции f(x) ± g{x), f(x)g(x) и f(x)/g(x) (при В ≠ 0) имеют в точке а пределы, равные соответственно А± В, А В и А/В.
ТЕОРЕМА 2. Пусть функции f(x), g(x) и h(x) определены в некоторой окрестности точки а за исключением, быть может, самой точки а, и функции f(x) и g(х), имеют в этой точке предел, равный А: lim f(x)= lim g(x)= A.Кроме того, пусть выполнены неравенства f(x) ≤ h(x) ≤ g(x). Тогда lim h(x)=A (*где предел, дописать ха) 3. Два замечательных предела 1)предел функции sinx/x в точке х =0 существует и равен единице 2) Предел функции f(x) = (1+1/x)в степ. Х при х∞ существует и равен е.
12.
Непрерывность и разрывы функций.
Непрерывная
функция — функция без «скачков», то
есть такая, у которой сколь угодно малые
изменения аргумента приводят к сколь
угодно малым изменениям значения
функции. Функция f(x) называется непрерывной
в точке x0,
если предел слева равен пределу справа
и совпадает со значением функции в
точке x0 , то есть![]() .ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ
НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ
ФУНКЦИИ В ЭТИХ ТОЧКАХ. Функция непрерывна
на множестве , если она непрерывна в
каждой точке данного множества. Если
оба односторонних предела существуют
и конечны, но хотя бы один из них отличен
от значения функции в данной точке, то
такую точку называют точкой разрыва
первого рода; если хотя бы один из
односторонних пределов не существует
или не является конечной величиной, то
такую точку называют точкой разрыва
второго рода.
.ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ
НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ
ФУНКЦИИ В ЭТИХ ТОЧКАХ. Функция непрерывна
на множестве , если она непрерывна в
каждой точке данного множества. Если
оба односторонних предела существуют
и конечны, но хотя бы один из них отличен
от значения функции в данной точке, то
такую точку называют точкой разрыва
первого рода; если хотя бы один из
односторонних пределов не существует
или не является конечной величиной, то
такую точку называют точкой разрыва
второго рода.
