181. Доведення додаткових теорем, що використовувалися при розкритті невизначеності .

Теорема 1. Послідовність притоді і тільки тоді, коли існує.

Доведення

а) Нехай Зафіксуємо довільне. За означенням границі, що.

Покладемо й оцінимо. Маємо, враховуючи монотонність функції,

.

Таким чином, , тобто.

Якщо всі , то.

Нехай послідовність складається зі всіх. Тоді з попереднього ()

.

Таким чином, .

б) Навпаки, нехай . Покажемо, що. Припустимо супротивне. Тодітака, що, тобто або, абодля всіх.

У першому випадку маємо

, а у другому . Отримали суперечність. Теорему доведено.

Теорема 2. Нехай , і для всіх. Тоді.

Доведення

Маємо .

За теоремою 1 , тобто.

Другий спосіб доведення пункту б.

б) Нехай . Покажемо, що. За означенням границі,, такий що приабо. Оскількимале, то.

Прологарифмуємо подвійну нерівність:

.

Позначимо за . Тоді. Таким чином, для, звідси випливає, що.

Теорема 3. , тоді.

Доведення. За теоремою 2 . Визначимо

182. Загальний випадок заміни змінної в подвійному інтегралі

Нехай Dвідкрита множина на площині ,G – відкрита множина на площині ,F–відображення Gна D і точки ,,. Відображеннязадається парою функцій,.

Припустимо, що задовольняє такі вимоги:

1. воно взаємно однозначно відображає Gна D, тобто ;

2. - неперервно диференційована на G;

3. якобіан

.

Нехай - відкриті множини, вимірювані,і такі, що при відображеннімножинавідображується на. Тодіі- обмежені замкнені множини, внутрішні точкипереходять у внутрішні точки, а границявідображується на границю.

Теорема. Нехай функція визначена і неперервна на. Тоді

Доведення. Зауважимо, що обидва інтеграли існують як інтеграли від неперервних функцій на замиканні вимірюваних областей.

Припустимо, що відображення F лінійне, тобто ,, деі якобіантоді

, .

Прямі ііз площиниUOV відображаються в прямі і, що лежать у площині ХОУ.

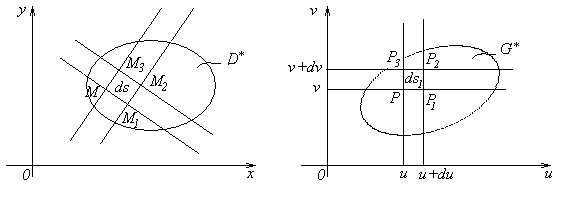Площа нескінченно малого елемента в площині UOV , а площа його відображення в площинуХОУ .

Координати точок

;

;

.

Координати векторів

, .

Площа відображення

.

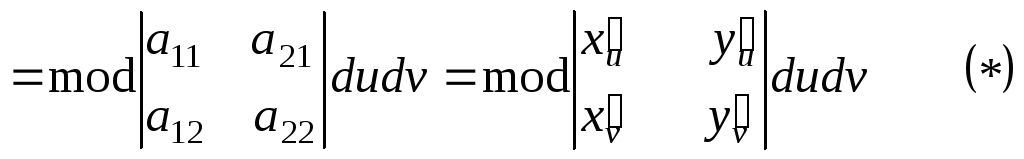Якщо ж відображення не є лінійним, тобто ,, і дані функції є неперервно диференційованими в областіG, то за формулою Тейлора

або

.

Аналогічно .

Можна довести, що в нелінійному відображенні площі нескінченно малих елементів іпов’язані знову-таки формулою (*) (у правій частині якої є доданок н.м. відносно).

Зауважимо, що «основа всього аналізу – це розгляд нелінійного функціонального відношення як лінійне в нескінченно малому» (Бурдак Б.М., Фомін С.В. «Кратные интегралы и ряды»).

183. Означення суми ряду .

У прикладі пункту 164 доведено, що при. Дослідимо отриманий ряд прих=1:

(1).

Оскільки ряд знакозмінний, то, використовуючи ознаку Лейбніца (п.152), перевіримо дві умови:

а) ;

б) , тобто послідовністьмонотонно спадає.

Оскільки всі умови ознаки Лейбніца виконуються, то ряд (1) збігається.

Ряд гармонічний. У п.150 доведено, що він розбіжний. Таким чином, ряд (1) умовно збігається.

За теоремою Абеля, якщо степеневий ряд збігається при x=R (R – радіус збіжності), то його сума зберігає неперервність (зліва) і при цьому значенні. Тобто

.

184. Ще одна достатня умова розвинення функції в ряд Тейлора

Теорема. Для того щоб функцію можна було розвинути в ряд Тейлора на інтервалідостатньо, щобf(x) мала на похідні всіх порядків і щоб існувала така стала, щобприі всіх.

Доведення. Оцінимо залишок у формі Лагранжа:

, оскільки лежить між 0 іх.

Тоді за теоремою про стиснуту змінну (п.5) .

Зауваження. З доведення випливає, що обмеження ,може бути ще послаблене.

272