151. Знакозмінні ряди. Абсолютна та умовна збіжність

Розглянемо ряд

Означення. Ряди, у яких є доданки як додатні, так і від`ємні, називають знакозмінними рядами.

Нехай ряд (1) - знакозмінний, тоді ряд (2)– знакододатний.

Означення. Якщо ряди (1) і (2) збігаються, то збіжність ряду (1) називається абсолютною. Якщо ряд (1) збіжний, а ряд (2) розбіжний, то збіжність ряду (1) називається умовною.

Теорема. Якщо ряд (2) збіжний, то ряд (1) збіжний абсолютно.

Доведення.

Розглянемо ряд (3): . Це знакододатний ряд, оскількиі рядзбіжний, то за ознакою порівняння збіжний і ряд (3). Розглянемо різницю збіжних рядів:-=. З пункту 142 різниця збіжних рядів є збіжним рядом.

152. Знакопочережні ряди. Ознака Лейбніца

Розглянемо ряд (1) , де.

- тут знаки чергуються.

Ознака Лейбніца

Якщо 1) ;

2) , тобто послідовністьмонотонно спадає, то ряд (1) збіжний.

Доведення.

-

послідовність частинних сум з парними номерами знакододатна і монотонно зростає.

Тобто , послідовністьобмежена числома₁.

За теоремою Вейєрштрасса . Оскільки, то

. Тоді і ряд (1) збігаються.

Зауваження.

1. , тобто послідовністьмонотонно спадає і обмежена знизу числомS. Тоді при.

Таким чином, .

Нехай знакозмінний ряд збігається до числа S. - залишок ряду..

збіжний знакозмінний ряд.

(див. попередній пункт, де ).

Таким чином, абсолютна величина залишку не перевищує модуля першого відкинутого члена: , тобто з цією точністю можна записати

.

Лекція 43

153. Основні властивості абсолютно й умовно збіжних рядів

Теорема Коші. Якщо ряд збігається абсолютно, то від перестановки його членів абсолютна збіжність і сума ряду не змінюються (без доведення).

Торема Римана. Якщо ряд збігається умовно, то, переставляючи його члени можна одержати розбіжний ряд або збіжний до кожного наперед заданого числа (без доведення).

Приклад до теореми Римана.

Ряд - умовно збігається, тобто(в п.183 доведено, що)

Переставимо члени цього ряду за правилом: за одним додатним ідуть два від`ємних.

(*)

Часткова сума отриманого ряду:

.

Таким чином, у результаті перестановки членів сума ряду змінилася (зменшилася вдвічі).

154. Функціональні ряди

Розглянемо послідовність функцій

Означення. Вираз називається функціональним рядом.

Означення. Якщо всі функції послідовності визначені в точцій числовий рядзбігається, то кажуть, що функціональний рядзбігається в точці.

Означення.Множина точок, у яких функціональний ряд збігається, називається областю збіжності функціонального ряду.

Приклад

при .

Таким чином, областю збіжності даного ряду є інтервал (-1;1) і ряд збігається до суми .

Часткова сума функціонального ряду:

.

Якщо ряд збігається до суми , то- залишок ряду також є функцією відx. Зауважимо, що .

Тобто якщо ряд збігається, то границя залишку цього ряду дорівнює нулю.

155. Мажоровані ряди. Рівномірна збіжність

Приклади

Розглянемо функціональний ряд (1) і збіжний знакододатний числовий ряд (2).

Означення. Якщо при виконуються нерівності, то ряд (1) називають мажорованим , а ряд (2)- мажоруючим.

Приклад.

, тому що , а ряд- збіжний числовий ряд, то ряд (1) мажорованим рядом (2).

Зауваження 1. Зі збіжності ряду (2) випливає збіжність ряду (3) при(за ознакою порівняння). Зі збіжності ряду (3) за теоремою про абсолютну збіжність випливає абсолютна збіжність ряду (1), якщо він знакозмінний. Або ж ряд (3) збігається з рядом (1), якщо ряд (1) знакододатний.

Зауваження 2. Якщо ряд збігається, то при , тобто, що при. Таким чином, для кожногоіснує свій номер.

Означення. Кажуть, що ряд збігаєтьсярівномірно на множині Х, якщо , що при, при.

Приклади.

Дослідити на рівномірну збіжність ряди:

а) ,

б) .

Часткова сума ряду пункту а):

при .

при .

Тобто , що при

або або,

тобто . Таким чином, ряд пункту а збігається нерівномірно,

де - ціла частина числа.

Часткова сума ряду пункту б):

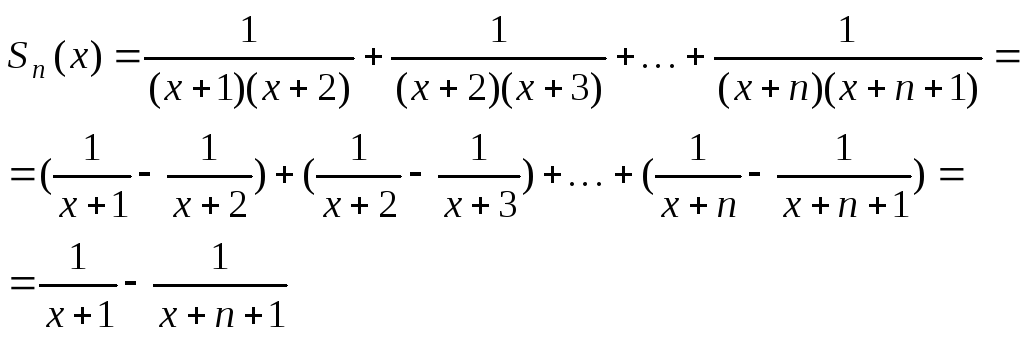
при .

при .

Тобто , що приабо

.

Оскільки іпри.

Таким чином, ряд пункту б збігається рівномірно.

156. Ознака Вейєрштрасса

Теорема. Якщо ряд (1) примажорується збіжним числовим рядом (2), то ряд (1) рівномірно збігається при.

Доведення

Зі збіжності ряду (2) випливає, що (- залишок ряду (2)). За визначенням границі:

, що при або

Оскільки ряд (1) мажорується, то він збігається абсолютно при (зауваження 1), тоді існує його сумай

.

при .

Отже,з нерівності (*) випливає, що залежить тільки від. Значить ряд (1) збігається рівномірно.

Зауваження

1. Мажорований ряд збігається абсолютно.

2. Ряд (3) так само мажорується рядом (2), тому він також рівномірно збігається.

3. Не будь-який рівномірно збіжний ряд збігається абсолютно.

4. Не для будь-якого рівномірно й абсолютно збіжного ряду (1) ряд (3) буде рівномірно збігатися.

Зауваження 3 і 4 стосуються немажорованих рядів.

Лекція 44

157. Геометрична інтерпретація рівномірної збіжності ряду

Нехай ряд (1) рівномірно збігається.

За визначенням рівномірної збіжності:

, що при , тобто остання нерівність виконується при.

.

Всі ( прий) лежать у смузі (), якщо ряд рівномірно збігається.