127. Обчислення поверхневого інтеграла за координатами

Оскільки інтеграл (*) (п. 125) складається із трьох інтегралів (**), то розглянемо обчислення одного з них, наприклад, .

Нехай - проста, незамкнена, гладка поверхня, задана рівнянням.

Тут - проекція поверхніна площину, а знак вибирається за «правилом косинусів».

Інші поверхневі інтеграли зводяться до подвійного аналогічним чином, тільки з рівняння поверхні виражається зміннаабо.

Приклад.

Обчислити інтеграл , де:.

Для обчислення подвійного інтеграла введемо узагальнену полярну систему координат:

.

.

Лекція 38

128. Спрощені формули зведення поверхневого інтеграла за координатами до подвійного

Нехай задана рівнянням.

,

;

;

.

Остаточно

.

Знак вибирається за «правилом косинусів». Переходимо до подвійного інтеграла:

.

Аналогічно записуються подвійні інтеграли, якщо поверхня задається рівняннямабо:

або

.

129 Застосування поверхневих інтегралів до задач геометрії й фізики (список формул)

1. Маса оболонки: , тут,- густина.

2. Площа оболонки: .

3. Статичні моменти оболонки щодо координатних площин:

,

,

.

4. Координати центра мас:

;

;

.

5. Моменти інерції:

, аналогічно визначаються ,.

, аналогічно визначаються ,.

- полярний момент інерції.

6. Потік рідини через поверхню :

.

7. Потік вектора через поверхню:

.

130. Скалярне поле. Лінії й поверхні рівня

Означення. Якщо в кожній точці області V задана скалярна величина , то кажуть, що на множині V задане скалярне поле.

Означення. Поле називається стаціонарним, якщо функція не залежить від часу t, тобто.

Для наочного зображення скалярного поля використовуютьлінії рівня:

, тут h – крок, n =1,2…...

Наприклад, топографічний план дає уявлення про кривизну поверхні .

Місця згущення ліній рівня кажуть про більш крутий підйом поверхні .

Для поля температур лінії рівня - лінії однакових температур, тобто «ізотерми».

Для поля тисків - «ізобари» - лінії однакових тисків.

Якщо , то рівністьдає рівнянняповерхонь рівня скалярного поля, або еквіпотенціальні поверхні, тобто поверхні рівного потенціалу.

Наприклад, потенціал електростатичного поля

, тобто поверхні рівня – концентричні сфери із центром в , де перебуває електричний заряд e.

131. Похідна за напрямком

Для вивчення скалярного поля потрібно в першу чергу досліджувати, як воно змінюється при переході від однієї точки до іншої, тобто в заданому напрямку

, де .

За визначенням похідної:

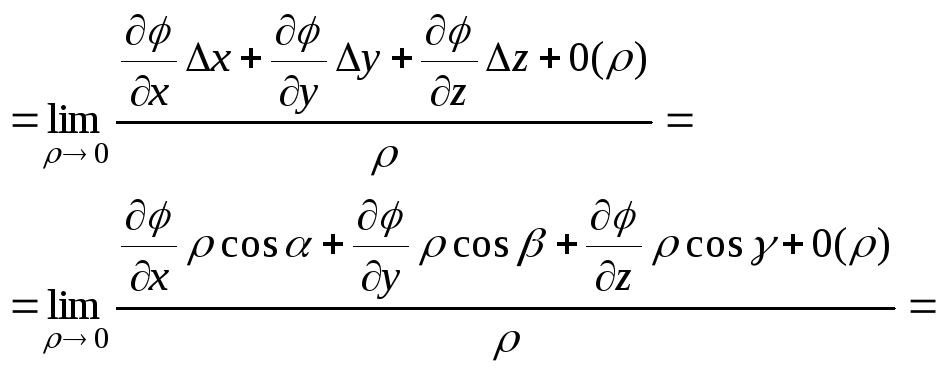
, або

де вектор - одиничний вектор, що вказує напрямок вектора.

Означення. Вектор називаютьградієнтом і позначають .

Зауваження:

1. Оскільки рівняння поверхні рівня , то вектор нормалі до цієї поверхні. А це і є. Аналогічно й для ліній рівня.

2. Оскільки , то найбільше значення, коли косинус дорівнює одиниці, тобто кут. Таким чином, напрямок- напрямок найшвидшого зростання функції.

Висновок:

Вектор спрямований по нормалі до лінії або поверхні рівня у бік найшвидшого зростання функціїй чисельно дорівнює швидкості зміни функції у цьому напрямку. Щоб визначити швидкість зміни функціїв іншому напрямку, досить спроектуватина цей напрямок.

Лекція 39

132. Векторне поле. Векторні лінії

Означення. Якщо в кожній точці області V заданий вектор , то кажуть, що в області V задане векторне поле.

Означення. Лінія, у кожній точці якої напрямок дотичної збігається з напрямком поля, називається векторною, або силовою лінією.

Нехай ~або

.

Дотичний вектор до лінії :.

Оскільки , то за визначенням силової лінії

Отримана система диференціальних рівнянь визначає векторну лінію, тобто розв`язок цієї системи дасть рівняння векторної лінії L.

133. Циркуляція векторного поля

Означення. Роботу векторного поля уздовж замкненого контура L називаютьциркуляцією векторного поля: .

Приклад. Нехай рідина обертається зі сталою кутовою швидкістю навколо осі. Визначити циркуляцію поля лінійних швидкостей.

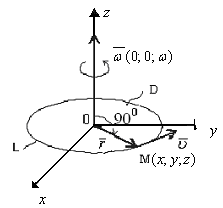
Розглянемо поле лінійних швидкостей обертового потоку рідини . Визначимо циркуляцію :

Тут використовувалася формула Гріна, - площа області. Ясно, що циркуляція характеризує обертовий рух векторного поля.

134. Ротор векторного поля

Означення. Вектор називаютьротором (вихром) векторного поля

й позначають

Приклад. Визначити ротор поля лінійних швидкостей обертової рідини навколо осі , якщо. Оскільки, то

тобто ротор поля лінійних швидкостей так само, як і циркуляція, характеризує обертовий рух поля.

135. Формулювання теореми Стокса

Циркуляція векторного поля

уздовж замкненого контура дорівнює потоку ротора цього поля через поверхню, натягнуту на контур.

Таким чином, якщо

,

то - теорема Стокса у векторній формі. Тут- одиничний вектор нормалі до поверхні

При обході контура проти ходу годинникової стрілки поверхняувесь час залишається ліворуч.

Теорема Стокса в координатній формі :

=.

Зауваження. Розглянемо плоске векторне поле , задане на точках плоскої областііз границею, тоді формула Стокса набере вигляду:, тому що,,. А це є формула Гріна, доведена в пункті 118.

136. Дивергенція векторного поля. Формулювання теореми Остроградського - Гауса

Означення. Скалярну величину називаютьдивергенцією (розбіжністю) векторного поля й позначають.

Теорема Остроградського-Гауса.

Потрійний інтеграл від дивергенції векторного поля за об'ємомдорівнює потоку цього поля через поверхню, що обмежує цей об'єм.

Таким чином, якщо , то- теорема Остроградського - Гауса у векторній формі. Тут- одиничний вектор нормалі до зовнішньої сторони поверхні.

Лекція 40

137. Фізичний зміст дивергенції векторного поля

Зауважимо, що якщо потік векторного поля через замкнену поверхню більше нуля, то витікає рідини більше, ніж втікає, тобто в областіє джерела.

Якщо , то є стоки, якщо ж, то скільки втікає, стільки й витікає.Щоб дослідити на наявність джерел або стоків у точці , розглянемо дельта-окіл точки й ,тобто дельта-окіл стягується в точку .

Отже, 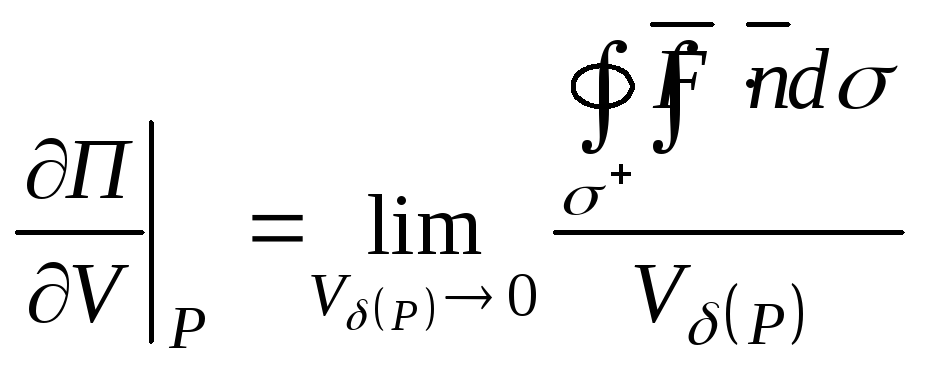(за теоремою Остроградського-Гауса) (за теоремою про середнє) = , тому що.

Тоді характеризує наявність джерел і стоків у точці, причому, якщо:

, то в точці джерело,

, то в точці стік,

, то в точці немає ні джерел, ні стоків.

138. . Доведення теореми Остроградського-Гауса

Теорема Остроградського - Гауса в координатній формі: якщо  правильна тривимірна область, обмежена замкненою поверхнеюй для векторного поля.

, то

.

Доведення

Розглянемо

Зауважимо, що , тому що нормальний векторутворить тупий кут з віссюй, а, тому що.

Аналогічно визначаються

й .

Отже,.

139. Потенційне поле і його основна властивість

Означення. Векторне поле називаєтьсяпотенційним, або безвихровим, якщо для .

Якщо

- умови потенційності векторного поля.

З теореми Стокса випливає, що по будь-якому замкненому контуру, тоді за аналогією із плоским випадком (п. 119), підінтегральний вираз в криволінійному інтегралі є повним диференціалом деякої функції.

Тут функція визначається за формулою:

Означення. Функція називаєтьсяпотенціалом векторного поля.

Оскільки то.

Таким чином, у потенційному полі

Основна властивістьпотенційного поля полягає в тому, що робота в потенційному силовому полі не залежить від шляху інтегрування, а дорівнює різниці значень потенціалу в кінцевій і початковій точках.

Доведення.

140. Соленоїдальне поле і його основна властивість

Означення. Векторне поле називаєтьсясоленоїдальним, або трубчастим, якщо для .

Основна властивість

У соленоїдальному полі потік вектора через будь-яку замкнену поверхню дорівнює нулю.

Доведення

.

141. Гармонічне поле і його основна властивість

Означення. Векторне поле називаєтьсягармонійним, якщо воно потенційне й соленоїдальне одночасно, тобто ,.

Оскільки , то, тоді

.

 рівняння Лапласа.

Означення. Якщо функція двічі неперервно диференційована й задовольняє рівняння Лапласа, то її називають гармонічною.

Основна властивістьгармонійного поля полягає в тому, що потенціал гармонійного поля є функцією гармонічною.

Означення. Вектор називають оператором Гамільтона, або набла-вектором.

1) ;

2) =;

3) .

Лекція 41

142. Числові ряди. Основні поняття

Розглянемо нескінченну числову послідовність .

Означення. Вираз називають числовим рядом, а суму першихдоданків– частковою сумою ряду.

Означення. Якщо , то кажуть, що ряд збігається до числай сума ряду дорівнює. Якщо жабо не існує, то кажуть, що ряд розбігається.

Приклад.

; ;, тобто даний ряд розбігається.

Теорема. Якщо , а ряди,збігаються, то рядийтак само збігаються.

Доведення

1) і, десума ряду. Таким чином,;

2) ,. Отже, рядзбігається до суми.

143. Геометрична прогресія

Складемо ряд із членів геометричної прогресії:

(*). ;, якщо, то, і отже, ряд (*) збігається до числа. Якщо ж, тодорівнює нескінченності або не існує й ряд (*) розбігається.

144. Необхідна ознака збіжності

Теорема. Якщо ряд збігається, то.

Доведення.

,

,

.

Зауваження. Якщо , то рядможе бути як збіжним, так і розбіжним, але якщо, то рядрозбіжний.

145. Ряди з додатними членами. Ознаки порівняння

Розглянемо ряд з додатними членами ,. Оскільки, то послідовність часткових сум зростає йабо, причому, якщо послідовність часткових сум обмежена зверху .

Теорема

Дано два ряди з додатними членами ,і. Тоді зі збіжності рядувипливає збіжність ряду, з розбіжності рядувипливає розбіжність ряду.

Доведення.

1), тому що рядзбігається, той послідовністьобмежена числом. Тоді за теоремою Вейєрштрасса вона має скінченну границю.

2) Якщо ряд розбігається, той, тобтой рядтакож розбігається.

146. Гранична форма ознаки порівняння

Дано два ряди з додатними членами й , дей, тоді або обидва ряди збігаються, або обидва розбігаються.

Доведення

За визначенням границі: такий, що при, тобтоабо. Інше випливає з теореми п. 145.

147. Ознака Даламбера

Якщо для ряду з додатними членами , то прирядзбігається, прирядрозбігається, припотрібні інші дослідження.

Доведення

1. ,

тобто знайдеться такий номер , що при

Ряд - збігається як нескінченно спадна геометрична прогресія. Тоді за ознакою порівняння (п.145) збігається ряд. Останній ряд відрізняється від рядуна скінченне число перших доданків, тобто він також збігається, хоча суми їх і різні.

2. ,

тобто знайдеться такий номер , що при, тобто послідовністьмонотонно зростає. Тодій за зауваженням до необхідної ознаки рядрозбігається.

148. Радикальна ознака Коші

Якщо для ряду , то прирядзбігається, прирядрозбігається, припотрібні інші дослідження.

Доведення

1. ,

тобто знайдеться такий номер , що при

Ряд - збігається як нескінченно спадна геометрична прогресія. Тоді збігається й ряд. Рядвідрізняється від рядуна скінченне число перших доданків, тому він також збігається.

2. ,

тобто знайдеться такий номер , що прий. Отже, рядрозбігається.

Лекція 42

149. Інтегральна ознака Коші

, і монотонно спадає. Тодіізбігаються або розбігаються одночасно.

Доведення

тобто площа нижньої східчастої фігури (заштрихованої) менше площі криволінійної трапеції, яка, у свою чергу, менше площі верхньої східчастої фігури.

, де

,, таким чином,

(*)

(**)

1. збігається до числаІ, тобто . Послідовністьмонотонно зростає і обмежена зверху числом(див. (**)). Тоді за теоремою Вейєрштрасса послідовністьмає скінченну границю і рядзбіжний.

2. , тобто розбігається. Отже,. Переходимо у нерівності (*) до границі:, тобто, або рядрозбіжний.

150. Узагальнений гармонічний ряд

Означення. Ряд , де, називається узагальненим гармонічним рядом.

Розглянемо .

1. , тоді

, тобто інтеграл розбіжний.

2. , тоді

, тобто інтеграл також розбіжний.

3. , тоді

, тобто інтеграл збіжний.

Тоді за інтегральною ознакою Коші ряд