Розв`язання типового варіанта обов'язкового домашнього завдання №1

1. Обчислити границі числових послідовностей:

а) ;

б) ;

в) ;

г) .

Оскільки у границі пункту а) маємо невизначеність , то в чисельнику виносимо за дужки старший степінь, а в знаменникуn

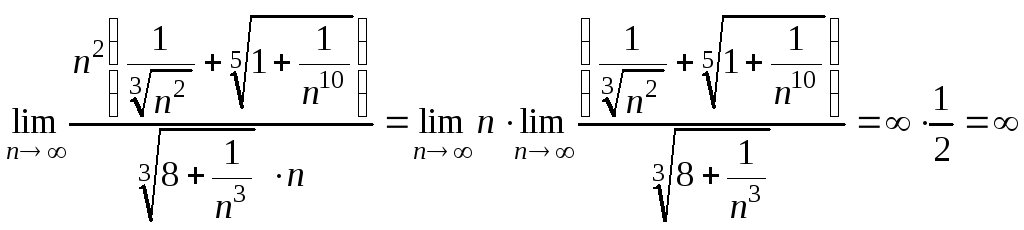
У границі чисельника пункту б) маємо невизначеність , чисельник і знаменник множимо на спряжений вираз

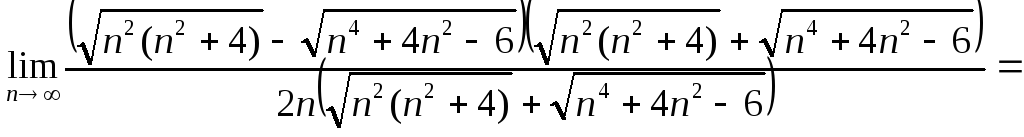
При обчисленні границі пункту в) скористаємося формулою , оскільки числа 2, 4, … , 2n утворять арифметичну прогресію, де , тоді

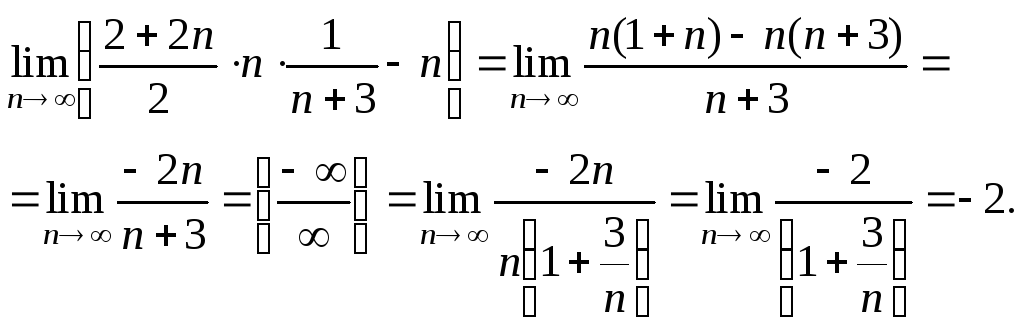
Перш ніж обчислювати границю пункту г), визначимо границю основи степеня:

.

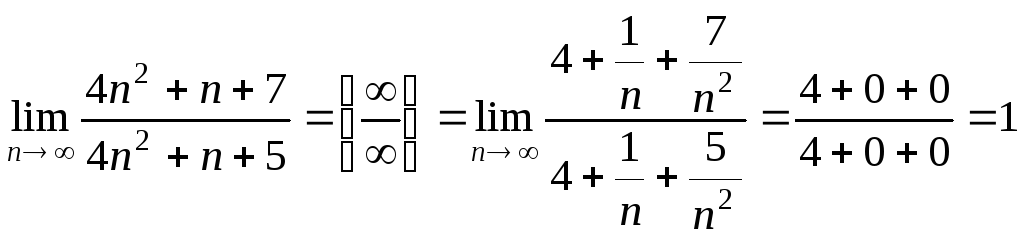Таким чином, .

Зробимо деякі істотні перетворення:

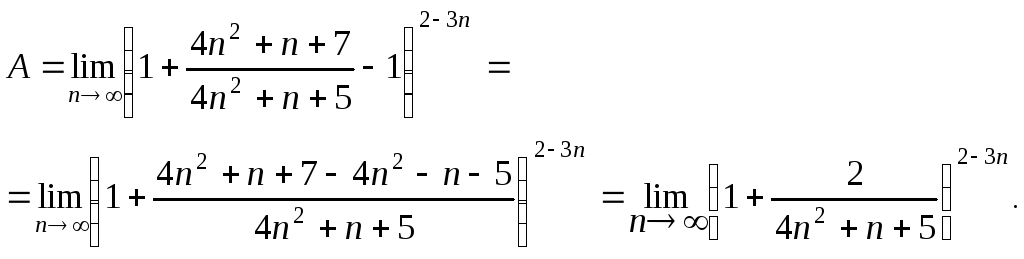
1-й спосіб. Скористаємося другою важливою границею у вигляді , тоді

=

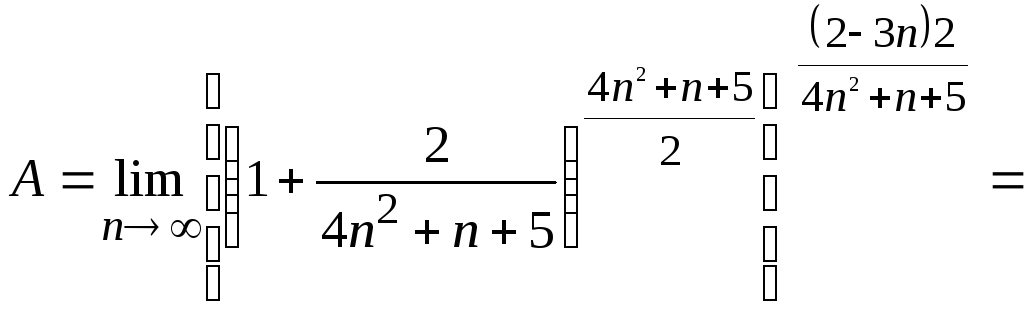
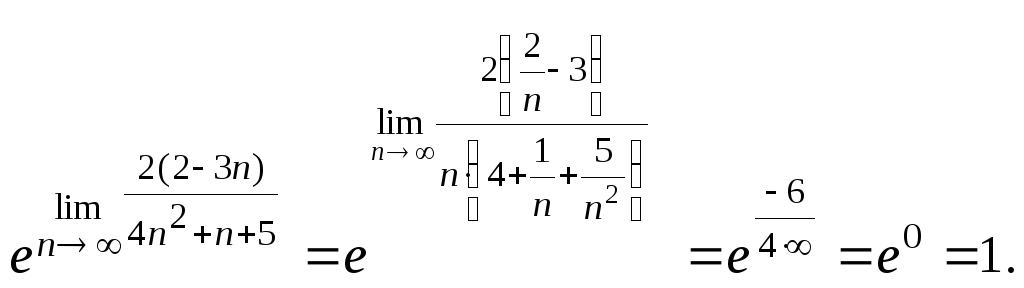
Тут ,.

Отже, .

2-й спосіб. Скористаємося формулою й таблицею еквівалентних. Тоді

Тут при(~ - знак еквівалентності).

2. Довести, що ,тобто за заданим визначити. Якщо,

то за визначенням границі функції , що при,, тоді

.Отже,

(Скорочення на було справедливе, тому що у визначенні).

3. Використовуючи таблицю еквівалентних, обчислити границі функцій:

а)

б)

в)

г)

д)

Дві нескінченно малі величини називаються еквівалентними, якщо границя їх частки дорівнює одиниці, наприклад, приабопри. Тоді

- після заміни на еквівалентні величини.

Скорочуючи на х, одержимо

У границі пункту б скористаємося еквівалентними й~при.

Таким чином,

=

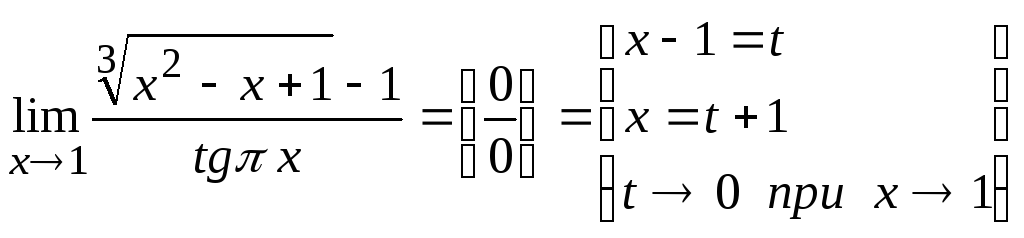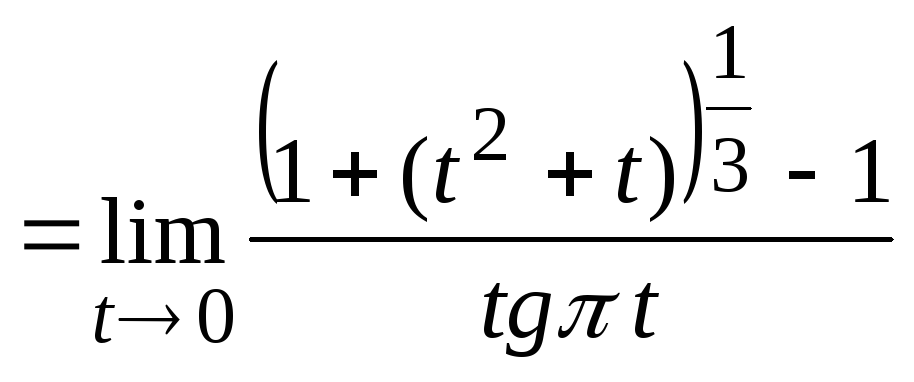(за формулами зведення ).

Чисельник і знаменник замінимо на еквівалентні величини:

.

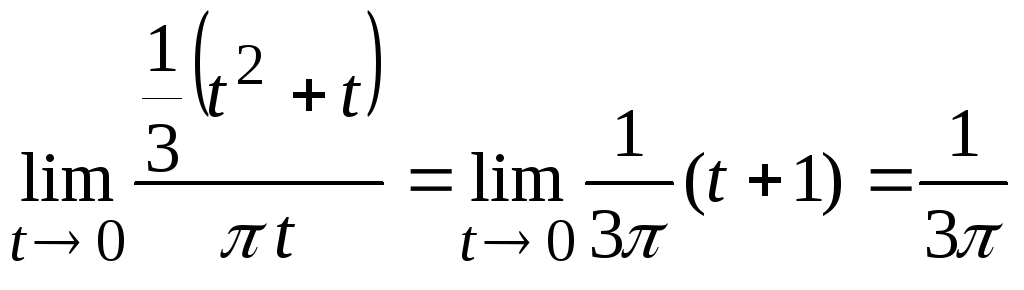Обчислимо .

Виділимо в основі степеня одиницю:

(див. 2-й спосіб розв`язання прикладу 1г).

Тепер скористаємося таблицею еквівалентних величин

Розглянемо приклад г:

Оскільки, то

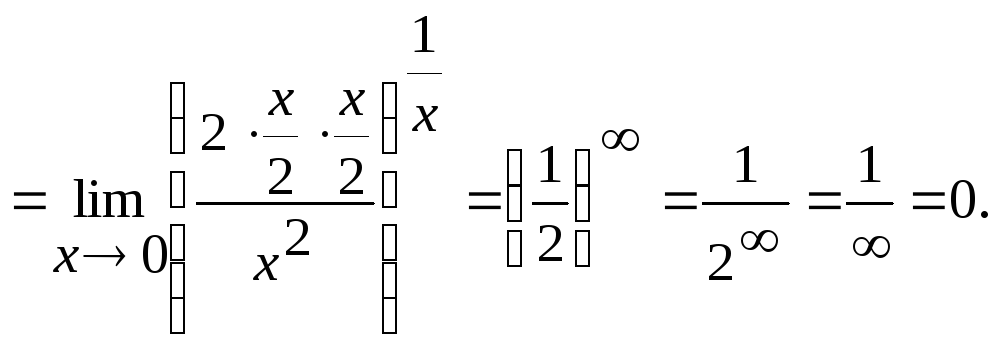
Розглянемо приклад д

.

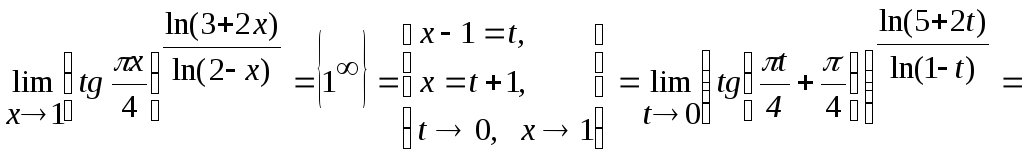
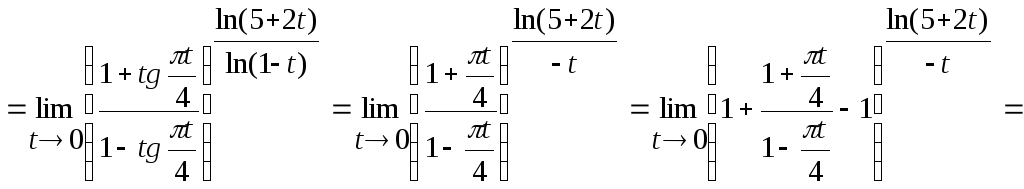
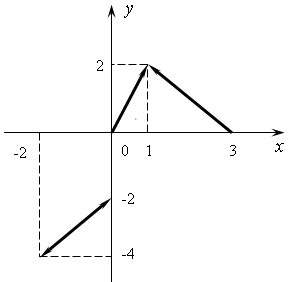
4. Дослідити дану східчасту функцію на неперервність і побудувати її графік, якщо

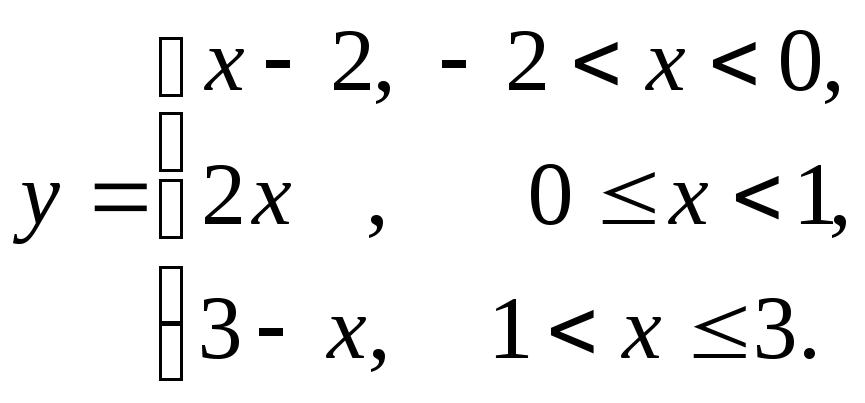
Функції неперервні у відповідній області завдання, отже, розрив може бути тільки в точках переходу від одного аналітичного вираження до іншого. Тому досліджуємо тільки точки прий.

а) ,

,

.

Оскільки , але обидві скінченні, то в точці зрозрив 1-го роду, стрибок функції.

б) .

.

, але функція при не визначена, тобто в точці зусувний розрив.

5. Виходячи з визначення похідної, знайти , якщо

.

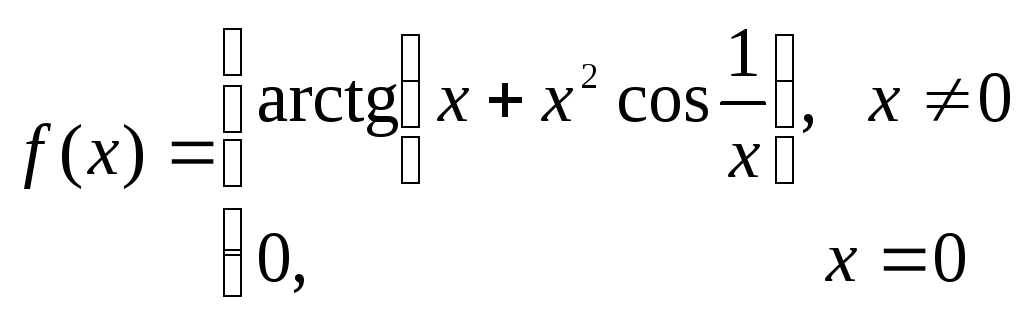За визначенням, якщо існує, то вінназивається похідною функцією в точці x₀ й позначається .

.

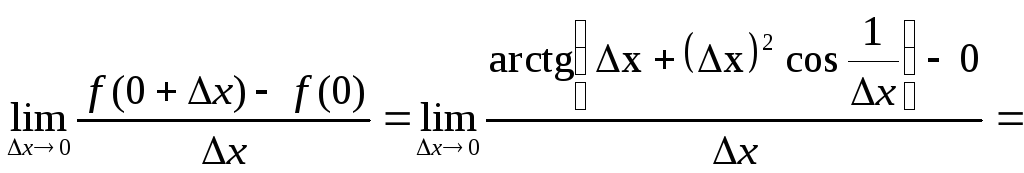
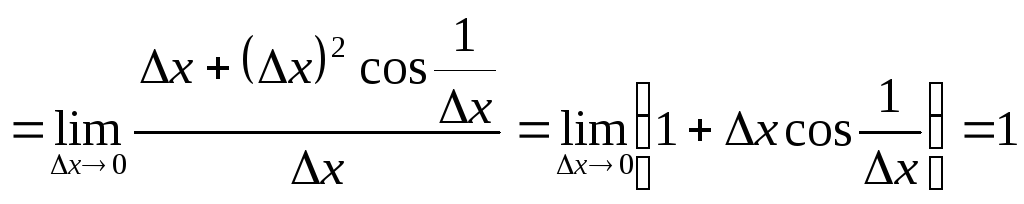Оскільки за теоремою, якщо нескінченно малу функцію помножити на обмежену, то одержимо нескінченно малу, .

6. Знайти похідні таких функцій:

а) ;

б) ;

в) ;

г) .

а) Оскільки і, то

У прикладі пункту б помітимо, що , а.

Тому , а оскільки, то

.

У прикладі пункту в застосовуємо метод логарифмічного диференціювання. Прологарифмуємо функцію :

.

Продиференціюємо ліву й праву частини:

,

або .

Для закріплення матеріалу розв’яжемо приклад г:

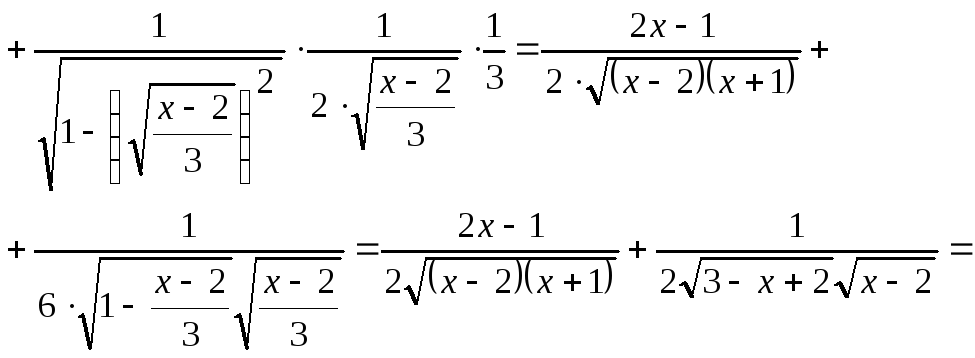
Зауваження. Щоб відпрацювати методи визначення похідних і не ускладнювати цей матеріал, ми не враховуємо ОДЗ (область допустимих значень) для функції й похідної. Ясно, що результати обчислень справедливі тільки для всіх , де множина Х – загальна частина ОДЗ функції й ОДЗ отриманої похідної.