Розв`язання типового варіанта обов'язкового домашнього завдання 3

1. Довести збіжність ряду й знайти його суму:

.

Для доведення збіжності ряду використовуємо граничну форму ознаки порівняння двох знакододатних рядів (1) і (2), з якої випливає, що якщо, то ряди або одночасно збігаються, або одночасно розбігаються.

Отже, ми маємо ряд (1) і ряд (2).

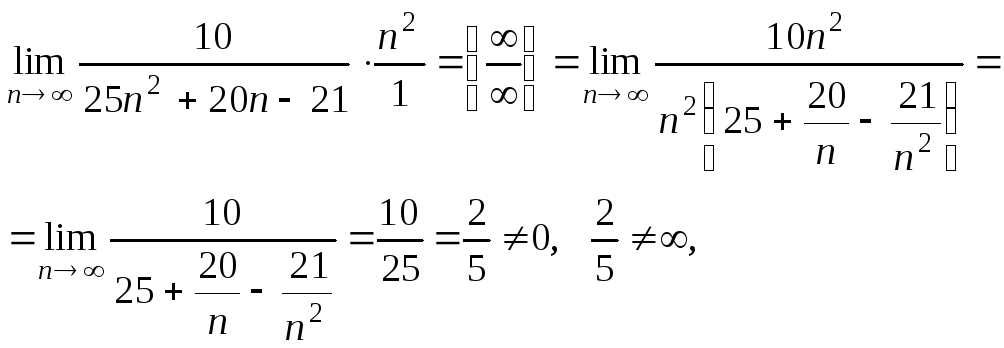
а оскільки ряд (2) збігається як узагальнений гармонічний ряд з 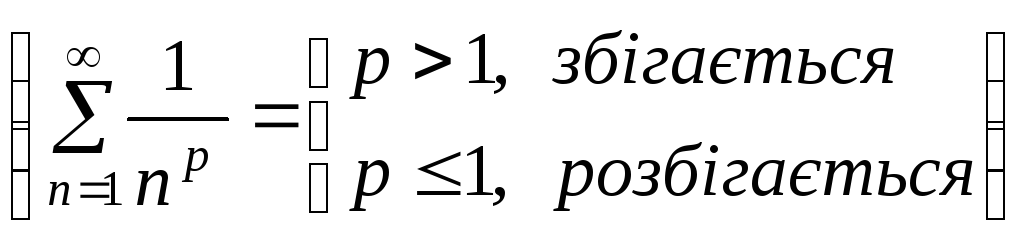, то ряд (1) також збігається.

Щоб знайти суму ряду, скористаємося визначенням: якщо , то кажуть, що ряд збігається й S називається сумою ряду, якщоабо не існує, то кажуть, що ряд розбігається. Тут S_n – сума n перших членів ряду, тобто часткова сума. У нашому випадку

(щоб розкласти дріб на суму найпростіших, потрібно застосувати метод невизначених коефіцієнтів).

Тоді

(ці доданки не мають подібних).

Таким чином, сума ряду .

2. Дослідити на збіжність ряди з додатними членами:

а) ; б);

в) ; г).

У прикладі пункту а використовуємо ознаку Даламбера.

, а оскільки , то за ознакою Даламбера даний ряд збігається.

У прикладі пункту б використовуємо радикальну ознаку Коші.

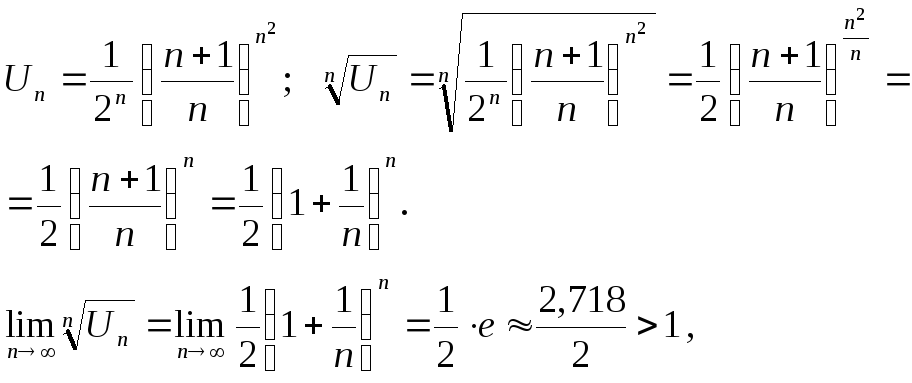
тоді за радикальною ознакою Коші ряд розбігається.

У прикладі пункту в використовуємо граничну форму ознаки порівняння.

Для порівняння візьмемо ряд

Оскільки , то зі збіжності рядувипливає збіжність ряду

У прикладі пункту г використовуємо граничну форму ознаки порівняння й інтегральну ознаку Коші, тобто

порівнюємо з рядом , тому що

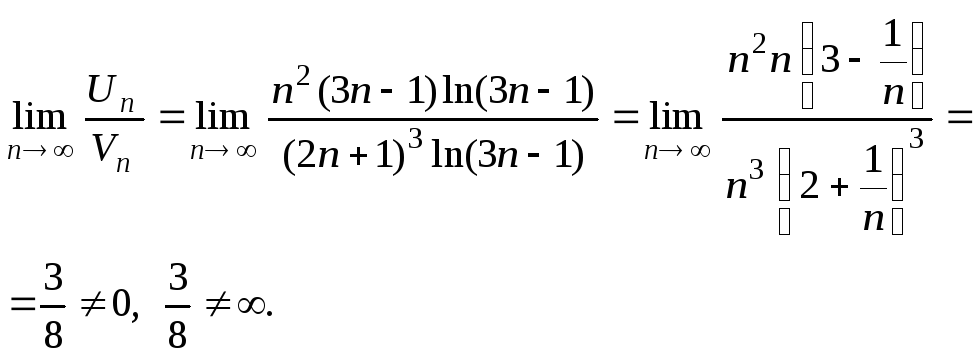
Зауважимо, що послідовність спадає, тоді до ряду (2) застосуємо інтегральну ознаку Коші:

.

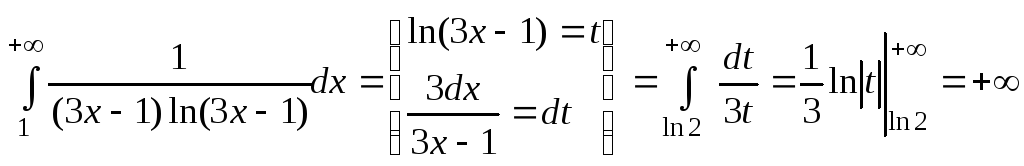Оскільки інтеграл розбігається, то розбігається ряд (2), а з розбіжності ряду (2) випливає розбіжність ряду (1).

3. Дослідити на умовну й абсолютну збіжність ряди зі знакопочережними членами:

а) ; б).

Оскільки ряд (2) знакосталий, то застосуємо до нього радикальну ознаку Коші:

.

і ряд (2) збігається. Тоді за теоремою про абсолютну збіжність ряд (1) збігається, причому абсолютно.

У прикладі пункту б) ряд (1) ,

ряд (2) . Ряд (2) знакосталий, тому можна застосувати граничну форму ознаки порівняння. Для порівняння беремо ряд (3), тому що

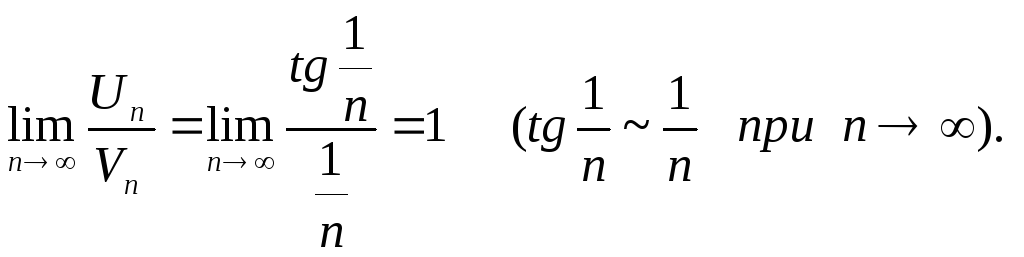
Але ряд (3) розбігається (гармонічний ряд розбігається – легко перевірити за інтегральною ознакою Коші).

З розбіжності ряду (3) випливає розбіжність ряду (2). Тоді ряд (1) або розбігається, або умовно збігається. До ряду (1) застосовуємо ознаку Лейбніца:

, якщо

а)

б) для досить великих n, то знакопочережний ряд збігається.

а)

б) оскільки , а функція y = tg x зростаюча, топри всіх n.

Отже, ряд (1) збігається, причому умовно.

4. Використовуючи необхідну ознаку збіжності ряду, довести справедливість рівності

.

Розглянемо ряд , дослідимо його на збіжність за ознакою Даламбера.

.

.

Тут

Оскільки, то ряд збігається. За необхідною ознакою якщо ряд збігається, то. Що й було потрібно довести.

5. Знайти область збіжності для таких функціональних рядів:

а) ;

б) ;

в) .

(1) ; (2).

До ряду (2) застосуємо ознаку Даламбера:

.

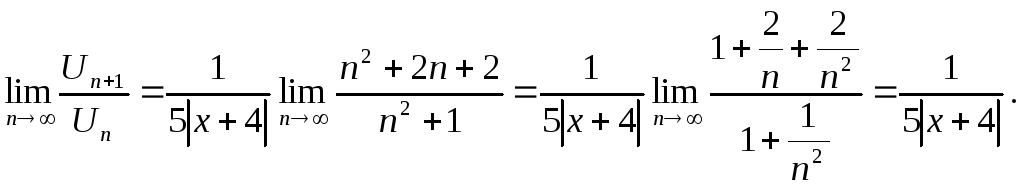
Ряд (2) збігається, якщо .

Тоді або

Ряд (1) при знакопочережний, за теоремою про абсолютну збіжність він збігається, причому абсолютно.

Досліджуємо ряд (1) на кінцях області збіжності.

Нехай x = – 3,8, тоді

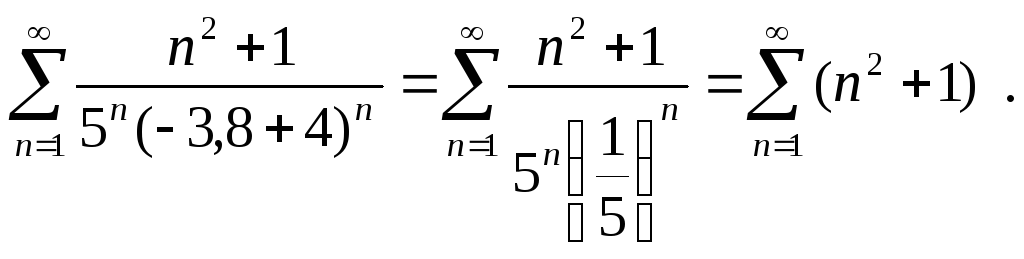
Оскільки , тобто не дорівнює нулю, то за наслідком до необхідної ознаки ряд розбігається.

Нехай x = – 4,2 , тоді

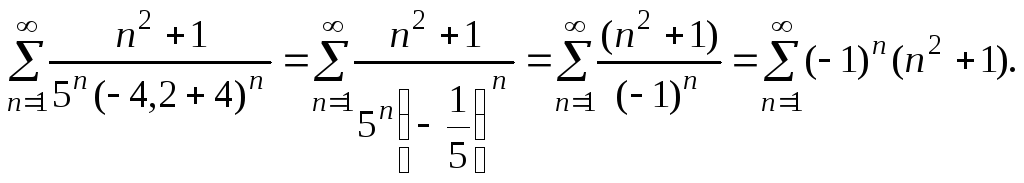
Перша умова ознаки Лейбніца не виконується, ряд розбігається.

Висновок

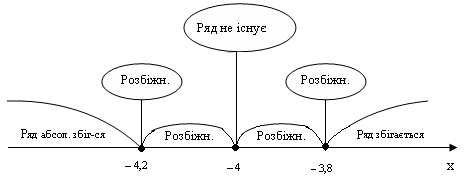
У прикладі пункту б зробимо заміну змінних cos x = y, одержимо ряд (1) ; (2).

До ряду (2) застосуємо ознаку Даламбера:

.

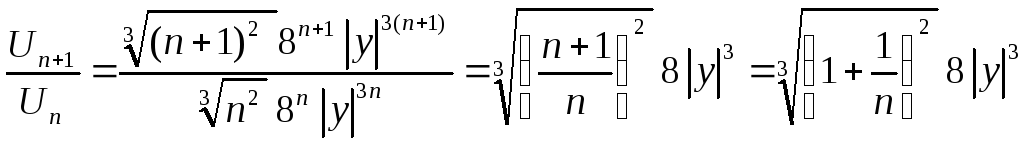
Ряд (2) збігається, якщо або.

Дослідимо ряд (1) на кінцях області збіжності.

Нехай , тоді.

Оскільки , то ряд (1) прирозбігається.

Нехай , тоді– ряд знакопочережний, перша умова ознаки Лейбніца не виконується, ряд розбігається.

Таким чином, область збіжності ряду (1) ,

отже, .

Розв`язування тригонометричної нерівності:

–oбласть збіжності ряду

У прикладі пункту в зробимо заміну змінних , одержимо знакододатний ряд

, застосуємо радикальну ознаку Коші:

.

Ряд (2) збігається, якщо , тобто.

Дослідимо ряд (1) на кінцях області збіжності у = 1. Одержимо ряд , що розбігається, тому що(не виконується необхідна ознака).

Таким чином, область збіжності ряду . Визначимо область збіжності даного ряду, розв’язуючи нерівність:. Оскількито. Отже,.

Висновок