158. Неперервність суми ряду

Теорема. Якщо ряд (1) , складений з неперервних на інтерваліфункцій, рівномірно збігається до суми, то.

Доведення.

Оскільки абой(як сума скінченного числа безперервних функцій), то залишається довести, що. Доведемо, що, тобто, що при.

З рівномірної неперервності випливає: , що прийабоприй.

Зафіксуємо n. ;

при й, отже і при.

159. Почленне інтегрування рядів

Теорема. Якщо ряд (1) , складений з неперервних на множиніфункцій, рівномірно збігається до суми, то, тобто ряд можна почленно інтегрувати на цьому відрізку.

Доведення.

Для ряду (1)

. , тому що всі функції неперервні (за теоремою пункту 158 ).

Визначимо суму ряду (2) . Часткова сума ряду (2):. Визначимо

.

Оскільки ряд (1) рівномірно збігається, то , що при.

Тоді при. Отже,й, тобто ряд (2) збігається і його сума є.

160. Почленне диференціювання рядів

Теорема. Нехай функції визначені в проміжку, неперервно диференційовані там і ряд (1)збігається до. Якщо ряд (2)рівномірно збігається, тодиференційована й сума ряду (2) дорівнює.

Доведення

Оскільки і, то- за теоремою з пункту 142.

Ряд (2) рівномірно збігається до S⁽²⁾(x), отже, його можна почленно інтегрувати (теорема п.159) на :

Отже, . Ліва частина рівності є функцією диференційованою, тоді й права частина – диференційованою, тобто

.

Таким чином, при виконанні умов даної теореми припустиме почленне диференціювання ряду.

Лекція 45

161. Степеневі ряди. Теорема Абеля

Ряди вигляду або, де- сталі числа, називаютьсястепеневими.

Теорема Абеля. Якщо степеневий ряд (1) збігається при, то він абсолютно збігається при, що задовольняють нерівність. Якщо ряд (1) розбігається в точці, то він розбігається при.

Доведення.

1. Оскільки ряд збігається, топри.

.

Ряд збігається при(як ряд, що складається із членів геометричної прогресії). Тоді за ознакою порівняння збігається ряд (2)при. А за теоремою про абсолютну збіжність (пункт 151) ряд (1) збігається, причому прийзбігається абсолютно.

2. Другу частину теореми доведемо методом від супротивного: ряд (1) збігається в точці, тоді за першою частиною доведення ряд (1) збігається в точці, що суперечить умові. Отже, при, для яких, ряд розбігається.

162. Область збіжності

Зауваження до теореми Абеля. 1. Ряд (1) завжди збігається в точці .

2. Оскільки ряд може або збігатись або розбігатись, то всі точки числової осі розпадуться на симетричні (за теоремою Абеля) інтервали збіжності й розбіжності.

А оскільки третього не дано, проміжки збіжності й розбіжності мають загальну границю, що називається радіусом збіжності .

-R

0

R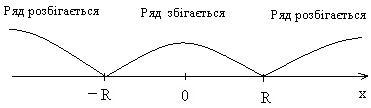

У точках ряд може як збігатися, так і розбігатися, для встановлення цього факту потрібні додаткові дослідження.

Приклад.

Ряд (1) , оскількиможе бути як додатним,

так і від`ємним, то спочатку розглянемо ряд (2) - знакододатний ряд. За ознакою Даламбера.

Якщо , то ряд (2) збігається; якщо, то ряд (2) розбігається. Радіус збіжності ряду (1).

Досліджуємо поводження ряду (1) на кінцях області збіжності.

1. , ряд (1) набере вигляду. Це гармонійний ряд 1, він розбігається.

2. , ряд (1)умовно збігається, тому що обидві умови ознаки Лейбніца виконуються, а рядрозбігається.

Таким чином, область збіжності ряду (1): [-1;1).

Зауваження.

Область збіжності ряду (1) може бути кожним з інтервалів [-R;R], (-R;R), [-R;R), (-R;R].

163. Рівномірна збіжність степеневого ряду

Теорема. Степеневий ряд (1) мажорується на будь-якому відрізку [], деінтервал збіжності ряду (1).

Доведення.

R – радіус збіжності ряду (1)

Ряд розбігається

, тоді числовий ряд (2) також збігається. Оскількипри, то ряд (2) є мажоруючим стосовно ряду (1) на.

Зауваження.

З ознаки Вейєрштрасса (п. 156) випливає, що ряд (1) рівномірно збігається на будь-якому відрізку , деінтервал збіжності ряду (1).

164. Почленне інтегрування степеневих рядів

Оскільки степеневий ряд (1) рівномірно збігається на , то сума рядуй такий ряд можна почленно інтегрувати на цьому відрізку (див. пункти 158, 159).

Приклад

Ряд (1)

при або.

Почленно проінтегруємо цей ряд на відрізку , де:

або

=.

Таким чином, при.

У п.183 доведено, що даний ряд збігається, якщо х=1.

165. Почленне диференціювання степеневих рядів

Теорема. Степеневий ряд (1) можна почленно диференціювати в будь-якій точці інтервалу збіжності (-R;R). Тут R - радіус збіжності ряду (1).

Доведення.

Розглянемо ряд (1) і ряд (2).

Визначимо області збіжності цих рядів:

1)

Таким чином, радіуси збіжності цих рядів збігаються. Оскільки степеневий ряд (2) збігається на інтервалі , то він рівномірно збігається на будь-якому відрізку(пункт163). Тоді за теоремою пункту 160 ряд (1) можна почленно диференціювати в будь-якій точці, тобто сума ряду (2). А оскільки будь-яку внутрішню точкуінтервалуможна укласти в інтервал, то наша теорема справедлива для.

Лекція 46

166. Ряди Тейлора й Маклорена. Теорема про єдине розкладання функції в степеневий ряд

Означення. Кажуть, що функція розкладається в степеневий ряд на інтервалі, якщо на цьому інтервалі ряд збігається і його сума дорівнює:.

Теорема (про єдине розкладання функції в степеневий ряд).

Нехай функція намає похідні всіх порядків і розкладається в степеневий ряд (1)(тобтопри, де). Тоді всі його коефіцієнти визначаються за формулами.

Доведення

З пункту 165 випливає, що ряд можна почленно диференціювати в середині області збіжності.

………………………………… ..……………………………….

…………… ……………..

………………… ………………

Отже, розкладання функції в степеневий ряд єдине. Тобто якщо функцію можна розкласти в степеневий ряд (1), що збігається до неї, то цей ряд має вигляд

і його називають рядом Маклорена.

Можливо, функція подана рядом за степенями:

– такий ряд називається рядом Тейлора.

167. Достатня умова розкладності функції в ряд Тейлора

Чи справджується обернене твердження, якщо нескінченно диференційована най для неї формально побудований ряд Тейлора, чи буде він збігатися наі його сума дорівнювати? У загальному випадку немає. З формули Тейлора (пункт 40) маємо. Перейдемо до границі при:.

Ясно, що сума ряду Тейлора збігатиметься з функцією, якщо.

Теорема (достатня умова) Якщо всі похідні приобмежені тим самим числом М, томоже бути подана рядом Тейлора на інтервалі.

Доведення

.

Оскільки , то, за теоремою про проміжну функціюі. *)

168. Розкладання в ряд Маклорена деяких функцій

Функція , а також усі їхні похідні обмежені за абсолютною величиною одиницею, тому їх можна подати рядом Маклорена:

, .

Ці розкладання справедливі при всіх .

*) Для розкладу функції в ряд Тейлора умову обмеженості похідних можна замінити менш обтяжливою умовою їх степеневого росту (див. п.184)

Функція й всі її похідні обмежені числомпри всіх, тому можна записати, що, оскільки

при кожному , то це розкладання справедливе при всіх.

Розглянемо деякі функції, розкладання яких у степеневі ряди можна одержати, використовуючи теорему про почленне інтегрування рівномірно збіжних рядів.

Оскільки і(неcкінченно спадна геометрична прогресія, туті, тобто). Ряд почленно проінтегруємо:

(*) при . За ознакою Лейбніца останній ряд умовно збігається при. Можна довести, що при, сума цього ряду дорівнює. Остаточно розкладання (*) справедливе при всіх.

Аналогічно міркуючи, одержимо:

169. Біноміальний ряд

Нехай , де,- будь-яке дійсне число.(*). Шукаємо розв`язок диференціального рівняння (*) у вигляді степеневого ряду. Оскількиі, то.

або .

Прирівнюємо коефіцієнти при однакових степенях . Пристоять коефіцієнтиабо.

Таким чином, маємо ,,

, , …,... .

Остаточно .

Визначимо область збіжності ряду за ознакою Даламбера:

якщо , то ряд збігається.

Зауваження

Можна довести, що при йотриманий ряд абсолютно збігається; прийряд збігається умовно.

Лекція 47

170. Розкладання функції в ряд Маклорена

Оскільки

Тут використовували біноміальний ряд і теорему про почленне інтегрування степеневого ряду. Використовуючи формулу Стірлінга для подвійних факторіалів, одержуємо, що ряд збігається при всіх .

171. Таблиця розкладань деяких функцій у ряд Маклорена

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

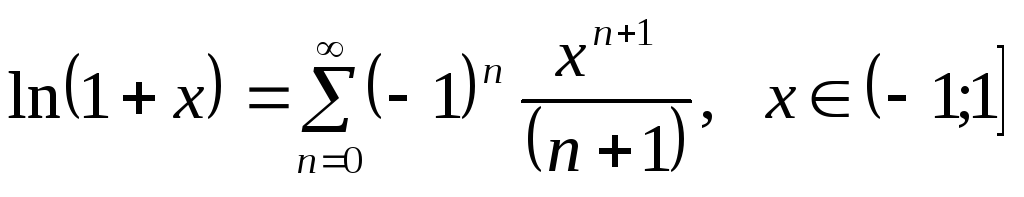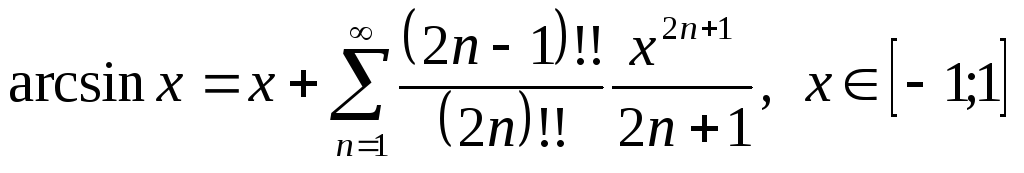172. Застосування степеневих рядів

1. Визначити числове значення з точністю до. Використовуємо розкладання.

Щоб визначити кількість доданків, оцінимо залишок:

Таким чином, і

.Точними є перші три цифри, остання - сумнівна.

2. Обчислити визначений інтеграл з точністю.

Використовуючи зауваження до ознаки Лейбніца, за заданою точністю визначимо кількість доданків.

при , тобто

,

.

Таким чином, , тобтоможна відкинути й

.

Точними є перші п'ять цифр.

3. Розв’язати диференціальне рівняння з початковими умовами

Шукаємо розв`язок у вигляді ряду Маклорена

Оскільки , то;, то; і т.д.

Зауважимо, що ,. Таким чином,

- частинний розв`язок даного диференціального рівняння, що задовольняє дані початкові умови.

173. Підсумовування степеневих рядів методом почленного інтегрування й диференціювання

Приклади

1.Визначити суму ряду (1).

(2)

;

.

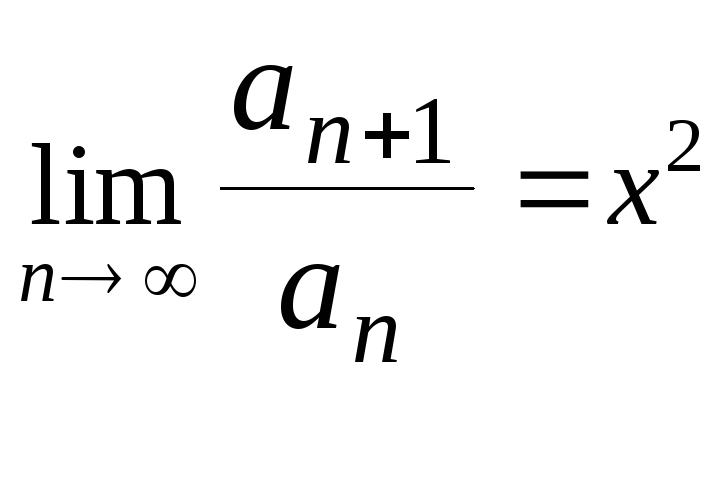Щоб ряд збігався за ознакою Даламбера, беремо- область збіжності рядуза теоремою про абсолютну збіжність.

При ряднабере вигляду. Ясно, що цей ряд збігається абсолютно, таким чином, область збіжності ряду. Усередині цієї області рядможна почленно продиференціювати:

при . Тоді

Остаточно сума ряду при.

2. Знайти суму ряду .

За ознакою Даламбера

. Ряд збігається при.

При рядрозбігається за зауваженням до необхідної ознаки. Таким чином, область збіжності ряду. Усередині цієї області рядможна почленно проінтегрувати.

Продиференціюємо ліву й праву частини останньої рівності

Остаточно сума ряду при.

Лекція 48

174. Допоміжні формули

1. .

Доведення.

.

.

Аналогічно визначаються інтеграли

.

2. при всіх

Доведення

.

.

3. при.

175 Ряди Фур'є для функцій з періодом T = 2l

Означення. Ряд вигляду (1)

, де - дійсні числа, називаєтьсятригонометричним.

Якщо ряд збігається, то його сума – періодична функція з періодом T=2l, тому що періоди функцій ,, а загальний період для всіх,.

Нехай тригонометричний ряд (1) рівномірно збігається до функції на відрізку. Тоді ряд можна почленно проінтегрувати.

1.

.

Таким чином, (*)

2. Визначимо

+або

. (**)

3. Визначимо

або . (***)

Означення. Тригонометричний ряд (1), де коефіцієнти визначаються за формулами,,, називається рядомФур'є.

Висновок. Якщо інтегрована на функція подана рівномірно збіжним тригонометричним рядом, то цей ряд збігається з рядом Фур'є, тобто,,.

176. Формулювання достатньої умови розкладності функції в ряд Фур'є

Означення. Функція називаєтьсякусково-неперервною на , якщо вона неперервна на цьому відрізку, можливо, крім скінченного числа точок усувного розриву або розриву першого роду й,скінченні.

Означення. Кусково-неперервна на функція називаєтьсякусково-гладкою, якщо її похідна кусково-неперервна на .

Теорема Діріхле. Якщо функція є кусково-гладкою на, то складений для неї ряд Фур'є збігається до. Таким чином,

, причому , дляй

.

Зауваження. Якщо в точці С розрив 1-го рода, то , в точках неперервності(пояснити самостійно).

177. Окремі випадки ряду Фур'є

1. , тобто, тоді;

, ,.

2. -парна, тоді,,,, тобто парна функція, якщо має розкладання в ряд Фур'є, то тільки за косинусами.

3. - непарна, тоді,,

,

, тобто непарна функція, якщо має розкладання в ряд Фур'є, то тільки за синусами.

4) Якщо функція задана на, то залежно від типу розкладання (за косинусами, або за синусами) її можна довизначити парним або непарним способом, потім періодично продовжити на всю числову вісь. І цю нову періодичну функцію розкласти в ряд Фур'є. Отриманий ряд Фур'є на інтервалізбігається з даною функцією.

5. Якщо функція задана на, то періодично продовжуємо її на всю числову вісь. Цю нову функцію розкладемо в ряд Фур'є, що назбігається з даною функцією,.

Лекції 49, 50

178. Підсумовування числових рядів за допомогою рядів Фур'є

Лема. Інтеграл від періодичної функції на інтервалі довжиною в один період є величиною сталою.

Доведення.

.

Приклад

. Функція задана на інтервалі .

Періодично довизначимо дану функцію на .,. Нову періодичну функцію подамо у вигляді ряду Фур'є. Функція загального вигляду, тому визначаємо всі коефіцієнти.

де сума отриманого ряду.

Визначимо суму ряду при :

- за теоремою Діріхле.

Зауважимо, що функція при , тобто найчастіше в точці розриву значення суми ряду Фур'є не збігається зі значенням функції.

Визначимо суму ряди при :

, Зауважимо, що , тобто в точці неперервності функції значення суми ряду Фур'є завжди збігається зі значенням функції.

Розглянемо ряд Фур'є для даної функції при :

Звідси одержимо суму числового ряду

або , таким

чином, за допомогою ряду Фур'є можна одержати суми деяких числових рядів.

179. Виведення формули Ейлера

Формула Ейлера: (- будь-яке дійсне число,).

Виведення

Відомо, що при.

Формально подамо функцію у вигляді степеневого ряду

(1)

Розглянемо ряд (2) - знакододатний ряд, застосуємо ознаку Даламбера:

, тобто ряд (2) збігається при . За теоремою про абсолютну збіжність ряд (1) збігається абсолютно прий тоді доданки цього ряду можна згрупувати:

(Доведення теореми про абсолютну збіжність для степеневих рядів у комплексній області розглянуто в ТФКЗ (теорії функцій комплексного змінного)).

180. Комплексна форма запису ряду Фур'є

Аналогічно .

Ряд Фур'є

тут уведені позначення коефіцієнтів: ,,.

Тоді ,

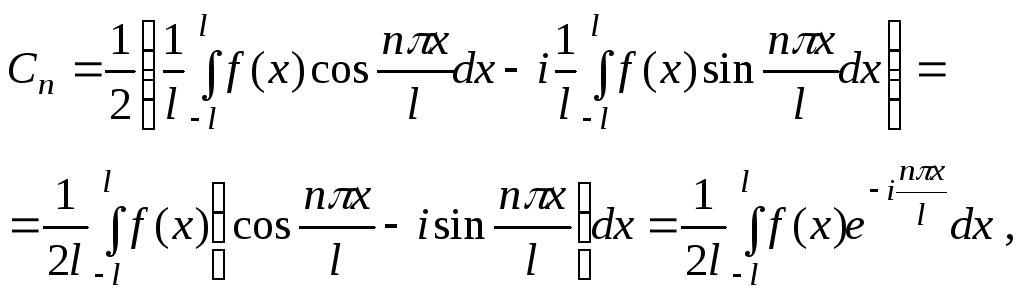аналогічно визначаємо

.

Зауважимо, що йодержано із формули для визначення коефіцієнта.

Остаточно ряд Фур'є набере вигляду , де.

Додаток