Лекція 36

121. Задача про визначення маси неоднорідної оболонки

Нехай гладка поверхня задана рівняннямі вектор нормалі,- замкнена крива, що повністю лежить на поверхній не перетинає її меж.

Означення. Якщо, обходячи будь-яку таку замкнену криву , векторповертається в початкову точку обходу із протилежним напрямком, то поверхнюназвемоодносторонньою. А якщо вектор не змінить свій напрямок, то поверхнюназвемодвосторонньою.

Прикладом односторонньої поверхні є лист Мьобіуса, що виходить із довгої паперової смуги , склеєної по лініїзтаким чином, щоб точказбіглася із точкою, а точка- із точкою.

Надалі будемо розглядати тільки двосторонні поверхні.

Нехай оболонка має форму гладкої поверхні, товщина її стала й набагато менша площі. Густина оболонки. Одиниці виміру густини, тобто щільність за товщиною оболонки не міняється.

Область - проекція поверхніна площину. Розбиваємо поверхнюдовільним чином начастин. Площу кожної частини позначимо через.

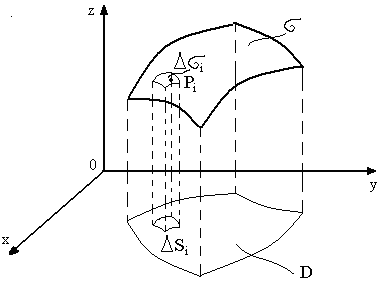
У кожній частині довільним чином вибираємо точку . Оскільки дроблення дрібне, а функціянеперервна, то можна вважати, що густина на ділянцістала й дорівнює. Тоді маса кожної ділянки дроблення дорівнює, а маса всієї оболонки. За ранг дробленняберемо найбільший з діаметрів описаних сфер навколо. Чим ближчедо нуля, тим дрібніше дроблення поверхні.-- а інтегральна сума.

Означення. Якщо існує й дорівнює скінченному числу, то його називають поверхневим інтегралом за площею поверхній позначають

.

Зауваження. Один із фізичних змістів поверхневого інтеграла за площею поверхні - це маса оболонки:

.

Якщо , то- площа поверхні.

122. Формулювання теореми про існування поверхневого інтеграла за площею поверхні

Теорема. Якщо - гладка поверхня, а функція, то інтеграліснує, тобто границя n-ої інтегральної суми дорівнює скінченному числу й не залежить від способу дроблення поверхній вибору точок(без доведення).

123. Дві основні властивості поверхневого інтеграла за площею поверхні

1. , тобто поверхневий інтеграл за площею поверхніне залежить від вибору сторони поверхні. Тут- верхня сторона поверхні,- нижня.

2. Якщо і без спільних внутрішніх точок, то

.

Доведення обох властивостей випливають із визначення поверхневого інтеграла. У властивості 2 загальну частину границь областей ,беремо за одну з ліній дроблення поверхні.

124. Обчислення поверхневого інтеграла за площею поверхні

Спроектуємо все на площину. Якщонезамкнена й гладка поверхня, то областьбуде розбита начастин проекціями. Оскількимале йнеперервна, то можна вважати, щоплоска. Для простоти на кресленніпрямокутник.

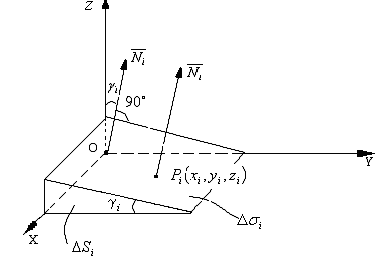
Ясно, що ,, тодій.

,

,

=.

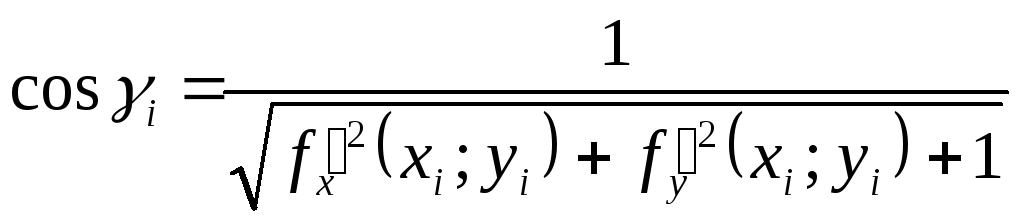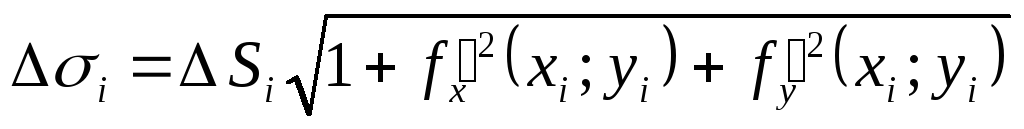
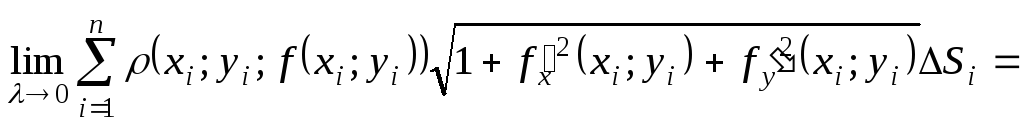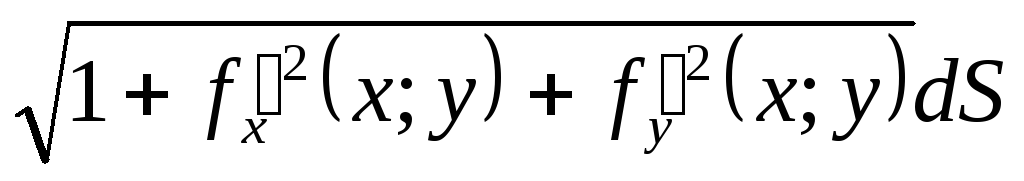Приклад

Обчислити , де- частина поверхні, вирізана поверхнею.

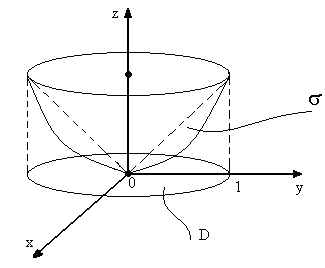
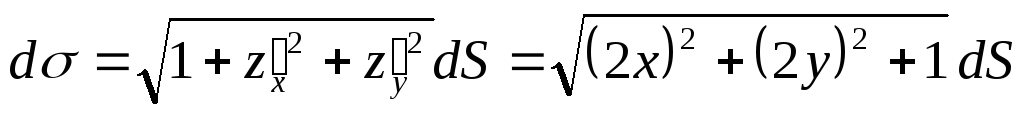
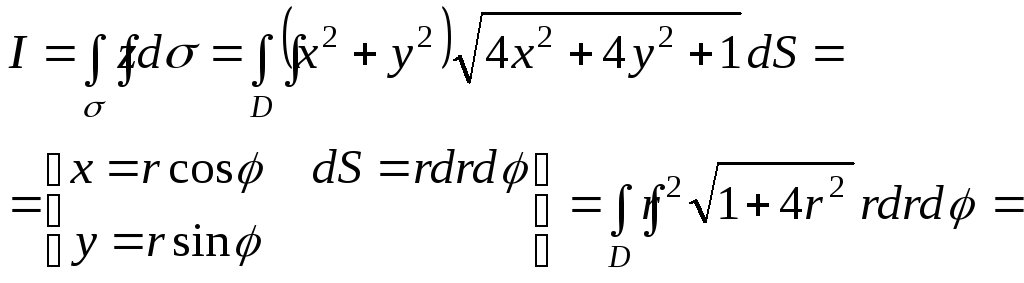
Лекція 37

125. Задача про обчислення потоку рідини через поверхню

Розглянемо сталий потік рідини, тобто - не залежить від часу.

.

З фізики відомо, що потік - це кількість рідини, що протікає через дану поверхню за одиницю часу.

Нехай - гладка двостороння поверхня, задана рівнянням, довільним чином розбита начастин.

- одиничний вектор нормалі до нескінченно малого елемента поверхні . Нормаль характеризує сторону поверхні. (.)- довільно взята точка на.- густина потоку рідини,.

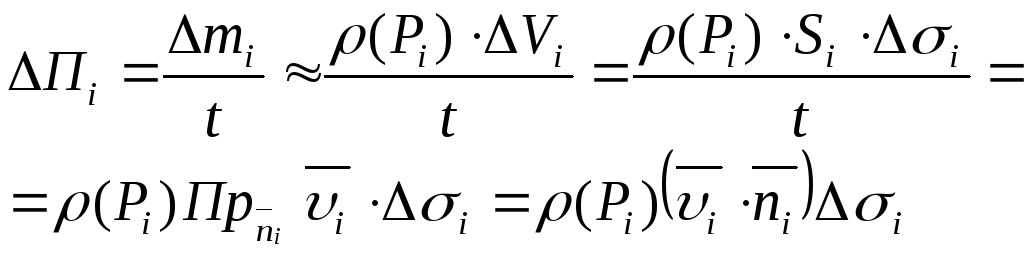
EMBED PBrush

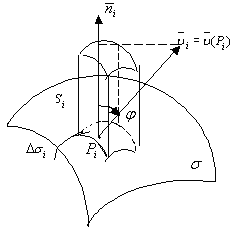
Тут - висота об'єму, а- площа основи;.

Ясно, що потік рідини через поверхню :

, або , де- ранг дроблення (див. п. 121).

Означення. Якщо остання границя існує й дорівнює скінченному числу, то це число називається поверхневим інтегралом за координатами і позначається:

. . . . (*).

Оскільки - одиничний вектор, то його координати визначаються через напрямні косинуси:.

. У пункті 124 введена проекція на площину:, або.

Аналогічно визначаються проекції на площини,:,.

Знак вибирається за «правилом косинусів», тобто якщо ,,- гострі, тобто їхні косинуси додатні, то вибираємо знак плюс, якщо,,- тупі, то вибираємо знак мінус, тому що,,- площі відповідних проекцій.Таким чином,

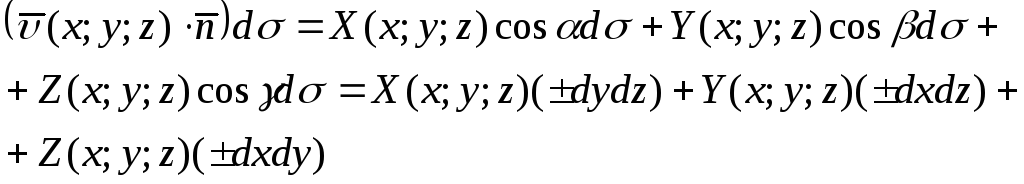
і остаточно

.

Зауваження. Теорема існування поверхневого інтеграла за координатами дається аналогічно теоремі існування поверхневого інтеграла за площею поверхні в п. 122.

126. Дві основні властивості поверхневого інтеграла за координатами

1. .

Тобто поверхневий інтеграл за координатами залежить від сторони поверхні , тому що нормалікідоспрямовані в протилежні сторони.

2. Якщо йбез спільних внутрішніх точок, то

.

Тут при доведенні спільна межа областей ібереться за одну з ліній дроблення області. Аналогічно доводиться властивість 2 для нижньої сторони поверхні.