107. Вектор-функція скалярного аргументу і її границя

Означення. Якщо відповідає певний вектор , то кажуть, що на множині T визначений вектор-функція скалярного аргументу

.

Означення. Лінія L, описувана кінцем радіуса-вектора , називається годографом вектор-функції.

EMBED PBrush

Зауваження. Якщо t – час, то годограф – це траєкторія руху точки .

Означення. Якщо таке, що прий, тоназивається границею вектор-функції при, тобто.

Наслідок. , тоді

. Оскільки

то, аналогічно,.

Отже, для того, щоб , необхідно й достатньо, щоб,,.

Означення. Вектор-функція називається неперервною в точці , якщо, тобто, або.

108. Похідна вектор-функції

Означення. Якщо існує границя , то вона називається похідною вектор-функції й позначається.

Наслідок. Оскільки , то з існуванняіснування границь,,і навпаки.

Таким чином для того, щоб мала похідну, необхідно й достатньо, щоб,,були диференційовані.

Лекція 33

109. Геометричний зміст похідної вектор-функції

При й хордарозвертається до положення дотичної:.

Геометричний зміст похідної вектор-функції: лежить на дотичній, проведеній до годографа, і напрямлена у бік зростання параметра.

Зауваження. Годограф можна розглядати як графік функції, заданої параметрично:

~.

Означення. називається особливою, якщоабо не існує.

Означення. Крива називається гладкою, якщонеперервно диференційована функція без особливих точок.

Теорема. Довжина нескінченно малої дуги гладкої кривої еквівалентна стягуючій її хорді, тобто

(без доведення).

Зауваження.Перша важлива границя є окремим випадком цієї теореми, тому що

.

EMBED PBrush

110. Дотична й нормальна площини до кривої в просторі

Нехай - гладка крива. Оскільки векторлежить на дотичній, то він є напрямним вектором цієї прямої.- точка дотику.

Рівняння дотичної: .

У той же час вектор перпендикулярний до нормальної площини, тобто

й рівняння нормальної площини:

.

111. Механічний зміст похідної вектор-функції

Нехай матеріальна точка рухається по годографу вектор-функції.

EMBED PBrush

Уведемо в розгляд початок відліку точку О і дугову координату S, що спрямована у напрямку руху . Тодій. Оскільки, тут- вектор-хорда,- довжина дуги, то за теоремою пункту 109, векторлежить на дотичній, тобто- одиничний вектор дотичної, що спрямований у напрямку руху точки, а. Отже,.

Механічним змістом похідної вектор-функції за часом є вектор швидкості матеріальної точкипід час руху по кривій.

112. Задача про визначення маси неоднорідної матеріальної лінії

Нехай матеріальна лінія є гладкою кривою , що задається вектор-функцією. Погонна густина цієї лінії. Розмірність густини, де- розмірністи маси й довжини лінії.

Довільним чином ділимо криву начастин і на кожній дузівибираємо точку. Вважаємо густину на дузірівною, тоді маса дуги, де- довжина дуги.

Маса всієї матеріальної лінії

(*).

І чим дрібніше розбиття, тим точніша ця рівність.

Найбільшу з довжин дуг позначимо буквоюй назвемо рангом розбиття. Якщо, то дугистягуються в точки, а. Сума (*) залежить від способу розбиття лініїй вибору точок.

Визначимо , якщо він існує, то його називають криволінійним інтегралом по довжині дуги й позначають.

Фізичний зміст криволінійного інтеграла по довжині дуги - маса матеріальної лінії

.

113. Задача про роботу змінної сили під час руху точки по кривій

Нехай точка рухається уздовж кривої, що є годографом вектор-функції. До точки прикладена сила

.

Визначити роботу сили при переміщеннізв,- гладка, а. Довільним чином розбиваємо кривуначастин і на кожній дузівибираємо точку. Оскільки дугадосить мала, анеперервна, то можна вважати, що на цій ділянці сила стала й. І тоді робота силина ділянці:.

А робота на всій кривій :, і чим дрібніше розбиття, тим точніша ця формула. Найбільшу з довжин дугпозначимо буквою, що називають рангом розбиття. Якщо, то(але не навпаки). Сумазалежить від способу розбиття кривоїй вибору точок. Розглянемо(*).

Означення. Якщо границя (*) існує, то вона називається криволінійним інтегралом за координатами і позначається .

Криву називають контуром інтегрування.

Таким чином, робота змінної сили під час руху точки по кривійдорівнює криволінійному інтегралу

.

Лекція 34

114. Формула зв'язку криволінійних інтегралів за координатами і довжиною дуги

Нехай L - гладка крива, задана вектор-функцією

Розглянемо одиничний дотичний вектор

, вектор

Запишемо теорему пункту 109 через диференціали:

.

Криволінійний інтеграл за координатами

тут .

Таким чином, криволінійний інтеграл за координатами існує, якщо існує криволінійний інтеграл за довжиною дугий навпаки.

115. Формулювання теореми існування криволінійного інтеграла

Теорема. Якщо - гладкакрива, а вектор-функція

, то існує криволінійний інтеграл за координатами , тобто існує границя n-ї інтегральної суми(пункт 113), що не залежить від способу розбиття кривої L і вибору точок.

Зауваження. Оскільки L - гладка, а F(M), тотеж неперервна на L.

Доведення

а оскільки крива L гладка, то неперервно диференційовані й без особливих точок, тобто, аналогічно- неперервні на L функції.

Отже, .

Із зауваження й формули зв'язку випливає, що якщо й L - гладка, то криволінійний інтеграл за довжиною дуги теж існує.

116. Дві основні властивості криволінійних інтегралів

1. Криволінійний інтеграл за довжиною дуги AB не залежить від вибору напрямку інтегрування, тобто

.

Доведення

За означенням

,

- довжина дуги не залежить від напрямку її виміру.

2. Криволінійний інтеграл за координатами залежить від вибору напрямку інтегрування, тобто

Доведення

За визначенням

EMBED PBrush

, що й потрібно було довести.

Зауваження.Якщо контур АВ замкнений, то криволінійний інтеграл записують так:

.

117 . Обчислення криволінійних інтегралів

Почнемо із криволінійного інтеграла за координатами:

Обчислимо .

Крива АВ задана рівняннями ,.

За теоремою Лагранжа , дележить міжі;

, тому що x=x(t) - неперервна.

Оскільки інтеграл не залежить від вибору точок (пункт115), то нехай, тоді,

тобто криволінійний інтеграл зводиться до визначеного.

Остаточно: .

Аналогічно: .

.

З пункту 114 випливає, що метод обчислення криволінійного інтеграла за довжиною дуги такий самий, що й метод обчислення криволінійного інтеграла за координатами.

Оскільки то

Приклади.

1. Визначити роботу сили.

Уведемо параметризацію кривої L

2. Визначити роботу сили під час руху точки М по прямій від точки А(1,0,4) до точки В(7,4,2).

3. Визначити масу параболи , якщо- густина.

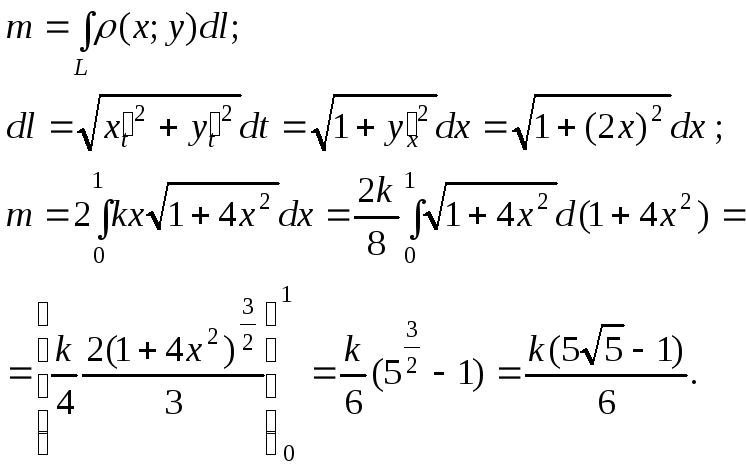
Лекція 35

118. Формула Гріна

Теорема. областьправильна уздовж осій, функції,,,, тоді, де- замкнений контур (границя областіD)з обходом проти ходу годинникової стрілки.

Доведення.

де - замкнений контурзобходом протигодинниковоїстрілки.

Аналогічно , тоді.

119. Умови незалежності криволінійного інтеграла від шляху інтегрування

Означення. Якщо , то кажуть, що криволінійний інтеграл не залежить від шляху інтегрування.

, ,,, де- правильна область уздовж осей,.

Чотири рівносильні умови:

1. Інтеграл , узятий за будь-яким замкненим контуром, дорівнює нулю.

2. Інтеграл не залежить від шляху інтегрування.

3. Вираз є повним диференціалом деякої функції, визначеної в області.

4. В області :.

Доведення проводимо за схемою .

1. Оскільки ,- будь-який замкнений контур в області.

, тобто інтеграл не залежить від шляху інтегрування .

2. Позначимо

тому що .

Таким чином, , аналогічно доводиться, що. Отже,. ()

Визначимо цю функцію:

3. Оскільки ,, топри

4. Для будь-якого замкненого контура L, що повністю лежить в D,

, тому що в D..

Таким чином, усі чотири умови рівносильні.

120. Механічні застосування криволінійного інтеграла за довжиною дуги (список формул)

густина матеріальної лінії L

1. Моменти інерції матеріальної лінії:

2. Статичні моменти матеріальної лінії:

3. Координати центра мас матеріальної лінії

117