98. Найбільше й найменше значення функції в замкненій області

Схема визначення в

1. Для функції визначаємо точки, підозрілі на екстремум із системи.

2. Визначаємо значення функції в тих точках, які належать області .

3. Оскільки функція на границі є функцією однієї змінної: 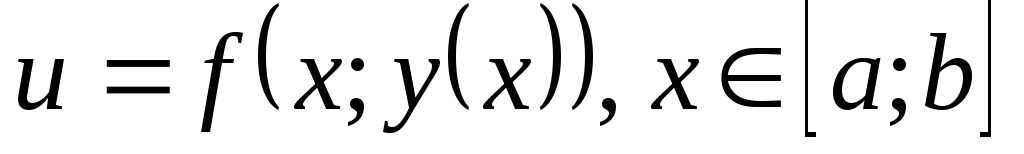, то найбільше й найменше значення цієї функції знаходяться на кінцях відрізка або у внутрішніх точках, підозрілих на екстремум. Визначаємо значення функції в цих точках і на кінцях відрізка (для дослідження на границі можна використовувати пункт 97).

4. Із всіх отриманих значень функції вибираємо найбільше й найменше.

Приклад

; Область обмежена лініями.

1. .

Точка підозріла на екстремум і.

.

1. Границя області розпадається на три частини.

~.

,

, ,

.

Точка , що лежить на границі, підозріла на екстремум.

,

~ ,,.

Точка , що лежить на границі, підозріла на екстремум.

,

,,

~ ,.

Цю точку ми вже досліджували, вивчаючи границю .

2. Вибираємо найменше й найбільше значення:

.

99. Задача про об'єм криволінійного циліндра

.

Криволінійний циліндр – це тіло, що обмежене циліндричною поверхнею (напрямна – крива , твірні паралельні осі), площиноюй поверхнею.

.

Для визначення об'єму криволінійного циліндра розіб`ємо область довільним чином начастин.

На кожній ділянці довільним чином вибираємо точки й обчислюємо.

Позначимо площу кожної ділянки через . Побудуємо прямі циліндри з нижньою основоюй висотою. Ясно, що об'єм криволінійного циліндра наближено дорівнює сумі об'ємів таких “волокон” – прямих циліндрів:.

Суму називають-ю інтегральною й вона залежить від способу розбиття області й вибору точок , і чим дрібніше розбиття, тим точніша рівність. Навколо кожногоопишемо коло з діаметром.називається рангом розбиття. Якщо , той усістягуються в точки.

Означення. Якщо границя послідовності –х інтегральних сум при існує, то вона називається подвійним інтегралом від функції по областій позначається.

Лекція 30

100. Задача про визначення маси неоднорідного тіла

Нехай густина у кожній точці обмеженої області V описується неперервною й додатно визначеною функцією .

Розіб'ємо область V довільним чином на n частин і в кожній частині довільно виберемо (·) . Позначимо об`єм кожної частини через. Обчислимо густину. Оскільки, а об’ємдуже малий, то можна вважати, що густина для цієї частини й дорівнює, тоді маса цього нескінченно малого елемента, а маса всієї області

(**),

n-а інтегральна сума (**) залежить від способу розбиття області V і вибору точок , чим дрібніше розбиття, тим точніша рівність (**). Навколо кожної частиниопишемо сферу з діаметром. Ранг розбиття, й чим дрібніше розбиття, тим ближчедо нуля.

.

Означення. Якщо границя послідовності n-х інтегральних сум (**) при існує, то він називається потрійним інтегралом від функціїпо області V і позначається.

Зауваження. Аналогічно можна визначити кратний інтеграл в n-мірному просторі, де точки має n координат,- обмежена область n-вимірного простору, функція:

,

тут - міра нескінченно малого елемента (н.м. елемента) довільного розбиття області,- довільна точка цього н.м. елемента,- ранг розбиття.