Лекція 21

Застосування визначеного інтеграла до задач геометрії

68. Визначення площі плоскої області

1. Якщо y = f(x)  C[a;b] і f(x)0, то (див. пункт 63)

.

2. Якщо y = f(x)  C[a;b], але змінює знак, то площа заштрихованої області визначається за формулою

.

3. Якщо область D обмежена лініями ,,,, то

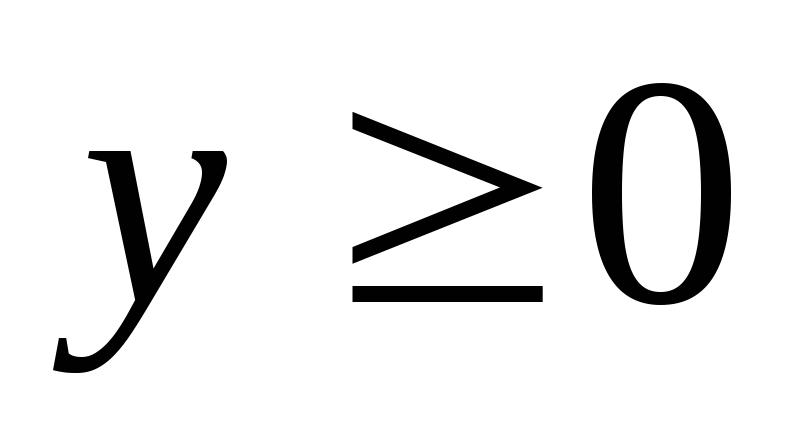
4. Якщо в криволінійній трапеції крива АВ задається параметрично ,,, то

.

69. Площа криволінійного сектора

Розглянемо полярну систему координат:

Якщо вся додатна частина осі х декартової системи координат збігається з полярною піввіссю Ох, початок відліку – з полюсом О, а вісь у буде перпендикулярна до осі х, то формули переходу з полярної в декартову систему координат матимуть вигляд: ,. Крива в полярній системі координат задається рівнянням. Наприклад, рівняння кола із центром у точці О і радіусом 2 у декартовій системі координат, у полярній системі r=2,. А коло із центром у точцій радіусом 2 у декартовій системі координатабо, у полярній системі ,.

Розглянемо криволінійний сектор, обмежений лініями ,,.

Для визначення площі криволінійного сектора розіб'ємо відрізок довільним чином на n частині в кожному інтервалі довільно виберемо кут. Обчислимо значення функції.

Позначимо площу нескінченно малого криволінійного сектора за . Тоді, а- n-а інтегральна сума для функції. Уведемо ранг розбиття , що характеризує дрібність розбиття, причому при,.

Якщо , то за теоремою 2 пункту 62 маємо:

, тобто

.

70. Об'єм тіла обертання

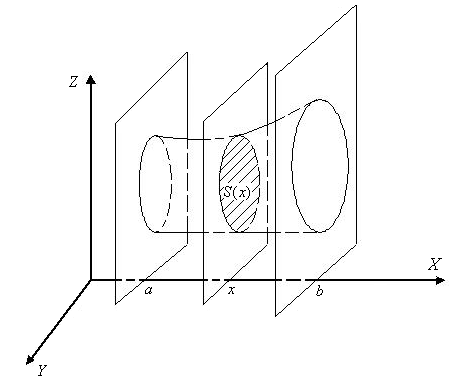
для тіла V відома площа будь-якого перпендикулярного до осі OX перерізу S(x)  C[a;b]. Визначимо об'єм такого тіла. Розіб'ємо відрізок [a;b] довільним чином на n частин: . Через ці точки проведемо площини, перпендикулярні до осіOX. На кожному інтервалі вибираємо точкуй обчислюємо площу перерізу. Об'ємміж площинами,визначимо за формулою, а весь об'ємі чим дрібніше розбиття, тим точніше остання формула. Ранг розбиття, якщо, то(але не навпаки). Ясно, щоза теоремою 2 пункт 62. Отже,.

Розглянемо тіло обертання навколо осі OX.

Обертаючи криву y = f(x)  C[a;b] навколо осі OX, одержимо тіло обертання.

Оскільки , тоді

.

Лекція 22

71. Довжина дуги кривої

Нехай крива задана на відрізкурівнянням.

Означення. Крива на відрізку називається гладкою, якщо. Визначимо довжину дуги гладкої кривої.

Довільним чином розбиваємо відрізок наn частин: (на рисунку). На дузі кривоїданому розбиттю відповідають точки, де.

Довжина хорди

За теоремою Лагранжа , де.

Тоді (1).

Довжина вписаної ламаної

.

Щоб визначити довжину дуги кривої , переходимо до границі, коли довжина найбільшої хорди прямує до нуля.

З формули (1) випливає, що якщо , то.

Позначимо найб.- ранг розбиття.

Таким чином, , а оскільки функція, то за теоремою 2 пункту 62 границяn-ї інтегральної суми не залежить від способу розбиття відрізка , вибору точокі дорівнює скінченному числу, тобто

.

72. Довжина дуги, якщо крива задана параметрично

Якщо плоска крива задана параметрично:,,,іпри, то в інтеграліможна зробити заміну змінноїі:

(*)

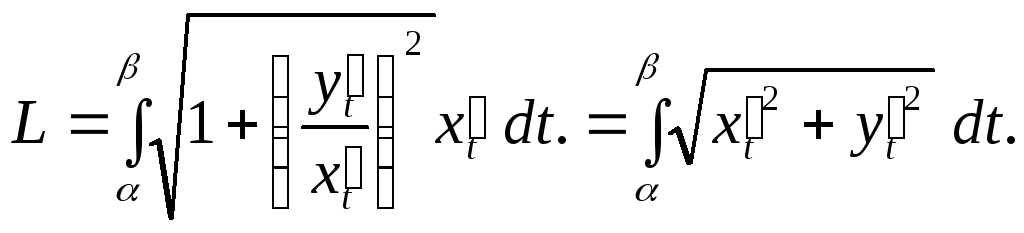Зауваження. Якщо крива лежить у просторі, тобто,і, то можна довести, що довжина дуги кривої визначається за формулою

Тут підінтегральний вираз

називають диференціалом довжини дуги.

73. Площа поверхні обертання

Нехай гладка крива лежить у площиніі задана рівнянням,. Тоді площа поверхні обертання кривоїнавколо осі Ох визначається за формулою

(**)

Доведення.

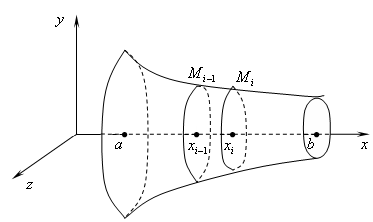
Розіб'ємо відрізок довільним чином наn частин Площинирозбивають поверхню обертання наn частин, площа бічної поверхні кожної частини як площа бічної поверхні зрізаного конуса дорівнює

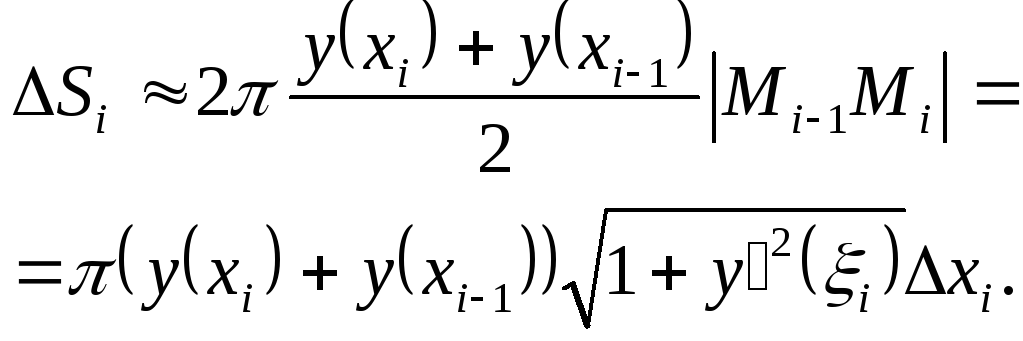
Площа всієї поверхні обертання

,

,

оскільки ,ілежить між.

Таким чином, і чим дрібніше розбиття, тим точніша остання формула. Введемо ранг розбиттяі

.

Повторюючи аналогічні розмірковування з п.71, дійдемо формули

.

Зауваження. Якщо гладка крива задана параметрично, тобто,,

, іпри, то

.

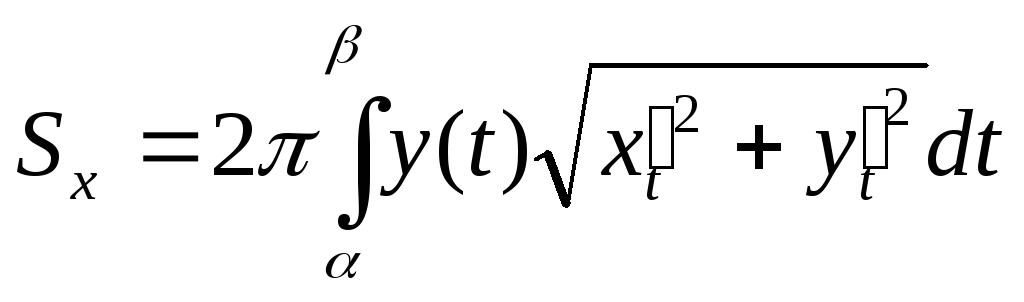74. Довжина дуги кривої у полярній системі координат

крива задана рівнянням,. Тоді за параметрвізьмемой формуланабере вигляду

Доведення

Оскільки , то,

Лекція 23

Застосування визначеного інтеграла до задач фізики

75. Маса дуги кривої

Проаналізуємо отримані формули при розв`язанні геометричних задач:

,	,
,	,
,	,
,	,
,	.

Отже, підінтегральні вирази - це диференціали, складені для відповідного нескінченно малого елемента. Тому, щоб уникнути більших викладень, розглянемо на задачах з фізики новий метод.

Нехай у просторі задана крива

У кожній точці кривої задана погонна густина Маса нескінченно малого елемента, тоді.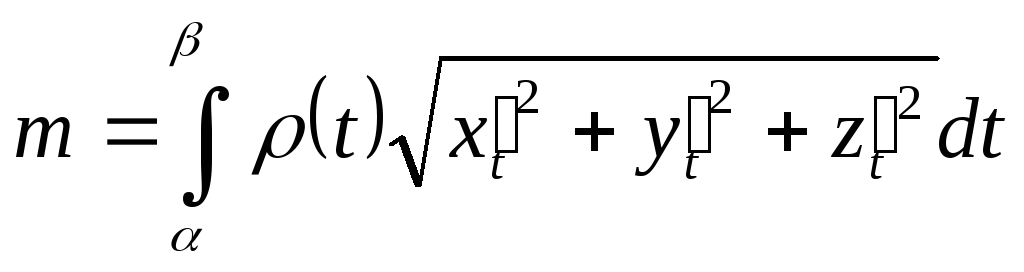

76. Статичний момент дуги кривої. Координати центра мас

З фізики відомо, що статичний момент матеріальної точки масищодо деякої осі дорівнює, де- відстань від точки до осі.

Нехай у площині задана крива , де- погонна щільність. Для н.м. елемента дуги кривої статичний момент щодо осіОХ: , а статичний момент всієї кривої. Аналогічно визначається статичний момент щодо осі ОУ:.

Центр мас точка має таку властивість, що якщо в цій точці зосередити всю масу кривої, то статичний момент цієї маси щодо осізбігається зі статичним моментом кривоїщодо осі(тобто з моментом маси розподіленої по цій кривій).

Таким чином, або.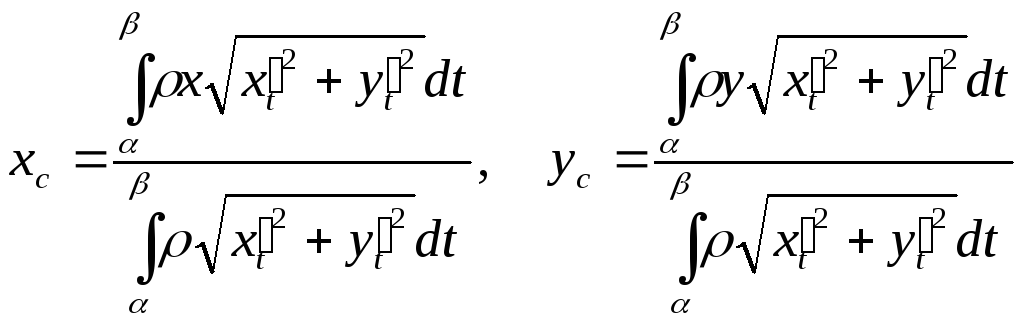

Самостійно одержати координати центра мас, якщо крива задана в декартовій або в полярній системі координат.

77. Момент інерції дуги кривої

Момент інерції матеріальної точки масищодо деякої осі дорівнює, де- відстань від точки до відповідної осі.

Нехай у площині задана крива як у пункті 76. Тоді момент інерції н.м. елемента дуги кривої щодо осіОХ: , а для всієї кривоїL: .

Аналогічно визначається момент інерції щодо осі OY: .

Полярний момент інерції розглядається щодо полюса O: .

Самостійно записати всі ці моменти в декартовій або в полярній системі координат.

78 Робота змінної сили

Нехай точка рухається уздовж осіпід дією сили, що лежить на осі.

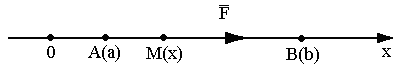
Коли точка пройде н.м. елемент шляху, силазробить роботу. Робота змінної силина відрізкувизначається за формулою.

79. Робота з подолання сили тяжіння

Розглянемо це питання на прикладі про обчислення роботи, яку потрібно зробити, щоб викачати воду з вертикальної циліндричної діжки, що має радіус основи й висоту.

Щоб підняти н.м. шар води завтовшки до краю діжки, потрібно зробити роботу:

Тоді робота з викачування всієї води з діжки

.

Лекція 24

80. Сила тиску на плоску пластину

Нехай круглу пластину радіуса R опустили вертикально у воду так, що її центр перебуває на глибині H під водою. Визначити силу тиску води на цю пластину.

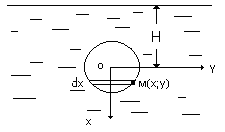
Складемо диференціал сили тиску води на н.м. елемент пластини:

, - питома вага води,h- відстань від поверхні води до н.м. елемента пластини.

.
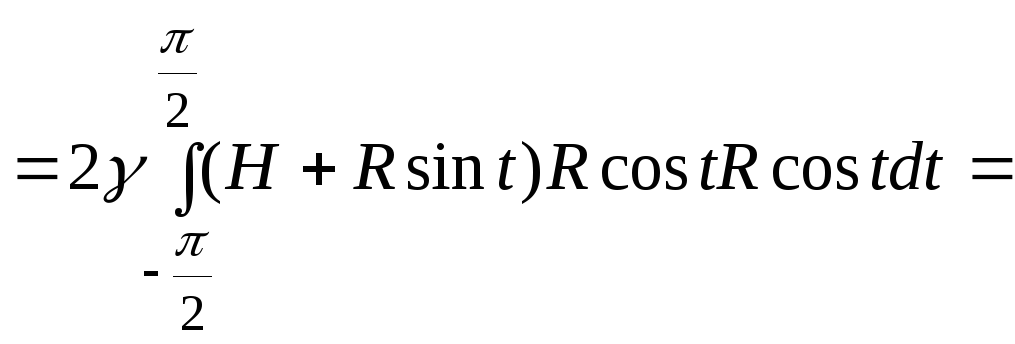
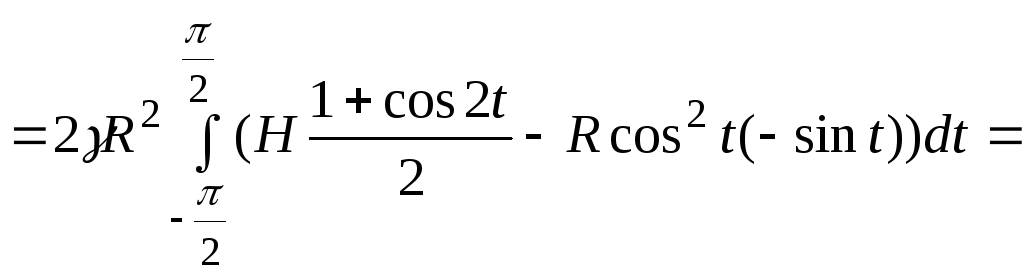
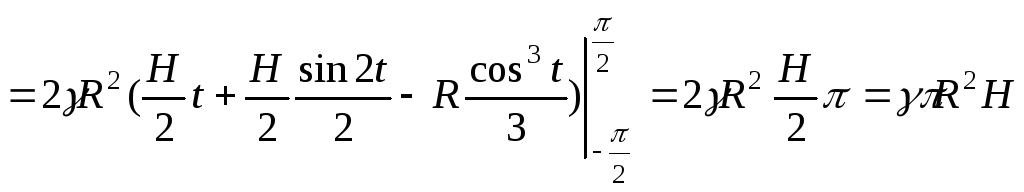