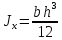8. Выбор предельного напряжения и нормативного коэффициента запаса прочности.

Выбор предельного напряжения

1. Пластичные материалы

Отказ элемента конструкции связан с появлением больших пластических деформаций, достигаемых при пределе текучести

,

.

2. Хрупкие материалы

Хрупкие материалы не образуют площадки текучести. Отказ элементов конструкции связан с наступлением разрушения, предельными напряжениями являются пределы прочности при растяжении или сжатии

,

.

Выбор нормативного коэффициента запаса прочности

Факторы, влияющие на выбор:

1. неоднородность материала (трещины); чем больше неоднородность, тем больше ;

2. изменчивость нагрузки (природные воздействия), чем больше изменчивость нагрузки, тем больше ;

3. условия работы конструкции (степень ответственности, срок службы), чем выше ответственность и срок службы конструкции, тем больше ;

4. недостатки расчетных схем (идеализация), чем точнее расчетная схема, тем меньше .

9. Три основные задачи при расчетах на прочность (жесткость).

Три основные задачи ДПМ:

• Проверка прочности

Условие прочности:

,

– допускаемое напряжение,

,

– предельное (опасное) напряжение, вызывающее отказ элемента конструкции.

– нормативный коэффициент запаса прочности.

Поверочный расчет:

,

– фактический коэффициент запаса прочности.

• Подбор сечения

.

• Определение допускаемой нагрузки

.

Условие жесткости:

.

10. Статически неопределимые системы при растяжении (сжатии), особенности.

Статически неопределимая система – система, в которой реакции связей не могут быть определены с помощью одних уравнений статики.

Степень статической неопределимости – число лишних связей.

Чтобы раскрыть статическую неопределимость к уравнениям статики нужно добавить уравнения совместности деформаций.

Особенности

1. Величина усилий зависит от распределения жесткостей.

2. Температурные воздействия приводят к возникновению усилий.

3. Неточности изготовления элементов при сборке ведут к появлению монтажных усилий и напряжений.

11. Определение температурных усилий в статически неопределимых стержневых системах.

Температурные усилия – возникающие за счет изменения температуры системы.

,

– температурный коэффициент линейного расширения материала,

,

.

При охлаждении продольная сила будет растягивающей, при нагревании – сжимающей.

12. Монтажные усилия и напряжения, возникающие в статически неопределимых системах после их сборки.

Монтажные усилия (напряжения) – усилия (напряжения), возникающие при сборке системы в результате неточного изготовления ее элементов.

Пример

Средний стержень короче на .

Приложив монтажные усилия , , , все три стержня соединяются в узле . Средний стержень будет растянут, боковые сжаты.

,

.

13. Геометрические характеристики поперечных сечений стержней. Центральные оси, главные центральные оси сечений. Вычисление моментов инерций простейших и составных частей.

Геометрические характеристики поперечных сечений стержней

1. Площадь поперечного сечения

.

2. Статические моменты

Статический момент сечения относительно оси – сумма произведений элементарных площадок на их расстояния до этой оси

,

,

,

,

,

.

Центральные оси – оси, проходящие через центр тяжести сечения (, ). Частный случай центральных осей – оси симметрии.

3. Моменты инерции

Момент инерции сечения относительно оси – сумма произведений элементарных площадок на квадрат их расстояний до этой оси

,

,

,

.

Полярный момент инерции сечения относительно точки – сумма произведений элементарных площадок на квадрат их расстояний до этой точки

.

Центробежный момент инерции сечения относительно осей , – сумма произведений элементарных площадок на их расстояния до осей

.

Главные оси инерции – две взаимно перпендикулярные оси, относительно которых . Осевые моменты инерции , – главные моменты инерции.

Главные центральные оси – главные оси инерции, проходящие через центр тяжести сечения (ось симметрии и любая ось, перпендикулярная ей).

Моменты инерции простых сечений

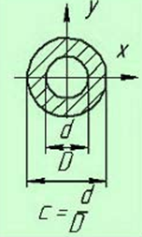
Прямоугольник	Круг	Кольцо

Моменты инерций стандартных прокатных профилей приведены в таблицах.

Двутавр	Швеллер	Уголок равнобокий	Уголок неравнобокий

Момент инерции сечения сложной формы относительно оси равен сумме моментов инерций его составных частей относительно этой оси

.