2.2. Случайные величины и случайные функции

Случайное воздействие в зависимости от характера его проявления с математической точки зрения может быть представлено либо случайной величиной, либо случайной функцией. Понятие случайной функции является более общим, чем случайная величина, так как в нем учитывается фактор времени. Образно говоря, случайная величина характеризует как бы «статику» случайного явления, а случайная функция – динамику. Или другими словами, случайная функция есть случайная величина, проявляющаяся во времени. Изучением случайных величин и функций занимается специальная математическая дисциплина – теория вероятностей. Ниже излагаются некоторые ее положения, необходимые для понимания последующего материала.

2.3. Случайная величина и ее характеристики

Случайная величина – это величина, значение которой является непредсказуемым в ограниченном диапазоне исходных факторов рассматриваемого явления. Наиболее полной характеристикой случайной величины х является ее закон распределения – интегральный F(x) и дифференциальный p(x).

Интегральным законом распределения случайной величины х называется функция F(x), описывающая вероятность Р появления случайной величины x, меньшей некоторого текущего значения переменной х, т. е.

F(x) = P (x  х).

Из определения F(x) следует, что она является неубывающей функцией х для –  х  . Причем F(–) = 0 и F() = 1. Пример вида функции F(х) приведен на рис. 2.1, г.

Дифференциальным законом распределения или плотностью вероятности р(х) называется функция

при этом подразумевается, что функция F(х) непрерывна и дифференцируема.

Из определения функции р(х) следует, что:

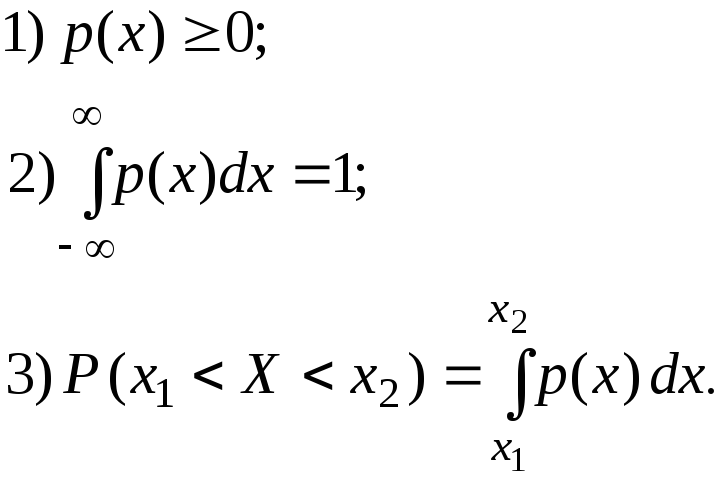
Для дискретной случайной величины плотность вероятности вырождается в распределение вероятностей р(х_i), которое задается конечным рядом. В этом случае очевидно, что интегральный закон распределения случайной величины F(x) может быть выражен через распределение вероятностей Р(х_i) следующим образом:

х_i < х.

Если случайное событие характеризуется несколькими коор-динатами, т. е. может быть представлено как случайный вектор, то это событие рассматривается как многомерная случайная величина. Понятия интегрального и дифференциального законов распределения по аналогии вводятся и для многомерных случайных величин. В этом случае соответствующие функции будут многомерными и в отличие от одномерных случайных величин будут представляться не кривыми, а некоторыми гиперповерхностями в соответствующей системе координат.

Для удобства решения практических задач реальные законы распределения случайных величин «округляют» с той или иной степенью точности до известных типовых законов, свойства и параметры которых изучены и определены.

В инженерной практике, исходя из удобства использования, наибольшее распространение для характеристики случайных величин получил дифференциальный закон распределения. Один из примеров вида дифференциального закона распределения приведен на рис. 2.1, в. Однако для решения ряда практических задач нахождение закона распределения и его дальнейшее использование требуют значительных трудозатрат и большого объема вычислительной работы. Иногда оказывается удобнее воспользоваться набором числовых параметров, характеризующих различные свойства случайной величины. Этот набор важнейших параметров состоит из ограниченного ряда начальных и центральных моментов [3].

Начальные моменты k-го порядка случайной величины х определяются из выражений:

– для дискретной случайной величины

, (2.1)

где Р_i – вероятность появления случайной величины х_i;

– для непрерывной случайной величины

(2.2)

Для решения практических задач наиболее важным является первый начальный момент , получивший специальное название – математическое ожидание случайной величины. Математическое ожидание является своеобразным «центром тяжести», вокруг которого происходит «рассеяние» случайной величины.

Центральные моменты k-го порядка случайной величины х определяются из выражений:

– для дискретной случайной величины

(2.3)

– для непрерывной случайной величины

(2.4)

Для практических целей наиболее важными являются второй, третий и четвертый центральные моменты.

Второй центральный момент ₂(Х) = D_x получил специальное название – дисперсия. Дисперсия характеризует степень «рассеяния» случайной величины относительно математического ожидания. Чем больше дисперсия, тем больше разброс случайной величины, и наоборот. Для детерминированной величины с дисперсия равна нулю, т. е. D_c = 0. Для большей наглядности степени разброса случайной величины используют специальный параметр _х

(2.5)

называемый средним квадратическим отклонением случайной величины. Величина _х имеет размерность случайной величины и характеризует ее «средний радиус» рассеяния.

Третий центральный момент ₃ характеризует асимметрию или скошенность плотности распределения. Для количественной характеристики асимметрии используют безразмерную величину, называемую коэффициентом асимметрии S_k ,

. (2.6)

Очевидно, что для симметричной (относительно m_x) кривой плотности распределения случайной величины S_k = 0. Пример положительной асимметрии (S_k  0) плотности распределения приведен на рис. 2.1, в.

Четвертый центральный момент ₄ характеризует степень «ост-ровершинности» распределения. Для количественной характеристики этого свойства используют специальную безразмерную величину, называемую эксцессом Е_х,

(2.7)

В качестве «отправной точки» для оценки «островершинности» распределения используется нормальный закон распределения, для которого . Отсюда значение Е_х для нормального закона распределения согласно выражению (2.7) равно нулю. Таким образом, более «островершинные» кривые по сравнению с нормальным распределением имеют положительный эксцесс и наоборот.

Рассмотренный набор числовых параметров m_x, _x, S_k, E_x довольно полно, но не исчерпывающе, характеризует свойства случайной величины. При необходимости могут быть использованы и другие параметры, например мода, медиана. Однако они получили меньшее распространение.