Коэффициенты статистической линеаризации типовых нелинейных позиционных звеньев

№ пп	Наименование звена и его статическая характеристика	Уравнение звена у = F(х)	Выражения для вычисления коэффициентов статистической линеаризации
			kc0	kc1	kc1
1	Двухпозиционное реле	y = Bsignx
2	y Трехпозиционное реле	B; x > b y = 0;x b –B; x < –b

Продолжение табл. 3.1

№ пп	Наименование звена и его статическая характеристика	Уравнение звена у = F(х)	Выражения для вычисления коэффициентов статистической линеаризации
			kc0	kc1	kc1
3	x Звено с насыщением	Kx;x b y = B; x  b –B; x  –b К =
4	Двухпозиционное реле с зоной нечувствительности	B; x  b x   –B; x  b y = B; x  –b x   –B; x  –b

(3.35)

(3.36)

где Ф₀(р) – передаточная функция замкнутой системы для неслучайной (детерминированной) составляющей воздействия; Ф₁(р) – передаточная функция замкнутой системы для центрированной случайной составляющей воздействия; W_fz(p) – передаточная функция участка системы «воздействие f – выходная величина z»; W(p) – передаточная функция линейной части системы W(p) = W₀(p) W₁(p).

Необходимо отметить, что проведенная таким образом линеаризация позволяет формально «спрятать» нелинейные свойства звена в выражения коэффициентов k_c0 и k_c1, которые нелинейно зависят от параметров воздействия m_x и _х, т. е. k_c0 = k_c0 (m_x, _x) и k_c1 = k_c1 (m_x, _x). Это следует из выражений (3.27), (3.32) и (3.34) и наглядно про-иллюстрировано в табл. 3.1. (В табл. 3.1 использована функция Ф(z) = которая называется интегралом вероятностей; t = )

Теперь с учетом выражения (3.35) реакция системы на неслучайную составляющую воздействия m_f = const определяется из уравнения статического режима

. (3.37)

Влияние же центрированной случайной составляющей воздействия на выходную координату z может быть оценено величиной дисперсии в соответствии с выражениями (3.36), (3.6) и (3.7)

(3.38)

Если в качестве выходной величины системы рассматривать сигнал x(t), который поступает на вход нелинейного звена, то выражения (3.35) и (3.36) для передаточных функций замкнутой системы по параметрам m_f и примут вид

; (3.39)

(3.40)

С учетом этого выражение (3.37) примет вид

, (3.41)

а выражение (3.38) соответственно трансформируется к виду

(3.42)

Уравнения (3.41) и (3.42) в общем случае содержат две искомые переменные (m_x, _х) и являются нелинейными. Поэтому они должны решаться совместно. Система уравнений такого типа решается либо графически, либо методом последовательных приближений. Блок-схема алгоритма нахождения решения таких уравнений методом последовательных приближений с краткими комментариями приведена на рис. 3.5.

Методика графического решения уравнений (3.41) и (3.42) в данной ситуации очевидна.

Полученные в результате решения значения коэффициентов статистической линеаризации k_c0 и k_c1 могут быть использованы для проведения дальнейших исследований нелинейной системы, например, для определения таких же статистических характеристик m и  других координат на выходе отдельных звеньев, входящих в контур системы управления, как, например, для варианта, описываемого выражениями (3.37) и (3.38).

Для иллюстрации изложенного материала рассмотрим пример.

Имеется релейная система автоматического регулирования, структурная схема которой приведена на рис. 3.6. На вход системы поступает стационарное случайное воздействие f(t), которое имеет следующие характеристики: математическое ожидание m_f = 0, кор-реляционную функцию Система характеризуется следующими параметрами: k = 2, B = 5. Требуется определить дисперсию сигнала на входе нелинейного элемен- та – .

Решение.

Выражение для спектральной плотности, соответствующее данной корреляционной функции, согласно выражениям (2.21) и (3.38), будет иметь вид

(3.43)

Р ис. 3.6. Структурная схема релейной системы автоматического регулирования

Определим передаточную функцию системы для центрированной случайной составляющей

(3.44)

где k_c1 – коэффициент статистической линеаризации.

Определим коэффициент k_c1, осуществив статистическую лине-аризацию релейной характеристики. Для данного частного случая значение k_c1 можно определить из выражения для k_с1 (см. табл. 3.1, п. 1)

. (3.45)

Найдем выражение для спектральной плотности координаты х в соответствии с выражением (3.6)

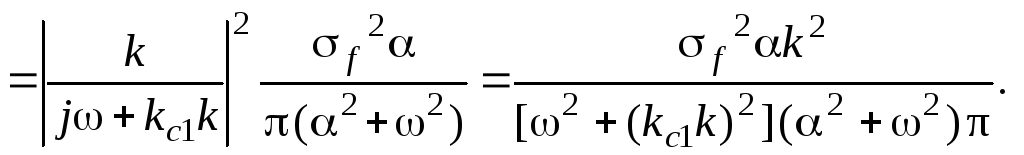(3.46)

Определим дисперсию координаты х в соответствии с выражением (3.7)

. (3.47)

Интеграл в правой части выражения (3.47) вычисляется аналогично примеру, рассмотренному в п. 5 подразд. 3.3, методом разложения на простые дроби. В результате решения после вычисления интеграла и подстановки исходных данных с использованием выражения (3.45) для коэффициента k_c1 окончательно имеем

В заключение данного подраздела необходимо отметить, что реализация метода статистической линеаризации основана на предположении, что система устойчива и в ней отсутствуют автоколебания. В противном случае наложение автоколебательного процесса на случайный сигнал может исказить параметры сигналов в разных точках системы и, в частности, их дисперсии. (В вышерассмотренном примере для упрощения задачи влияние автоколебательного процесса не учитывалось.) Для исследования режимов автоколебаний в нелинейных системах разработан и применяется специальный метод гармонической линеаризации, который подробно рассмотрен в работах [11, 12].

Сведения, изложенные в разд. 3, позволяют оценить влияние случайных воздействий на объект или систему. При этом априори подразумевается наличие математического описания объекта в той или иной форме и характеристик случайного воздействия. На практике отсутствие таких сведений зачастую является «камнем преткновения» для проведения исследований. Поэтому два следующих раздела посвящены методам получения математического описания объектов и систем и методам получения информации о входных воздействиях с учетом специфических особенностей процессов и производств пищевой промышленности.