Примеры
|
|
По определению несобственного интеграла первого рода. |
|
= |
Вычислена первообразная и подставлены пределы интегрирования. |
|
При
вычислении предела первообразной
учтем, что
сходится. | |
=
=1
и
.
Так как при вычислении получилось
число, то несобственный интеграл
|
|
По определению несобственного интеграла второго рода. |
|
= |
Учтено,
что в пределе
|
|
Так
как при вычислении получена
расходится. | |
=
.
,
то несобственный интеграл
2.
Применение признака сравнения. Не приводя теоремы о признаке сравнения, ограничимся только выводом из нее – практическим способом исследования несобственных интегралов на сходимость.
- Сравнивают подынтегральную функцию с функцией, вполне определенной для несобственных интегралов первого и второго рода.
|
Для НИ-1 |
Для НИ-2 | |
|
|
или
| |
|
| ||
|
|
так
же для
| |
-
(А1)
-(В1)
.
О несобственных интегралах от этих
функций известно:
Сравнение происходит путем определения функции, эквивалентной подынтегральной при условиях (см. тему 4, вычисление пределов):
для НИ-1:
;
;
для НИ-2
(или
)
- к точке разрыва функции,
.
Примеры
Сравните исследование на сходимость двух интегралов с одинаковыми подынтегральными функциями, но различными пределами интегрирования.
|
|
|
|
= |
= |
|
выделение главной части. |
замена сомножителей, не равных нулю, числами. |
|
Сравниваем
с
|
Сравниваем
с
|
=
,
=
,
.
НИ-1
сходится.
,
.
НИ-2
сходится.
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь бесконечной фигуры.
|
НИ-1 |
НИ-2 |
|
В
теории вероятностей и математической
статистике значительную роль играет
интеграл Пуассона – Эйлера, доказано,
что он сходится:
|
Рассмотрим
НИ-2
|
|
|
|
.
Тогда площадь под кривой Гаусса:
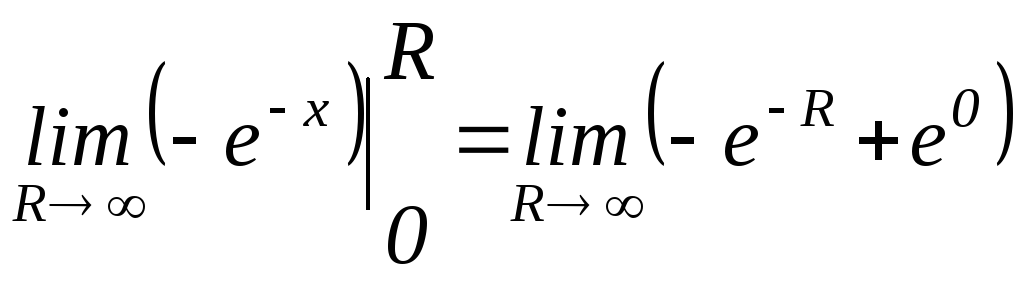равна 1.
.
Не останавливаясь подробно на
вычислении, отметим, что он сходится,
а это значит, что существует конечная
площадь под кривой, изображенной на
рисунке.
