- •Тема 6. Теория
- •Тема 6. Интегральное исчисление функции одного аргумента Неопределенный интеграл. Первообразная
- •Свойства неопределенного интеграла
- •Примеры
- •Методы интегрирования
- •1. Замена переменной (подстановка)
- •Примеры
- •Методы интегрирования
- •2. По частям
- •Примеры
- •Некоторые сведения из теории комплексных чисел и действительных многочленов
- •Примеры к теореме 1
- •Примеры к теореме 2
- •Рациональные дроби, разложение правильных рациональных дробей на сумму простейших дробей
- •Примеры
- •Интегрирование рациональных дробей
- •Правильная или неправильная дробь?
- •Тема 7. Определенные и несобственные интегралы Определенный интеграл
- •Вычисление определенных интегралов. Формула Ньютона-Лейбница
- •Особенности вычисления определенного интеграла
- •Вычисление площадей криволинейных фигур
- •Несобственные интегралы первого и второго родов. Исследование на сходимость и вычисление
- •Примеры
- •Примеры
Особенности вычисления определенного интеграла
|
При замене переменных (подстановках) |
При интегрировании по частям |
|
Замена переменных, в отличие от неопределенного интеграла, предполагает не только замену подынтегрального выражения, но и замену пределов интегрирования. |
Не следует забывать, что определенный интеграл – это число, при интегрировании по частям пределы интегрирования подставляют во все найденные функции. |
|
где
новые пределы интегрирования находят
как корни уравнений:
|
|
Примеры вычисления определенных интегралов можно найти в разделе Примеры выполнения обязательных заданий по теме 7.
Вычисление площадей криволинейных фигур
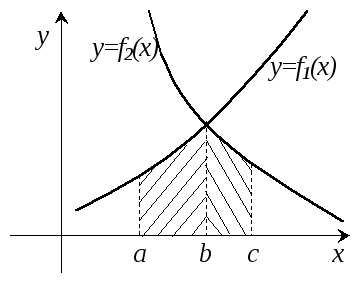
Из задачи, рассмотренной в начале темы 7, приводящей к понятию определенного интеграла, ясно, что с его помощью можно вычислять площади плоских криволинейных фигур. При этом следует различать два случая.
|
Площадь заключена между заданными кривыми. |
Площадь лежит под (над) заданными линиями (между линиями и осью ОХ). |
|
|
|
|
Тогда, определив точки пересечения линий, т.е. пределы интегрирования, можно найти площадь как разность площадей под вышележащей и нижележащей кривой. |
По
рисунку видно, что в данном случае
общая площадь складывается из площадей
под линией
|
|
по свойству линейности
|
|
|
Среди геометрических приложений определенного интеграла можно еще отметить :
|
Вычисление
длины дуги
кривой
от точки А до точки В : |
|
Вычисление
объемов тел вращения:
|
Несобственные интегралы первого и второго родов. Исследование на сходимость и вычисление
Чтобы существовал определенный интеграл, то есть существовал предел интегральной суммы, должны выполняться два условия:
|
1. Отрезок (интервал) интегрирования кончен. |
2.
Подынтегральная функция
| |
|
Cправка.
В точке
Практически для определения точки разрыва надо найти точки, которые не входят в область допустимых значений, например, такие, в которых знаменатель обращается в ноль. | ||
|
Если не выполняется одно из условий (но не оба сразу), определенный интеграл не существует и вводится понятие несобственного интеграла (НИ).
| ||
|
1.
Отрезок интегрирования бесконечен,
подынтегральная функция
|
2.
Подынтегральная функция
| |
|
|
| |
|
Несобственный интеграл первого рода – по бесконечному отрезку (НИ-1) |
Несобственный интеграл второго рода – от разрывной функции (НИ-2) | |
|
Несобственные интегралы определяются как пределы, к которым стремятся определенные интегралы при соответствующих условиях. | ||
|
|
| |
|
Третий случай (для НИ и первого и второго рода) сводится к сумме двух первых. |
Квадратными скобками отмечены точки разрывов подынтегральной функции. | |
|
Если
пределы, стоящие в правых частях
равенств, определяющих несобственные
интегралы, существуют
и конечны,
то несобственные интегралы сходятся,
в противном случае расходятся
(предел не существует или бесконечен
-
| ||
Сходящиеся несобственные интегралы обладают всеми свойствами определенных интегралов.
Вопрос о сходимости несобственных интегралов можно решить двумя способами.
1.
Непосредственное вычисление. Если несложно определить первообразную, то можно вычислить определенный интеграл, затем найти его предел при поставленных условиях и сделать заключение:
если при вычислении несобственного интеграла получено любое число, то он сходится (к этому числу);
если получена
 или предел не существует, то несобственный
интегралрасходится.
или предел не существует, то несобственный
интегралрасходится.