Методы интегрирования

2. По частям

 - - формула интегрирования по частям.

Основная идея метода интегрирования по частям: разбить подынтегральное выражение заданного интеграла на части итаким образом, чтобы интегралоказалсяпроще исходного.

Существует класс функций, для которого разбиение на части вполне предопределено. Это произведение трансцендентных функций на многочлен. Пусть - многочленn-го порядка. Например, - линейный,- квадратный, и т. д. Заметим, что при дифференцировании степень многочлена понижается на единицу.

Исходный интеграл	Разбиение на части	По формуле
		- степень многочлена понижается на единицу.

После однократного интегрирования по частям получают интеграл того же вида, но с более низкой степенью многочлена. После n-кратного интегрирования по частям приходят к интегралам вида ,,, сводящимся к табличным умножением напод знаком дифференциала.

Исходный интеграл	Разбиение на части	По формуле
		;=
(и другие обратные тригонометрические функции).

Несмотря на повышение степени многочлена при интегрировании, в данном случае, выбирая в качестве части трансцендентную функцию, мы добиваемся того, что дифференцирование приводит к функциям, не содержащим трансцендентности.

Примеры

Интегрирование по частям.

 ==	Разбиваем интеграл на части в соответствии с рекомендациями.
=	По формуле интегрирования по частям.
==.	Алгебраические преобразования приводят к окончательному ответу. 

 ==	Разбиваем интеграл на части в соответствии с рекомендациями.
=	По формуле интегрирования по частям.
= =	Для вычисления интеграла применяем "внесение под знак дифференциала":  

 Метод интегрирования по частям можно применять совместно с методом замены переменных.

	Заменяем переменную. - по формуле понижения степени.
	Полученный интеграл разбиваем на сумму двух интегралов. Первый – табличный: , второй вычисляем по частям.
=	Разбиваем интеграл на части в соответствии с рекомендациями.
		По формуле интегрирования по частям. 

Некоторые сведения из теории комплексных чисел и действительных многочленов

Справка о комплексных числах.

Комплексное число: , комплексно-сопряженное ему число(или наоборот). Здесь- действительные числа,-мнимая единица. Очевидно, что и т.д. Можно убедиться, что.

• Действительный многочлен (полином):

,

где - коэффициенты, действительные числа.

, - линейный,- квадратный и т.д.

• Каждое число , которое обращает многочлен в ноль:, называется корнем этого многочлена.Или: корни многочлена это решения уравнения .

Теоремы о действительных многочленах.

 Теорема 1.Многочленn-го порядка имеет ровноnкорней, которые могут быть как действительными, так и комплексными числами.

Примеры к теореме 1

• Рассмотрим квадратный многочлен и найдем его корни.дискриминант. Отрицательный дискриминант означает, что многочлен имеет комплексные корни.. Обозначими назовеммнимой единицей. По общему правилу корни - комплексно-сопряженные числа. Можно записать их и так:. Таким образом, многочлен второго порядка имеет два корня.

• Рассмотрим многочлен и определим его корни.

	После алгебраических преобразований ясно, что многочлен четвертого порядка имеет два корня и два корня. Такие корни называютсякратными. В данном случае кратность каждого из корней - два.

 - Обратите внимание! Кратность корня указывается степенью сомножителя, из равенства нулю которого он получается.

 Теорема 2.Многочленn-го порядка можно представить в виде произведения ("разложить по корням"):

,

где -действительные корни многочлена, -кратность соответствующего действительного корня;

- квадратный трехчлен с дискриминантом, т.е. имеющий пару комплексно-сопряженных корней, - кратность каждого комплексного корня.
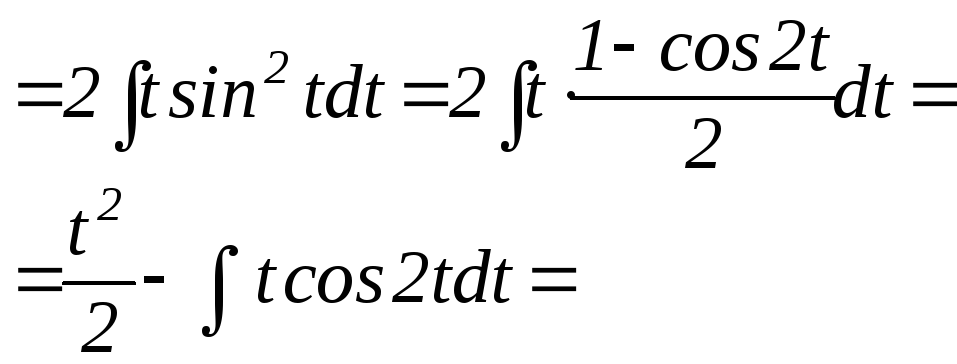