Тема 6. Теория

Тема 6. Интегральное исчисление функции одного аргумента Неопределенный интеграл. Первообразная

Если основной задачей дифференциального исчисления является поиск производной (или дифференциала) функции, то интегральное исчисление решает обратную задачу: восстанавливает функцию по заданной производной ли дифференциалу.

• Функция 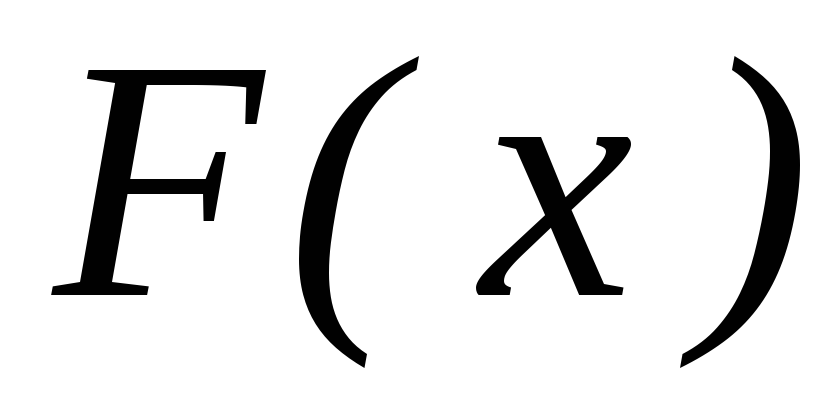называетсяпервообразной для функции 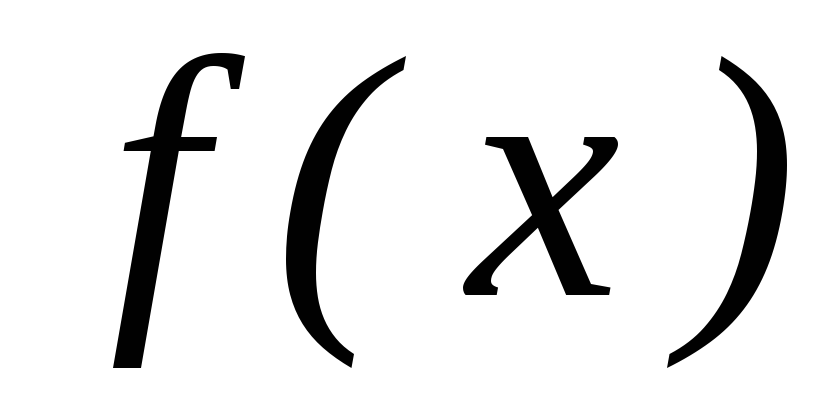на данном промежутке, если в каждой точке этого промежутка:

или, что то же самое, .

• Совокупность всех первообразных функции 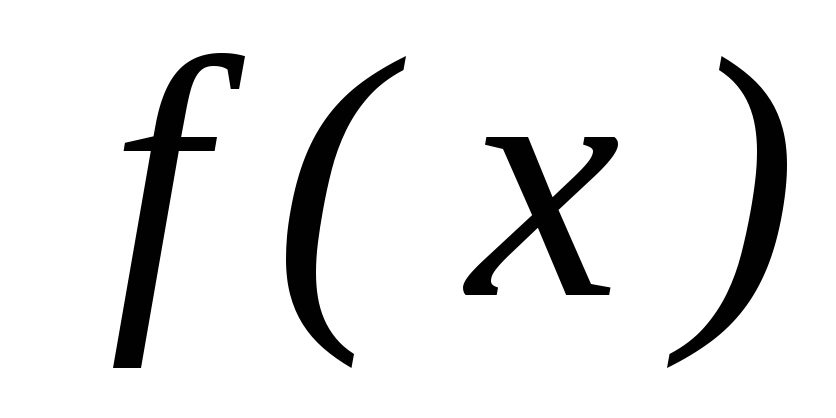, отличающихся только произвольными постоянными (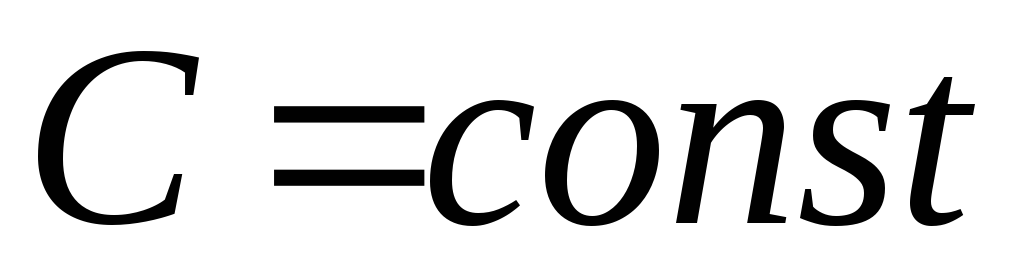), называется неопределенным интегралом функции и обозначается:

.

Здесь - подынтегральное выражение,дифференциал первообразной; - подынтегральная функция,производная первообразной.  - В результате вычисления неопределенного интеграла мы находим функцию по ее дифференциалу, отсюда следует способ проверки – если продифференцировать найденную первообразную, то следует получить подынтегральное выражение.

Свойства неопределенного интеграла

1 Из определения следует: и

2 .

Свойства 1 и 2 подтверждают, что интегрирование и дифференцирование – взаимно обратные операции.

3 ;

.

Свойство 3 показывает, что интегрирование – линейная операция. Это свойство может быть распространено на любое конечное число слагаемых:

.

4 Свойство инвариантности неопределенного интеграла (следует из свойства инвариантности дифференциала функции, см. тему 5).

Если и, то.

Иными словами, вид первообразной не зависит от того, является ли переменной интегрирования функция или независимая переменная.

 - Обратите внимание! Это свойство будет основным при вычислении неопределенных интегралов методом внесения под знак дифференциала (см. далее).

Таблица основных неопределенных интегралов

(обязательна для запоминания)

Подынтегральная функция			Неопределенный интеграл
1	Степенная
	Частные случаи
2	Показательная
	Экспонента
3	Логарифмическая
4	Тригонометрические
5	Обратные тригонометрические
6	Ареасинус или "длинный логарифм"

Следующие интегралы для запоминания не обязательны, так как могут быть получены с помощью основной таблицы и методов интегрирования, но встречаются достаточно часто:

7
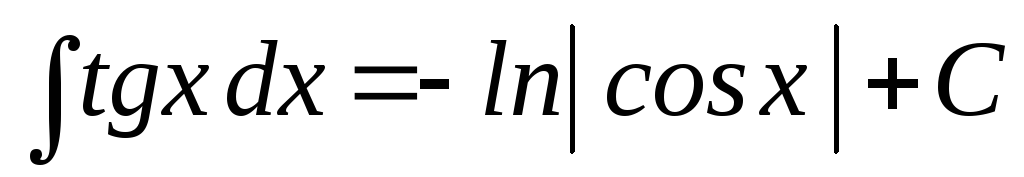
8
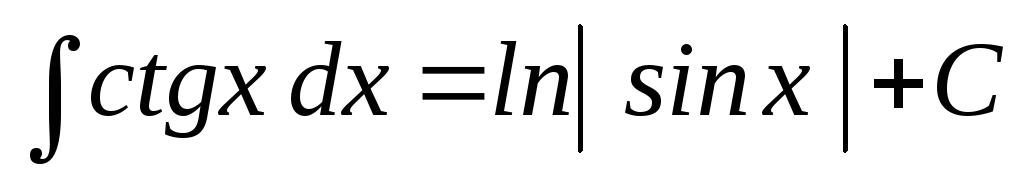
9
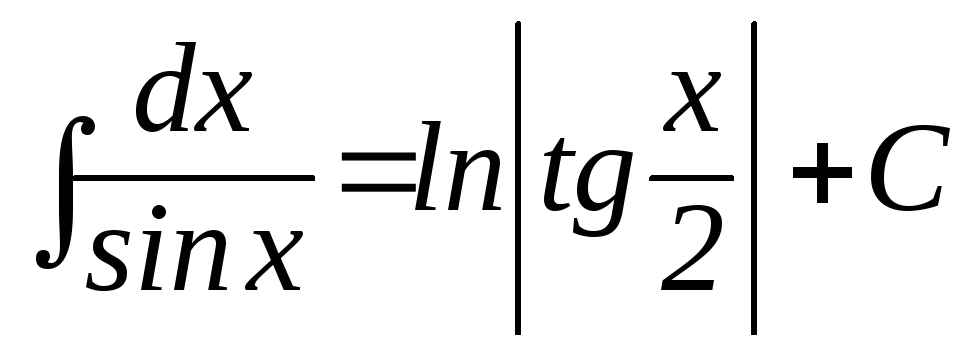
10
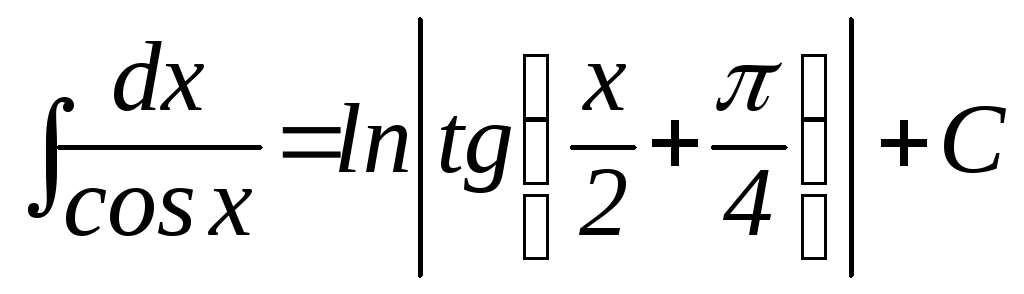
11

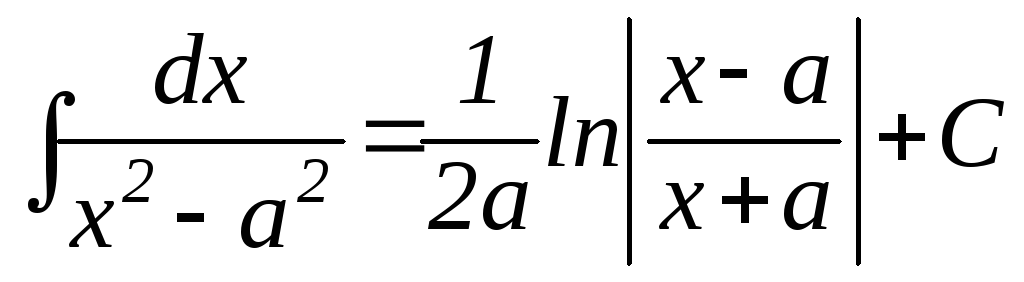
Любой интеграл из таблицы можно проверить дифференцированием. Например, 9:

.

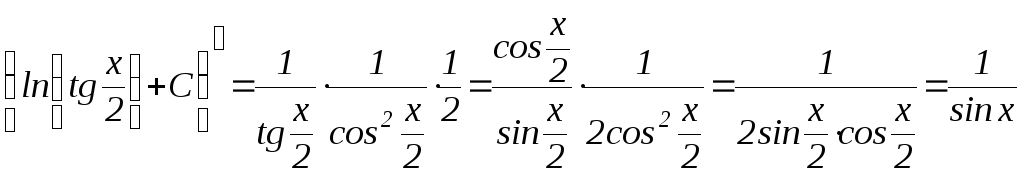Производная первообразной равна подынтегральной функции.

Используя свойства неопределенных интегралов и таблицу, можно непосредственно интегрировать некоторые функции.

Примеры

Непосредственное интегрирование.

Самостоятельно определите табличные интегралы, которые использованы при решении примеров.

   

   

 

 - Обратите внимание на знаки под корнями в примерах 4 и 5. Следующие примеры иллюстрируют сочетание применение свойства 3 (интеграл от алгебраической суммы функций равен сумме интегралов от этих функций) и непосредственного интегрирования.

 

 



 - Интегралы от четных степеней синуса и косинуса вычисляются по тригонометрической формуле понижения степени.



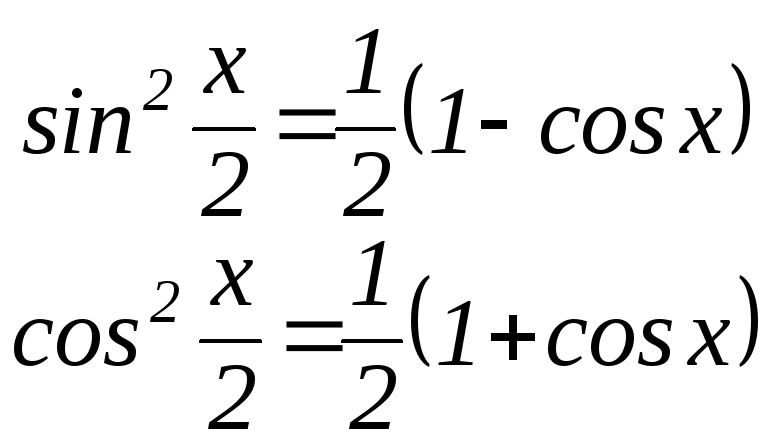
Применение свойства инвариантности.

   

Функции, интегрируемые непосредственно, не исчерпывают даже основных элементарных функций, не говоря уже о сложных. Например, среди табличных нет интегралов от трансцендентных функций и т.п.

Задача интегрирования принципиально сложнее задачи дифференцирования. В дифференциальном исчислении имелось конструктивное определение производной и ряд правил дифференцирования (суммы, произведения, частного, сложных и обратных функций). Зная эти правила и таблицу производных, можно найти производную любой функции.

В интегральном исчислении интеграл определяется не конструктивно, правил для интегрирования произведения, частного и т. п. нет. Имеются лишь отдельные приемы (методы), позволяющие интегрировать отдельные классы функций. Эти методы мы рассмотрим ниже.