
Особенности вычисления определенного интеграла
|
При замене переменных (подстановках) |
При интегрировании по частям |
|
Замена переменных, в отличие от неопределенного интеграла, предполагает не только замену подынтегрального выражения, но и замену пределов интегрирования. |
Не следует забывать, что определенный интеграл – это число, при интегрировании по частям пределы интегрирования подставляют во все найденные функции. |
|
где
новые пределы интегрирования находят
как корни уравнений:
|
|
Примеры вычисления определенных интегралов можно найти в разделе Примеры выполнения обязательных заданий по теме 7.
Вычисление площадей криволинейных фигур
Из задачи, рассмотренной в начале темы 7, приводящей к понятию определенного интеграла, ясно, что с его помощью можно вычислять площади плоских криволинейных фигур. При этом следует различать два случая.
|
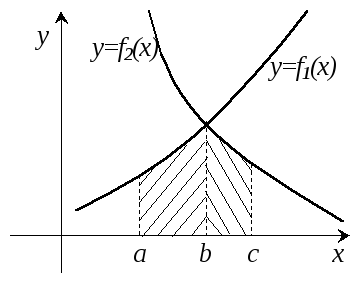
Площадь заключена между заданными кривыми. |
Площадь лежит под (над) заданными линиями (между линиями и осью ОХ). |
|
|
|
|
Тогда, определив точки пересечения линий, т.е. пределы интегрирования, можно найти площадь как разность площадей под вышележащей и нижележащей кривой. |
По
рисунку видно, что в данном случае
общая площадь складывается из площадей
под линией
|
|
по свойству линейности
|
|
|
Среди геометрических приложений определенного интеграла можно еще отметить :
|
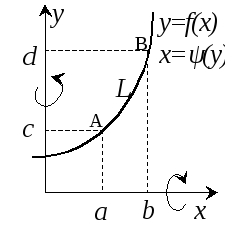
Вычисление
длины дуги
кривой
от точки А до точки В : |
|
Вычисление
объемов тел вращения:
|
Применение определенного интеграла в экономических задачах
Пусть
функция z=f(t)
описывает
изменение производительности некоторого
производства с течением времени. Найдем
объем продукции
![]() ,
произведенной за промежуток времени[0;Т].
,
произведенной за промежуток времени[0;Т].
Если
производительность не изменяется с
течением времени (f(t)
– постоянная
функция), то объем продукции
![]() ,
произведенной за некоторый промежуток
времени[t,
t+t],
находится по формуле:
,
произведенной за некоторый промежуток
времени[t,
t+t],
находится по формуле:
![]() =f(t)
t.
=f(t)
t.
В
общем случае справедливо приближенное
равенство
![]()
![]() f()t,
где [t,
t+t],
которое
оказывается тем более точным, чем меньше
t.
f()t,
где [t,
t+t],
которое
оказывается тем более точным, чем меньше
t.
Разобьем отрезок [0; T] на промежутки времени точками:
0=t0<t1<t2<<tn=T.
Для величины объема продукции
![]() ,
произведенной за промежуток времени
[ti-1,
ti],
имеем
,
произведенной за промежуток времени
[ti-1,
ti],
имеем
![]() =f(i)
ti,
где
i[ti-1,
ti],
ti=ti-ti-1,
i=1,2,,n.
Тогда
=f(i)
ti,
где
i[ti-1,
ti],
ti=ti-ti-1,
i=1,2,,n.
Тогда
![]()
При
стремлении
![]() к нулю каждое из использованных
приближенных равенств становится все
более точным, поэтому :
к нулю каждое из использованных
приближенных равенств становится все
более точным, поэтому :
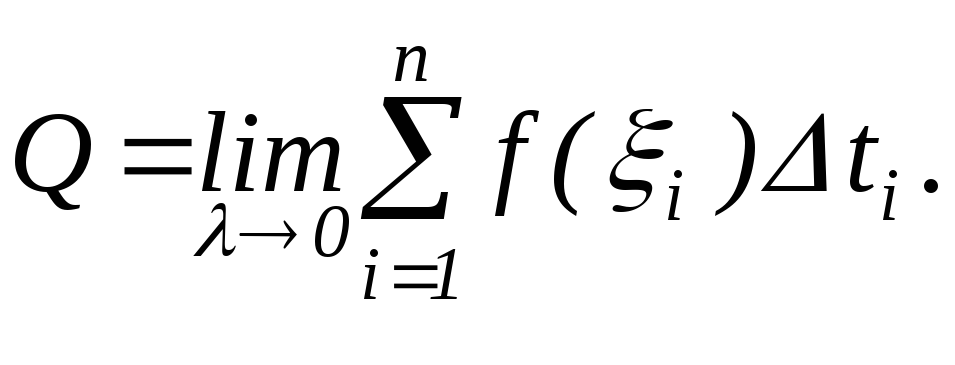
По определению определенного интеграла, окончательно получаем:
![]()
т.е. если f(t)
– производительность труда в моментt, то![]() есть объем выпускаемой продукции за
промежуток[0; T].
есть объем выпускаемой продукции за
промежуток[0; T].
Сравнение данной задачи с задачей о площади криволинейной трапеции показывает, что величина и объем продукции, произведенной за промежуток времени [0; T], численно равен площади под графиком функции z=f(t), описывающей изменение производительности труда с течением времени, на промежутке [0; T].
Экономический смысл определенного интеграла - объем произведенной продукции при известной функции производительности труда.
Рассмотрим другие примеры использования интеграла в экономике.
1.
Если в
функции Кобба-Дугласа
считать, что затраты труда линейно
зависят от времени, а затраты капитала
неизменны, то она примет вид
![]() .Тогда объем
выпускаемой продукции за Т
лет составит:
.Тогда объем
выпускаемой продукции за Т
лет составит:
![]()
Найдем
объем продукции, произведенной за 4
года, если функция Кобба-Дугласа имеет
вид
![]() .
.
|
|
Объем произведенной продукции Q. Интегрируем по частям. |
|
| |
2. Исследуя кривую Лоренца – зависимость процента доходов от процента имеющего их населения (кривую ОВА), мы можем оценить степень неравенства в распределении доходов населения. При равномерном распределении доходов кривая Лоренца вырождается в прямую – биссектрису ОА, поэтому площадь фигуры ОАВ между биссектрисой ОА и кривой Лоренца, отнесенная к площади треугольника ОАС (коэффициент Джини), характеризует степень неравенства в распределении доходов населения. Высокое значение этого коэффициента показывает существенно неравномерное распределение доходов среди населения в рассматриваемой стране.
По
данным исследований в распределении
доходов в одной из стран кривая Лоренца
ОВА
может быть описана уравнением
![]() ,
гдех
– доля населения, у
– доля доходов населения. Вычислить
коэффициент Джини.
,
гдех
– доля населения, у
– доля доходов населения. Вычислить
коэффициент Джини.


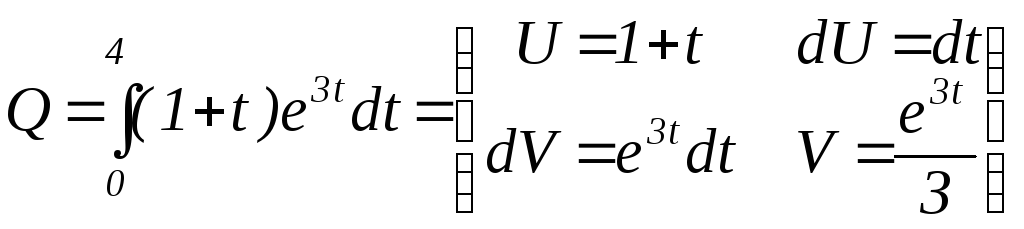 =
=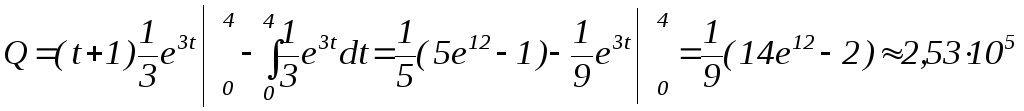 у.ед.
у.ед.