kornil / ФУБ семестр 2 / Высшая математика 2 семестр / TEMA7 / Теория2
.docТема 7. Теория
Несобственные интегралы первого и второго родов.
Исследование на сходимость и вычисление
Чтобы существовал определенный интеграл, то есть существовал предел интегральной суммы, должны выполняться два условия:
|
1. Отрезок (интервал) интегрирования кончен. |
2.
Подынтегральная функция
|
|
|
Cправка.
В точке
Практически для определения точки разрыва надо найти точки, которые не входят в область допустимых значений, например, такие, в которых знаменатель обращается в ноль. |
||
|
Если не выполняется одно из условий (но не оба сразу), определенный интеграл не существует и вводится понятие несобственного интеграла (НИ).
|
||
|
1.
Отрезок интегрирования бесконечен,
подынтегральная функция
|
2.
Подынтегральная функция
|
|
|
|
|
|
|
Несобственный интеграл первого рода – по бесконечному отрезку (НИ-1) |
Несобственный интеграл второго рода – от разрывной функции (НИ-2) |
|
|
Несобственные интегралы определяются как пределы, к которым стремятся определенные интегралы при соответствующих условиях. |
||
|
|
|
|
|
Третий случай (для НИ и первого и второго рода) сводится к сумме двух первых. |
Квадратными скобками отмечены точки разрывов подынтегральной функции. |
|
|
Если
пределы, стоящие в правых частях
равенств, определяющих несобственные
интегралы, существуют
и конечны,
то несобственные интегралы сходятся,
в противном случае расходятся
(предел не существует или бесконечен
-
|
||
на
не имеет разрывов второго рода.
имеется разрыв второго рода, если
хотя бы один из односторонних пределов
функции в этой точке бесконечен или
не существует:
(см. тему 4, схема классификации
разрывов).
на нем непрерывна.
имеет хотя бы один разрыв второго
рода на
,
отрезок интегрирования конечен.
(А)
(В)
(А1)
(В1)
).
Сходящиеся несобственные интегралы обладают всеми свойствами определенных интегралов.
Вопрос о сходимости несобственных интегралов можно решить двумя способами.
1.
Непосредственное вычисление. Если несложно определить первообразную, то можно вычислить определенный интеграл, затем найти его предел при поставленных условиях и сделать заключение:
-
если при вычислении несобственного интеграла получено любое число, то он сходится (к этому числу);
-
если получена
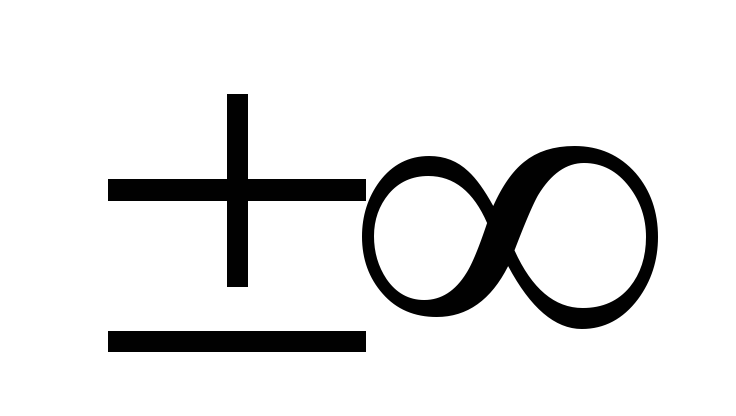или предел не существует, то несобственный
интеграл расходится.
ПРИМЕРЫ
|
|
По определению несобственного интеграла первого рода. |
|
= |
Вычислена первообразная и подставлены пределы интегрирования. |
|
При
вычислении предела первообразной
учтем, что
сходится. |
|
=
=1
и
.
Так как при вычислении получилось
число, то несобственный интеграл
|
|
По определению несобственного интеграла второго рода. |
|
= |
Учтено,
что в пределе
|
|
Так
как при вычислении получена
расходится. |
|
=
.
,
то несобственный интеграл
2.
Применение признака сравнения. Не приводя теоремы о признаке сравнения, ограничимся только выводом из нее – практическим способом исследования несобственных интегралов на сходимость.
- Сравнивают подынтегральную функцию с функцией, вполне определенной для несобственных интегралов первого и второго рода.
|
Для НИ-1 |
Для НИ-2 |
|
|
|
или
|
|
|
|
||
|
|
так
же для
|
|
-
(А1)
- (В1)
.
О несобственных интегралах от этих
функций известно:
Сравнение происходит путем определения функции, эквивалентной подынтегральной при условиях (см. тему 4, вычисление пределов):
-
для НИ-1:
;
;
-
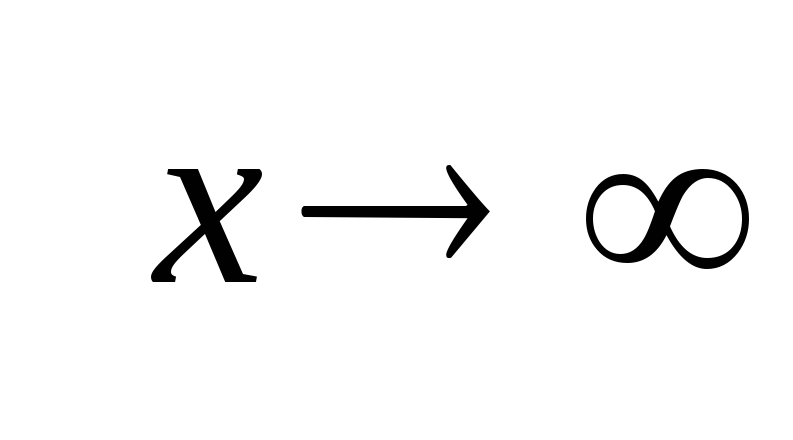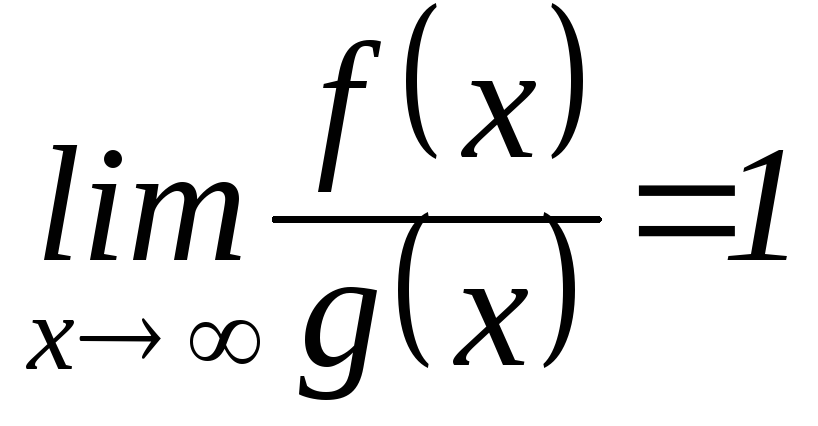для НИ-2
(или
)
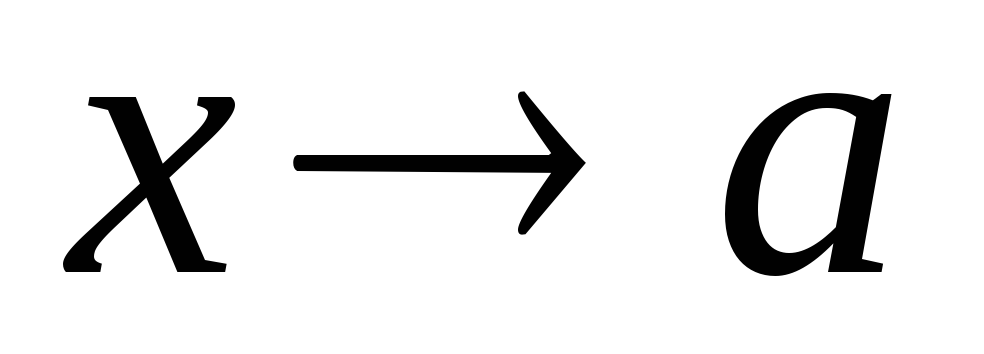- к точке разрыва функции,
.
ПРИМЕРЫ
Сравните исследование на сходимость двух интегралов с одинаковыми подынтегральными функциями, но различными пределами интегрирования.
|
|
|
|
= |
= |
|
выделение главной части. |
замена сомножителей, не равных нулю, числами. |
|
Сравниваем
с
|
Сравниваем
с
|
=
,
=
,
.
НИ-1
сходится.
,
.
НИ-2
сходится.
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь бесконечной фигуры.
|
НИ-1 |
НИ-2 |
|
В
теории вероятностей и математической
статистике значительную роль играет
интеграл Пуассона – Эйлера, доказано,
что он сходится:
|
Рассмотрим
НИ-2
|
|
|
|
.
Тогда площадь под кривой Гаусса:
равна 1.
.
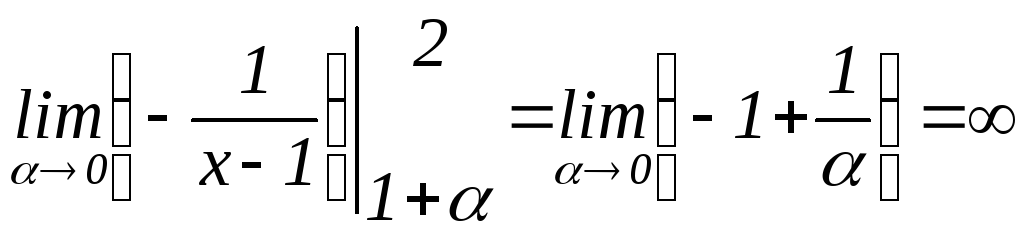
Не останавливаясь подробно на
вычислении, отметим, что он сходится,
а это значит, что существует конечная
площадь под кривой, изображенной на
рисунке.
