Примеры выполнения обязательных заданий по теме 5
Задание 1. 1) Найти производную функции, используя основные правила дифференцирования.
2) Найти производную сложной функции.
3) Найти производную логарифмическим дифференцированием.
4) Найти производную параметрически заданной функции.
5) Найти производную неявно заданной функции.
6) Найти дифференциал функции при данном значении х.
Примеры
Производную заданной функции будем находить, используя правила дифференцирования произведения, частного и правило вынесения константы за знак дифференцирования. Эти правила записаны справа от задания.
|
|
|
|
|
|
|
+ |
|
|
= |
|
,
С
– const;
+
,
С
– const;
-
=
,
учтем, что
- const
и
.
- при выполнении задания 1, т.е. при вычислении производных желательно не делать никаких упрощений полученных выражений.
|
|
В этом примере надо вычислить производную сложной функции. Она представляет собой произведение производных функций, из которых |
|||
|
|
составлена за-данная функция. |
|||
|
|
||||
|
|
Заданная функция является степенно-показательной, ее производной в таблице нет. |
|||
|
|
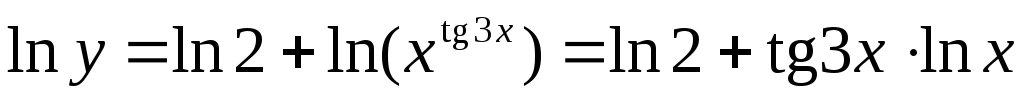
Применим логарифмическое дифференцирование. Для этого прологарифмируем заданную функцию. |
|||
|
|
Возьмем
производные от обеих частей полученного
равенства, учитывая что
|
|||
|
|
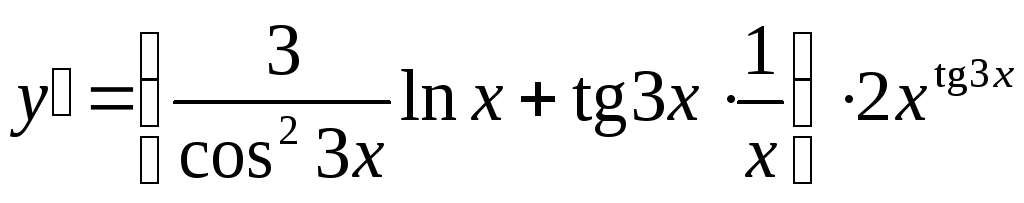
Выразим
|
|||
;
;
или
из полученного равенства.