
- •Основные понятия Matlab
- •ВЫЧИСЛЕНИЯ
- •Особенности ввода команд и данных
- •Элементы данных в ML
- •Переменные в ML
- •Выражения
- •ОПЕРАЦИИ
- •Простейшие арифметические операции (АО)
- •Операции отношения
- •Логические операции
- •Приоритет элементарных операций в ML
- •Основные математические функции MatLab
- •Ввод и вывод информации. Операторы ввода/вывода
- •<имя переменной>= input(<текст>)
- •Для этого используют несколько способов.
- •disp(strcat('x=', num2str(x)))
- •y=sprintf('x=%3.1f ', x)
- •%[флаг][ширина поля вывода][точность] тип (спецификатор) формата
- •x=<значение>; y=<значение>; z=<значение>;
- •>> sprintf('x=%4.2f; y=%5.3f; z=%d;',x,y,z)
- •Условный оператор
- •МНОЖЕСТВЕННЫЙ ВЫБОР
- •Определенные циклы
- •Неопределенные циклы
- •ЗАДАНИЕ И ОБРАБОТКА ВЕКТОРОВ И МАТРИЦ
- •Способы задания векторов
- •<имя пер.>=[<значение1> <значение2> ….<значениеN>]
- •<имя пер.>=<нач. значение>:<шаг>:<конечное значение>
- •linspace (<нач. значение>,<кон. значение>,<кол. значений>)
- •Задание матриц
- •Операции
- •Операции над векторами – то же самое
- •Поэлементные операции
- •ОСОБЫЕ МАТРИЦЫ
- •Матрица случайных чисел:
- •Автоматическое заполнение матриц. Формирование матрицы блоками
- •>> X=[eye(4), 3*ones(4); 5*ones(4),9*eye(4)]
- •Дополнительно из задач
- •Применение функций обработки данных к векторам и матрицам
- •>> help datafun
- •Функции для векторов
- •Для матриц
- •Сумма элементов в столбцах матрицы:
- •Сумма элементов в строках матрицы:
- •Сумма элементов вектора:
- •Получение из матрицы вектора
- •Произведение элементов матрицы по столбцам:
- •Произведение элементов матрицы по строкам:
- •Максимальное значение в каждом столбце:
- •Максимальное значение в каждой строке:
- •Максимум во всей матрице
- •Наименьшее значение:
- •Среднее значение
- •Среднее арифметическое в столбцах. Результат – вектор-строка из средних арифметических в каждом столбце:
- •В строках
- •Сортировка.
- •по убыванию:
- •по убыванию
- •’’Зеркальное’’ отображение матрицы относительно вертикальной оси:
- •’’Зеркальное’’ отображение матрицы относительно горизонтальной оси:
- •Примеры использования
- •среднего и суммы:
- •Для матрицы:
- •Найти наибольшее значение среди элементов <8
- •Для матрицы
- •Сумму элементов побочной диагонали
- •Сумму элементов главной диагонали
- •Нормы матрицы
- •>> max_stolb=max(sum(abs(В)))
- •Найти среднее арифметическое в каждом столбце
- •Пр. Удалить максимальный элемент в векторе
- •Пр. Вставить значение 100 в вектор после элемента с номером k=3
- •Пр. В матрице поменять местами столбцы с минимальным и максимальным элементами.
- •[m_min,jmin]=min(min(b));
- •[m_max,jmax]=max(max(b));
- •buf=b(:, jmin);
- •Пр. Поменять порядок следования элементов в векторе
- •Еще полезные функции all, any и find и их использование
- •Для вектора
- •Получить индексы элементов, равных 2
- •Графика ML
- •Построение простейших графиков функций одной переменной Графики параметрических и кусочно-заданных функций
- •Plot(x, y, ‘<тип маркера, обозначение цвета и тип линий>’)
- •Отображение нескольких кривых на одном графике (в одних осях)
- •hold off
- •Вывод нескольких графиков в одном графическом окне
- •subplot(m, n, p),
- •Изменение масштаба графика
- •Диаграммы
- •Трехмерные графики
- •Т=-2:0.01:2; % задали вектор значений аргумента
- •Построение поверхности в 3-мерном пространстве
- •% Поверхность z=f(x,y)
- •Решение типовых математических задач
- •Файлы функций
- •function [рез.1, рез.2…рез.N] = <имя функции> (пар.1, пар.2,…пар.N)
- •[y1, y2,…,yn]=<имя функции>(<список вх. факт. параметров>)
- •<имя функции>(<список входных фактических параметров>)
- •function <имя функции> (пар.1, пар.2,…пар.n)
- •Отличия файла-функции от скрипт-файла
- •Примеры
- •function y=mysin(x)
- •Пример функции с 3 выходными параметрами
- •Использование функций для задач вычислительной математики
- •Построение графика функций
- •Действия с полиномами (многочленами)
- •Решение системы линейных уравнений.
- •Численное интегрирование
- •[i, n]=quadl (fun, a, b, tol, trace),
- •Решение уравнений
- •Нахождение минимума функции на заданном отрезке
- •Функция eval
- •Файл меню
- •while k~=6
- •Символьные вычисления в ML
- •Преобразование символьных выражений
- •Построение графиков символьных функций
- •Решение уравнений и систем
- •Решение дифференциальных уравнений и систем
- •Вычисление пределов
- •Определение производной
- •Вычисление интеграла

В математическом виде:
>> pretty(collect(pol,y))
2
((x + 1) + 1) y + 2 x - 2
5). Функция factor (expr) раскладывает символьное выражение на простые
множители
>> factor (pol) % Преобразование функции pol=y*(x+1)^2+(x-2)+(x+y) ans =
y*x^2+2*y*x+2*y+2*x-2
>> factor (x^3-1) % Разложение функции x^3-1
ans =
(x-1)*(x^2+x+1)
>> factor (36) % Разложение числа 36
ans =
2 2 3 3
Построение графиков символьных функций
Рассмотренные ранее графические возможности ML дополняются средствами построения графиков функций, заданных в символьном виде (не надо формировать вектор или матрицу, содержащие значения функции).
График функции одной переменной строится командой ezplot (fun, Xmin, Xmax). График функции fun будет построен на отрезке
[Xmin, Xmax], а если отрезок не указан, то берется интервал [-2*pi, 2*pi].
>>syms x
>> f=cos(x/2)+1/5*cos(5*x)
f =
cos(1/2*x)+1/5*cos(5*x)
>> ezplot (f) % График на отрезке [-2*pi, 2*pi]
или
>> ezplot('cos(x/2)+1/5*cos(5*x)')
39
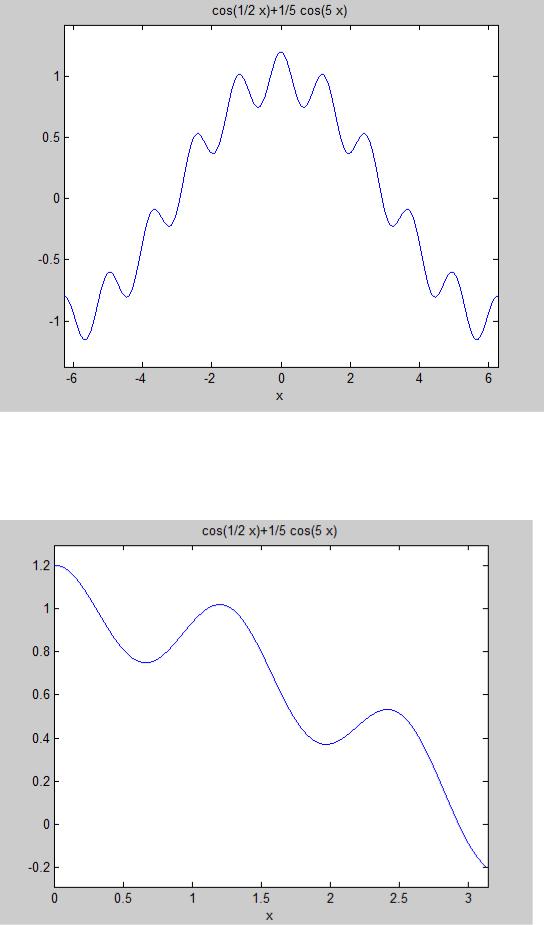
>> ezplot (f, 0, pi) такое обращение возможно не во всех версиях Матлаба,
или можно записать
>> ezplot (f, [0 pi])
Используя режим наложения графиков с помощью команды hold on, можно
последовательно строить несколько графиков в одних осях.
40
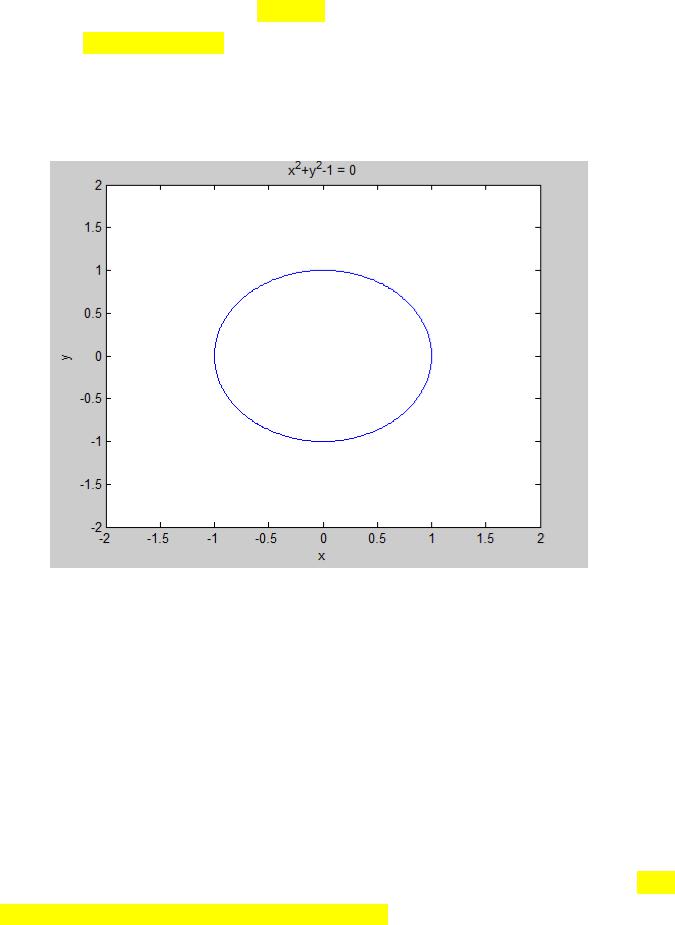
Особенностью функции ezplot () является возможность создания графика функции, заданной неявно. Ezplot (fun, Xmin, Xmax, Ymin, Ymax) строит график функции f (x,y) = 0, [Xmin,Xmax] – пределы изменения первого по алфавиту аргумента, [Ymin,Ymax] – пределы изменения второго по алфавиту аргумента.
>> ezplot ('x^2+y^2-1', [-2 2 -2 2])
Аналогично функциям polar (построения графиков вида r=r(ψ), a≤ψ≤b в полярной системе
координат), surf, mesh, plot3 для символьных функций существуют функции
ezpolar – построение в полярных координатах
ezsurf – построение поверхности вида z=f(x,y)
ezmesh – строит поверхность с нанесением контурных линий
ezplot3 - строит поверхность, заданную параметрически.
Решение уравнений и систем
В ML существуют средства для решения уравнений численными методами.
Кроме того, есть возможность решать уравнения в символьном виде. Функция solve (expr, var) возвращает решение уравнения, задаваемого выражением expr
относительно переменной var. Ищутся корни уравнения или нули выражения.
41
>> syms a b c x
%Решается уравнение a*x^2+b*x+c=0 отн. х
%Если коэффициенты не заданы, то решение в общем виде
%Если коэффициенты заданы, то результат – числовое значение
>> y=solve (a*x^2+b*x+c, x)
y =
-(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a)
>> pretty(y) |
|
|
||
+- |
|
-+ |
|
|
| |
|
2 |
1/2 |
| |
| |
|
b + (b - 4 a c) |
| |
|
| |
- ------------------- |
| |
||
| |
|
2 a |
| |
|
| |
|
|
| |
|
| |
|
2 |
1/2 | |
|
| |
|
b - (b - 4 a c) |
| |
|
| |
- ------------------- |
| |
||
| |
|
2 a |
| |
|
+- |
|
-+ |
|
|
Если второй параметр не указан, то по умолчанию уравнение решается относительно х.
>> y=solve ('a*x^2+b*x+c=0')
y =
-(b + (b^2 - 4*a*c)^(1/2))/(2*a) -(b - (b^2 - 4*a*c)^(1/2))/(2*a)
Видим, что уравнение решается в общем виде.
Пусть задан полином, найдем корни полинома 3*x4+2*x3-x2-15*x+7 в
числовом и символьном виде:
%выч. корн.пол 3*x^4+2*x^3-x^2-15*x+7
p=[3 2 -1 -15 7];
42
disp('корни пол')
x=roots(p)
disp('символьные вычисления ')
disp('корни полинома ')
syms x
z=solve(3*x^4+2*x^3-x^2-15*x+7)
zs=vpa(z)
Получим на экране:
корни пол x =
-1.2505 + 1.4296i -1.2505 - 1.4296i 1.3581 0.4762
символьные вычисления корни полинома
z =
|
1.3581107410504754041265449373916 |
|
|
0.4762357236114296167745354966965 |
|
|
1.4296306305875367633296037188572*i |
- |
1.2505065656642858437838735503774 |
|
|
- |
1.4296306305875367633296037188572*i |
- |
1.2505065656642858437838735503774
zs =
|
1.3581107410504754041265449373916 |
|
|
0.4762357236114296167745354966965 |
|
|
1.4296306305875367633296037188572*i |
- |
1.2505065656642858437838735503774 |
|
|
- |
1.4296306305875367633296037188572*i |
- |
1.2505065656642858437838735503774
>> solve (2*x^3-x-1)
43
