ОПЕРАЦИИ

С числовыми данными в ML можно выполнять обычные арифметические операции и вычислять значения функций.

Простейшие арифметические операции (АО)

На текущий момент не учитываем матричные операции.

К арифметическим операциям в ML относятся: cложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^) (это не все операции). Приоритеты АО:

возведение в степень;

умножение, деление;

сложение, вычитание.

Все арифметические операции являются “матричными” и осуществляются по

К операциям отношения в ML относятся: равно (= =), не равно (~ =), меньше (<), меньше или равно (<=), больше (>), больше или равно (>=).

Операции отношения используются для сравнения двух операндов (пока рассматриваем только числа). Результатом операции отношения может быть соответственно число 1- «истина» или 0 - «ложь».

В ML существует возможность построения логических выражений с помощью логических операторов и логических операций. Логические операции предназначены для выполнения поэлементных логических операций над векторами и матрицами одинаковых размеров. К логическим операциям относятся логическое И (&), логическое ИЛИ (|), логическое НЕ ( ).

Как и в операциях отношения, результатом логических операций являются значения 0 (ложь) или 1 (истина).

Вместо логических операций можно пользоваться логическими операторами

8

(функциями) and, or, not соответственно. Логические операторы определены над матрицами одинаковой размерности и выполняются над каждым из элементов. Используя логические операции И, ИЛИ, НЕ, можно создавать разнообразные составные условия. Например, можно сделать проверку, что переменная x попадает в диапазон от -5 до 5, но не принадлежит диапазону от 0 до 1. 11

>>x=1;

>> x >= -5 & x <= 5 & (x < 0 | x > 1) ans =

0

>>x = -3;

>> x >= -5 & x <= 5 & (x < 0 | x > 1) ans =

1

В составном условии использованы круглые скобки. Дело в том, что приоритет операции И выше приоритета операции ИЛИ, и если бы не было круглых скобок, то порядок действий в выражении был бы другой. Выражение выглядело бы так: x >= -5 и x <= 5 и x < 0 или x > 1. Сначала выполнится операция И, затем ИЛИ. Очевидно, что получился бы другой результат.

Круглые скобки в выражении используются для изменения порядка выполнения операций.

Приоритет элементарных операций в ML

Пока перечислим приоритеты операций над числовыми данными. Приоритет операций определяет порядок действий в выражении. Его можно изменять с помощью круглых скобок. Далее представлены операции в порядке убывания приоритета:

1)логическая операция НЕ ( );

2)возведение в степень( ^);

3)унарный плюс (+), унарный минус (-);

4)умножение и деление( *, /);

5)сложение и вычитание (+, -);

6)операции отношения (, <=, >=, ==, =);

7)логическая операция И (&);

8)логическая операция ИЛИ (|).

Основные математические функции MatLab

ML существует большое количество элементарных математических функций для

логарифмические, экспоненциальные и функции округления. Каждая функция

обладает именем и списком аргументов, которые задаются в круглых скобках и,

если их несколько, перечисляются через запятую.

9

Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква d. sin(x) – аргумент в радианах, а sind(x) – аргумент в градусах.

Некоторые часто используемые математические функции:

exp(x) –экспонента числа x;

log(x) – натуральный логарифм;

log10(x) – десятичный логарифм;

sqrt(x) – квадратный корень;

abs(x) – абсолютное значение x;

mod(x, y) – остаток от целочисленного деления с учетом знака;

rem(x, y) – остаток от целочисленного деления без учета знака;

real(z) – вещественная часть комплексного числа;

imag(z) – мнимая часть комплексного числа;

round(x) – округление до ближайшего целого.

Более полный список основных математических функций MatLab:

10

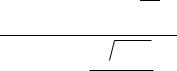
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения:

3cos 2 x3 sin(x )

Вычислить: res= 3 .106 ln/ y/ e x 1

2x

Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. Причем открытую скобку следует сразу закрывать и продолжать набор формулы внутри скобок. В этом случае число открывающих скобок будет равно числу закрывающих, и вероятность ошибки будет минимальной.

Если в выражении многократно встречаются одинаковые фрагменты, то их целесообразно вычислять 1 раз и результат помещать в отдельные переменные.

Это позволяет избежать одинаковых вычислений и тем самым оптимизирует вычисления.

x=0.5;

y=1;

res=(3*cos(x^3)^2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6 res =

11