Чтобы отменить разделение для построения графика во весь экран,

необходимо задать команду: Subplot(1, 1, 1).

Команда Subplot(3, 3, 1) открывает окно с 9 подокнами и текущее окно -1.

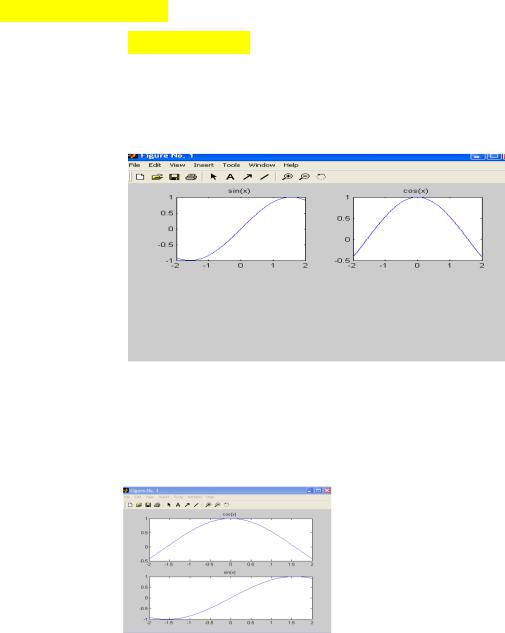
Разделим экран на четыре части. В окнах 1 и 2 выведем графики функций cos(x) и sin(x) соответственно.

>>x = -2: 0.01: 2;

>>f1 = sin(x); >>subplot(2, 2, 1);

>>plot(x, f1); >>title('sin(x) '); >>y2 = cos(x); >>subplot(2, 2, 2); >>plot(x, y2); >>title('cos(x) ');

Разделим экран на две части по вертикали :

>>subplot(2,1,1)

>>plot(x,y2) >>title('cos(x) '); >>subplot(2,1,2) >>plot(x,f1) >>title('sin(x) ');

Изменение масштаба графика

При построении графиков система ML автоматически выбирает масштаб, чтобы в поле графика разместить все вычисленные значения. Но можно самостоятельно задать масштаб и управлять осями, которые располагаются на экране.

Для этого используются следующие команды: axis off – убрать с экрана;

axis on – вернуть на экран.

73

Можно установить свой масштаб по осям:

axis([xmin xmax ymin ymax]),

где xmin, xmax – минимальное и максимальное значения по оси x; ymin, ymax – минимальное имаксимальное значения по оси y.

Eсли график трехмерный, то команда будет иметь вид: axis([xmin xmax ymin ymax zmin zmax]).

axis ('i j’) – центр координат

будет расположен в левом верхнем углу экрана

axis (‘xy’) – обычное расположение

осей

axis (‘square’) – график будет занимать область с одинаковыми

диапазонами значений по осям х и у.

axis (‘equal’) – одинаковый масштаб по обеим осям.

axis (‘auto’) – устанавливает (возвращает) масштаб по умолчанию.

Мы строили графики функций в одних осях и в одинаковом масштабе. Иногда требуется построить графики 2-х функций, значения которых очень отличаются друг от друга. При использовании одинакового масштаба, мы рискуем одну из функций не увидеть. Чтобы увидеть обе функции на графике, надо иметь разный масштаб по осям. Тогда надо воспользоваться командой plotyy.

>>B=0.5:0.001:3;

>>f1=B.^-3;

>>f2=1000*(B+0.5);

>>plotyy(B,f1,B,f2)

74

В этом случае справа обозначается еще одна ось с отметками на оси для другой функции. Цвет новой оси y и графика этой функции выводится в одном цвете. Если такой вариант неудобен, то можно построить графики в разных окнах.

Можно построенные графики прикрепить к командному окну, чтобы оно было перед глазами. Для этого надо щелкнуть по кнопке с черной стрелкой (Dock Figure) в правом углу графического окна.

Диаграммы

Диаграммы позволяют представить векторные и матричные данные в наглядной форме. В системе легко можно построить различного вида круговые pie(<вектор>) и с столбиковые bar(<вектор>) диаграммы.

Иногда столбиковые диаграммы используют для закраски области под графиком bar(x,y). В последних версиях Матлаба для этой цели существует функция area(x,y).

Трехмерные графики

Система ML имеет возможности для создания трехмерных графиков.

График поверхности (трехмерный график) – это график, положение точки в котором определяется значениями трех координат M(x,y,z). Три плоскости XY, XZ, YZ называются координатными плоскостями.

Процесс построения графика двух переменных включает такие же этапы, что и построение графика функции одной переменной: задание

маcсивов значений аргумента; формирование матрицы значений

функции;

вызов специальной функции для построения графика; при необходимости отображение заголовков и других атрибутов.

Трехмерным аналогом функции plot является функция plot3, которая позволяет создавать трехмерные линии.

1

Команда plot3 относится к функции двух переменных z(x,у). Она строит аксонометрическое изображение трехмерных объектов.

plot3(x, y, z)– строит массив точек, представленных векторами х, y и z, соединяя их отрезкамипрямых.

Если есть три вектора x, y, z, задающих координаты точек в трехмерном пространстве, то при выполнении функции plot3(x,y,z),

построится проекция трехмернойлинии.

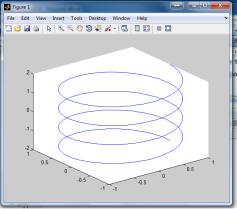
Пусть требуется построить спираль, которая вычисляется по форму-

лам: x=cos(2*pi*t), y=sin(2*pi*t), t принадлежит интервалу t=[-2 2].

Сначала зададим вектор значений аргумента t, создадим вектора ко-

ординат Х и У, а затем используем команду plot3.

Запишем:

Т=-2:0.01:2; % задали вектор значений аргумента

% можно создать вектор x и вектор y отдельной командой, а можно записать формулу прямо в команде plot3:

X= cos(2*pi*Т);

Y= sin(2*pi*T); plot3(X, Y, T

);

или

заданы формулами

Ось Z направлена вверх, X – вправо, Y - влево

2