- •Мiнiстерство освiти і науки україни національний технічний університет
- •Стержньових систем методом сил”
- •Енергетичні методи визначення переміщень в стержньових системах
- •Інтеграл Максвелла – Мора
- •Обчислення інтегралів Мора способом перемноження епюр (способом Верещагіна).
- •Перемноження епюр за правилами трапецій і Сімпсона – Карнаухова.
- •Приклади визначення переміщень.
- •Статично невизначувані системи
- •Основні поняття та визначення
- •Метод сил
- •Канонічні рівняння методу сил
- •Використання властивостей симетрії при виборі основної статично визначуваної системи
- •Перевірка правильності розрахунків
- •Приклади розкриття статичної невизначуваності
- •Розрахунково – проектувальне завдання
- •Задача 1. Визначення внутрішніх зусиль у статично невизначуваних балках
- •Чисельні дані до задачі №1.
- •Задача 2. Визначення внутрішніх зусиль у статично невизначуваних рамах
- •Чисельні дані до задачі №2
- •Задача 3. Визначення внутрішніх зусиль в статично невизначуваних плоскопросторових рамах та визначення розмірів поперечного перерізу
- •Чисельні дані до задачі 3
- •Типи перерізів до задачі 3
- •Контрольна задача № 4. (Для самостійної роботи)
- •Контрольна задача № 5. (Для самостійної роботи)
- •Чисельні дані для контрольних задач №4, №5
- •Зразок виконання розрахунку статично невизначуваної балки
- •Зразок виконання розрахунку статично невизначуваної рами
- •Зразок виконання розрахунку статично навизначуваної плоскопросторової рами
Обчислення інтегралів Мора способом перемноження епюр (способом Верещагіна).
Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр прямолінійна. Ця умова виконується для систем, що складаються з прямих стержнів, оскільки при цьому епюри внутрішніх сил від одиничного навантаження (зосередженої сили або пари) завжди обмежені прямими лініями.
Обчислимо
інтеграл
![]() для випадку, коли
для випадку, коли![]() епюра від заданого навантаження має
довільну форму, а від одиничного –
прямолінійна (рис. 2).
епюра від заданого навантаження має
довільну форму, а від одиничного –
прямолінійна (рис. 2).
|
|
Позначимо
через
|
Інтеграл
у правій частині рівняння є статичним
моментом площі епюри
![]() відносно осіО-О:
відносно осіО-О:
![]()
де
![]() – абсциса центра ваги епюри
– абсциса центра ваги епюри![]() .
.
Тоді
![]() ,
оскільки
,
оскільки![]() .
.
Отже,
інтеграл Мора дорівнює добутку площі
епюри від зовнішнього навантаження
![]() на ординату одиничної епюри
на ординату одиничної епюри![]() ,
розташованої під центром ваги епюри
від заданого зовнішнього навантаження.
Загальна формула (1.3) для визначення
переміщень у системах з прямих стержнів
набирає вигляду:
,
розташованої під центром ваги епюри
від заданого зовнішнього навантаження.
Загальна формула (1.3) для визначення
переміщень у системах з прямих стержнів
набирає вигляду:
![]() (1.7)
(1.7)
Графоаналітичний спосіб визначення інтеграла Мора був запропонований О.М.Верещагіним і має назву способу Верещагіна. Обчислення за цією формулою виконують по ділянках, на кожній з яких епюра від одиничного навантаження повинна бути прямолінійною. Тоді, коли обидві епюри прямолінійні, можна множити площу будь-якої з них на ординату іншої під центром ваги першої.
Якщо
епюра
![]() має складний вигляд, то її слід розбити
на прості фігури, для яких легко визначити
площу і положення центра ваги. При цьому
кожну з площ треба множити на ординату
одиничної епюри під центром ваги
відповідної площі. Ординати в цьому
разі зручно позначати замість
має складний вигляд, то її слід розбити
на прості фігури, для яких легко визначити
площу і положення центра ваги. При цьому
кожну з площ треба множити на ординату
одиничної епюри під центром ваги
відповідної площі. Ординати в цьому
разі зручно позначати замість![]() літерами
літерами![]() ,
де
,
де![]() .
.
Отже,
![]() (1.8)
(1.8)
Користуючись
способом Верещагіна, необхідно пам'ятати,
що добуток епюр позитивний, якщо ординати
обох епюр відкладені з одного боку від
осі стержня рами, і негативний, якщо
ординати епюр відкладені з різних
сторін. В тих випадках, коли одна з епюр
криволінійна, береться площа
![]() криволінійної епюри, а ордината
криволінійної епюри, а ордината![]() під центром ваги з прямолінійної епюри.
При цьому треба враховувати правило
знаків: Якщо
епюри, що перемножуються, лежать по одну
сторону (обидві нагорі або внизу),
добуток позитивний; якщо епюри, що
перемножуються, лежать по різні сторони
- добуток негативний.
Якщо
одна або обидві епюри перетинають в
межах дільниці нульову ось, то слідує
перемножувати епюри по частинам.
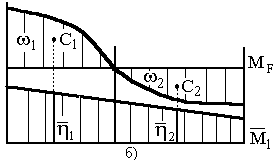
Особливості
застосування правила Верещагіна видно
з рис. 3а,б.
під центром ваги з прямолінійної епюри.
При цьому треба враховувати правило
знаків: Якщо
епюри, що перемножуються, лежать по одну
сторону (обидві нагорі або внизу),
добуток позитивний; якщо епюри, що
перемножуються, лежать по різні сторони
- добуток негативний.
Якщо
одна або обидві епюри перетинають в
межах дільниці нульову ось, то слідує
перемножувати епюри по частинам.
Особливості
застосування правила Верещагіна видно
з рис. 3а,б.
|
|
|
|
|
|
Рис. 3
Переміщення від дії осьових і поперечних сил, а також крутних моментів виражаються аналогічно:
![]()
![]() (1.9)
(1.9)
![]()
де
![]() - площа епюри
- площа епюри![]() ,
,![]() - площа епюри
- площа епюри![]() ,
,![]() - площа епюри
- площа епюри![]() від заданого навантаження;
від заданого навантаження;![]() - ординати відповідних епюр осьових,
поперечних сил і крутних моментів від
одиничного навантаження, взяті під
центрами ваги епюр
- ординати відповідних епюр осьових,
поперечних сил і крутних моментів від
одиничного навантаження, взяті під
центрами ваги епюр![]() ,
,![]() ,
,![]() .
.
Зазначимо,
що епюри внутрішніх силових факторів
від зовнішнього та одиничного навантажень
на окремих ділянках стержня складаються
з досить простих фігур: прямокутник,
трикутник, парабола і т.д. Тоді для
використання способу Верещагіна (1.8),
(1.9) необхідно визначити площу
![]() та координату центра ваги
та координату центра ваги![]() цих простих фігур:
цих простих фігур:
Таблиця 1
|
Трикутник |
Трикутник |
|
|
|
|
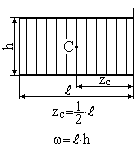
Прямокутник |
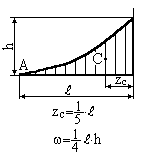
Парабола (квадратна) з вершиною в т. А |
|
|
|
|
Парабола (квадратна) з вершиною в т.А |
Парабола (кубічна) з вершиною в т.А |
|
|
|
Продовження таблиці 1
|
Парабола (квадратна) з вершиною в т.А |
Парабола (кубічна) з вершиною в т.А |
|
|
|