58. Измерение связей между социально-экономическими явлениями – важнейшая задача статистики. Формы и виды взаимосвязей.
Особенности статистического изучения связи между соц.-эк. явлениями заключаются в том, что они представл. возможность не только выявить наличие и направл. связи, но и количественно ее оценить и выразить аналитически. Связи между явл. и их признаками в статистике классифицируют по ряду оснований.
Признаки по характеру их роли во взаимосвязи подразделяют на факторные (х) и результативные (у). Факторные признаки обусловливают изменение других, связанных с ними признаков. Признаки, изменяющиеся под действием факторных, называются результативными.
По степени тесноты связи между явлениями и их признаками подразделяют на полные, или функциональные, и неполные, корреляционные, или статистические. Полные (функциональные) - связи, при которых определенным значениям фактор. признаков соотв. строго опред. знач. результативных; в неполных (корреляционных, статистических) связях одним и тем же знач. фактор. признаков могут соотв. разные значения результативных.
По направлению выделяют связь прямую и обратную. Прямая —связь, при которой оба вида признаков (фактор. и результ.) изменяются в одном и том же направл.. В случае же обратной связи значения результ. признаков изменяются под действием фактор., но в противополож. направл. по сравнению с изменением фактор. признаков.
По аналитическому выражению выделяют прямолинейные (линейные) и нелинейные связи. Если стат. связь явлений может быть приближенно выражена мат. ур-ем прямой линии, то ее называют прямолинейной (линейной) связью, если же она может быть выражена ур-ем кривой, то — нелинейной (криволинейной).
59. Статистические методы изучения связей: метод сравнения параллельных рядов, метод аналитических группировок, графический метод, балансовый метод.
Для выявления связи, ее характера, направления в статистике используются следующие методы:
метод приведения параллельных данных: приводятся два ряда данных о двух явлениях или двух признаках, связь между которыми необходимо выявить; по характеру изменений делают заключения о наличии или об отсутствии;
балансовый характер. зависимость между источниками формир. ресурсов ( пассивов) и их использ. (активов);
метод аналитических группировок начинается с построения макета таблицы. В подлеж. таблицы содерж. группировка по фактор-признаку, в сказуемом – исход. данные для исчисл. средних результ. признака. Согласованность в колеблемости факторного и результ. признаков обусл. налич. связи между ними.
графический — используя данные об индивид. знач-х признака-фактора и соотв. ему значениях результат. признака, можно построить в прямоуг. коорд. точечный график, называемый «полем корреляции». При граф. методе строится корреляц. поле зависимости результ. признака (у) и факторного (х).
60. Понятие прямолинейной корреляции. Нахождение параметров уравнения регрессии, оценка тесноты связи при прямолинейной зависимости.
Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии f(x) и φ(x) являются линейными. В этом случае обе линии регрессии являются прямыми; они называется прямыми регрессии. Уравнение линейной корреляции имеет вид:
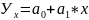
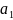показывает,
на сколько измен. результатив. признак,
если факторный возрастет на единицу.
Параметры:
;
.
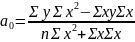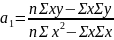Для оценки тесноты линейных корреляционных зависимостей между величинами Х и Y по результатам выборочных наблюдений вводится понятие выборочного коэффициента линейной корреляции (Пирсона), определяемого формулой:
