3.1. Распределение зарядов на проводнике.

Электрические заряды, сообщённые проводнику извне, в состоянии равновесия распределяются так, что электрическое поле внутри проводника отсутствует

.

Э то вытекает из закона сохранения энергии. Если бы выполнялось условие Е ≠ 0, то в проводнике протекал бы ток без дополнительных источников энергии. Избыточные заряды, сообщенные проводнику в состоянии равновесия, распределяются только по внешней поверхности проводника (рис. 40). Из условия равновесия зарядов следует, что потенциал всех точек проводника как внутри, так и на поверхности одинаков. Это ясно из условия Е=0; так как  , то φ=const.

Та ким образом, в условиях равновесия зарядов и поверхность, и объем проводника являются эквипотенциальными.

Е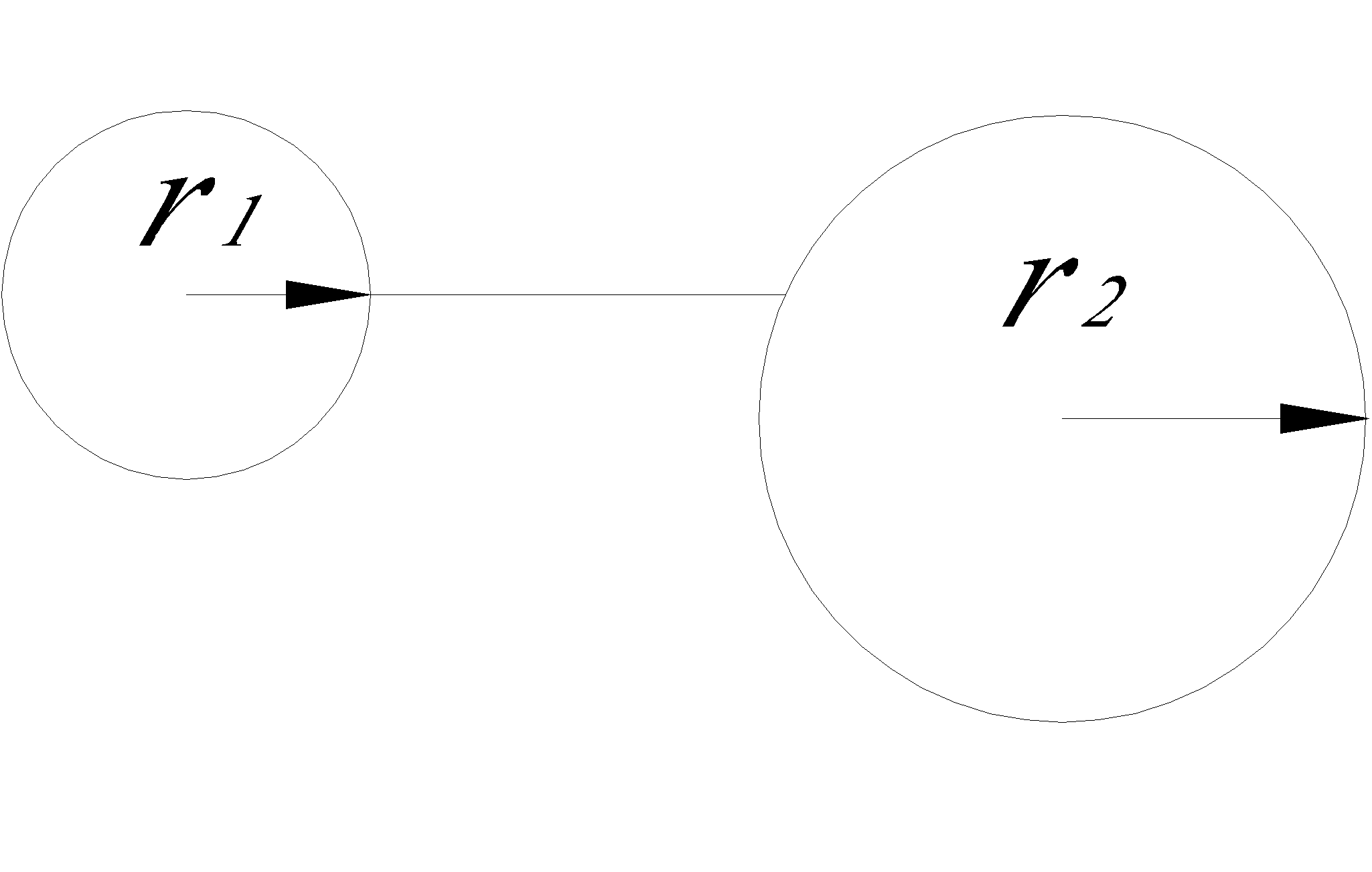 сли заряды находятся в равновесии, то в любой точке проводника вектор  перпендикулярен поверхности, то есть   и  =0. действительно, если бы ≠ 0, то это вызвало бы движение зарядов по поверхности проводника и равновесие отсутствовало бы.

Электрическая емкость уединенного проводника

Уединенным называется проводник, вблизи которого нет других заряжен­ных тел, диэлектриков, которые могли бы повлиять на распределение зарядов дан­ного проводника.

Отношение величины заряда к потенциалу для конкретного проводника есть величина постоянная, называемая электроемкостью (емкостью) С , .

Таким образом, электроемкость уединенного проводника численно равна заряду, который необходимо сообщить проводнику, чтобы изменить его потен­циал на единицу. Опыт показал, что электроемкость уединенного проводника зависит от его гео­метрических размеров, формы, диэлектрических свойств окружающей среды и не за­висит от величины заряда проводника.

Рассмотрим уединенный шар радиуса R, находящийся в однородной среде с диэлектрической проницаемостью . Ранее было получено, что потенциал шара ра­вен  . Тогда емкость шара , т.е. зависит только от его ра­диуса.

За единицу емкости принимается 1фарад (Ф). 1Ф - емкость такого уединенно­го проводника, потенциал которого изменится на 1В при сообщении заряда 1Кл. Фарад - очень большая величина, поэтому на практике используют дольные едини­цы : милли­фарад (мФ, 1мФ=10^-3Ф), микрофарад (мкФ, 1мкФ=10^-6Ф), нанофарад (нФ, 1нФ=10^-9Ф), пикофарад (пФ, 1пФ=10^-12Ф).

Уединенные проводники даже очень больших размеров обладают малыми ем­костями. Емкостью в 1Ф обладал бы уединенный шар радиуса, в 1500 раз большего радиуса Земли. Электроемкость Земли составляет 0.7 мФ

Ёмкость цилиндрического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), один вставлен в другой, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками, так же пренебрегаем краевыми эффектами. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l. При наличии диэлектрика между обкладками разность потенциалов

Подставим в формулу электроемкости конденсатора и у нас получится формула для цилиндрического конденсатора:

 

Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:

Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть  , а следовательно можно считать, что   емкость сферического конденсатора будет равна  . Площадь сферы   следовательно формула будет совпадать с формулой емкости плоского конденсатора 

1. Рассмотрим систему, состоящую из двух проводников, заряды которых численно равны, но противоположны по знаку. Обозначим разность потенциалов проводников1-2 а абсолютное значение их зарядов q. Если проводники находятся вдали от каких бы то ни было заряженных тел и иных проводников, то, как показывают и теория и эксперименты, разность потенциалов 1-2 пропорциональна заряду q, т. е. 1-2=q/C. Скалярная величина С, равная абсолютному значению отношения электрического заряда одного проводника к разности электрических потенциалов двух проводников при условии, что эти проводники имеют одинаковые по модулю, но противоположные по знаку заряды и что все другие проводники бесконечно удалены, называется взаимной электрической емкостью двух проводников (электрической емкостью между двумя про­водниками):

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 1.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рис. 1.6.2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля (см. § 1.4).

Рисунок 1.6.1. Поле плоского конденсатора

Рисунок 1.6.2. Идеализированное представление поля плоского конденсатора. Такое поле не обладает свойством потенциальности

Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением

Согласно принципу суперпозиции, напряженность   поля, создаваемого обеими пластинами, равна сумме напряженностей   и   полей каждой из пластин: 

Внутри конденсатора вектора   и   параллельны; поэтому модуль напряженности суммарного поля равен 

Вне пластин вектора   и   направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора: 

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз: 

Сферический и цилиндрический конденсатор.

Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R₁ и R₂. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R₁ и R₂ и длины L. Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами: 

(сферический конденсатор),   (цилиндрический конденсатор).

Параллельное и последовательное соединение конденсаторов.

Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.6.3) напряжения на конденсаторах одинаковы: U₁ = U₂ = U, а заряды равны q₁ = С₁U и q₂ = C₂U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q₁ + q₂ при напряжении между обкладками равном U. Отсюда следует 

Таким образом, при параллельном соединении электроемкости складываются.

Рисунок 1.6.3. Параллельное соединение конденсаторов. C = C1 + C2

Рисунок 1.6.4. Последовательное соединениеконденсаторов.

При последовательном соединении (рис. 1.6.4) одинаковыми оказываются заряды обоих конденсаторов: q₁ = q₂ = q, а напряжения на них равны   и   Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U₁ + U₂. Следовательно, 

При последовательном соединении конденсаторов складываются обратные величины емкостей.

Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.

Энергия системы зарядов, уединенного проводника, конденсатора.

1. Энергия системы неподвижных точечных зарядов. Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q₁ и Q₂, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):     где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно,    и    поэтому W₁ = W₂ = W и    Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна    (1)  где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го.  2. Энергия заряженного уединенного проводника. Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна   ");?>" alt="элементарная работа сил электрического поля заряженного проводника">  Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу    (2)  Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:    (3)  Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем     где Q=∑Q_i - заряд проводника.  3. Энергия заряженного конденсатора. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна   (4)  где Q — заряд конденсатора, С — его емкость, Δφ — разность потенциалов между обкладками конденсатора.  Используя выражение (4), будем искать механическую (пондеромоторную) силу, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = — dW, откуда    (5)  Подставив в (4) выражение для емкости плоского конденсатора, получим    (6)  Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу:    где знак минус указывает, что сила F является силой притяжения.  4. Энергия электростатического поля. Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε₀εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда    (7)  где V= Sd — объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е.  Объемная плотность энергии электростатического поля (энергия единицы объема)    (8)  Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε₀Е.  Формулы (4) и (7) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля. Возникает вопрос о локализации электростатической энергии и что является ее носителем — заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика занимается изучением постоянных во времени поля неподвижных зарядов, т. е. в ней поля и попродившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на данный вопрос не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать отдельно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, которые способны переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле. 

Сегнетоэлектриками называют вещества, обладающие спонтанной поляризацией, направление которой может быть изменено с помощью внешнего электрического поля. Сегнетоэлектрики имеют доменную структуру. Домены представляют собой макроскопические области, обладающие спонтанной (самопроизвольной) поляризацией. Линейные размеры доменов составляют от 1 мкм до 1 мм. Направление электрических моментов у разных доменов различно, поэтому суммарная поляризованность материала может быть равна нулю.

Внешнее электрическое поле изменяет направления электрических моментов доменов, что создает эффект очень сильной поляризации. Доменная поляризация связана с процессами зарождения и роста новых доменов за счет смещения доменных границ, которые в итоге вызывают переориентацию вектора спонтанной поляризованности в направлении внешнего электрического поля. Следствием этого является нелинейная зависимость электрической индукции от напряженности поля (рис.8.1). При изменении направления поля кривая описывает гистерезисную петлю. Точки В и С определяют состояние технического насыщения, Е_с коэрцитивная сила,D_r остаточная электрическая индукция. Площадь гистерезисной петли пропорциональна энергии, рассеиваемой в диэлектрике за один период. Совокупность вершин гистерезисных петель, полученных при различных значениях амплитуды переменного поля, образует основную кривую поляризации сегнетоэлектрика.

Специфичные свойства сегнетоэлектриков проявляются лишь в определенном диапазоне температур. В процессе нагревания выше некоторой температуры происходит распад доменной структуры, и сегнетоэлектрик переходит в параэлектрическое состояние. Температура такого фазового перехода получила название сегнетоэлектрической точки Кюри (Т_к).

По типу химической связи и физическим свойствам все сегнетоэлектрики подразделяют на 2 вида: ионные и дипольные кристаллы. У первой группы характерным структурным элементом является кислородный октаэдр, благодаря чему эти материалы получили название сегнетоэлектриков кислородно-октаэдрического типа. К ним относятся: титанат бария (BaTiO₃), титанат свинца (PbTiO₃), ниобат калия (KNbO₃), ниобат лития (LiNbO₃), танталат лития (LiTaO₃), йодат калия(KJO₃), барий-натриевый ниобат или сокращенно БАНАН (Ba₂NaNb₅O₁₅) и др.

У дипольных сегнетоэлектриков имеются готовые полярные группы атомов, способные занимать различные положения равновесия. К ним относятся: сегнетова соль (NaKC₄H₄O₆4H₂O), триглицинсульфат ((NH₂CH₂COOH)₃H₂SO₄), дигидрофосфат натрия (KH₂PO₄), нитрат натрия (NaNO₂) и др.

Б

Рис.8.2. Идеальная форма кристалла кварца и его главные оси. а-левый кварц б-правый кварц

ольшинство сегнетоэлектриков первой группы имеют значительно более высокую Т_к и большее значение спонтанной поляризованности, чем сегнетоэлектрики второй группы.

1. Возникновение самопроизвольной поляризации в пределах одной элементарной ячейки кристалла вызовет возникновение электрического поля в соседних ячейках. Под воздействием этого энергетически более выгодной становится поляризация соседних ячеек с параллельно ориентированными электрическим моментами. Вследствие этого образуется область в кристалле с параллельно ориентированными электрическими моментами элементарных ячеек – домен.

2. К

Рис. 7

ристаллу энергетически более выгодно находиться в многодоменном состоянии, т.к. в окружающем пространстве в этом случае создается меньшее электрическое поле с энергией  (гдеV₀– объем окружающего пространства, где создается энергетическое поле). Этот факт иллюстрирует рис.7. Другой причиной многодоменного состояния кристалла является случайность процесса самоорганизации по отношению к возможным направлениям поляризации.

3. Взаимное расположение векторов поляризованности доменов не является хаотичным.

В

Рис. 8

кристаллах титаната бария смещение ионов происходит в направлении ребер исходной кубической ячейки. Поэтому существует шесть возможных направлений спонтанной поляризации – по два взаимно противоположных направления вдоль ребер кубической ячейки. Отсюда вытекает взаимная направленность электрических моментов доменов – домены ориентированы под углами 90⁰С и 180⁰С. Рис.8 иллюстрирует схему расположения доменов в кристалле титаната бария. В поликристаллических образцах по причине хаотичности монокристаллических блоков хаотичны и направления электрических моментов доменов.

4. По ляризация образца во внешнем электрическом поле проходит несколько стадий. При малых внешних полях (областьIна рис.9) происходит обратимое смещение границ доменов. Домены, энергия которых меньше во внешнем поле ( ), т.е.  , увеличиваются, а домены с  - уменьшаются.

В

Рис. 9

областиIIпроисходит необратимое скачкообразное смещение границ доменов. К концу областиIIостаются только домены с энергетически выгодной ориентацией электрических моментов во внешнем поле.

В области IIIнаблюдается процесс поворота электрических моментов доменов по направлению электрического поля.

Область IVсоответствует насыщению, когда электрические моменты доменов ориентированы по направлению внешнего поля.

5. При уменьшении электрического поля после достижения насыщения должен был бы возникать обратный процесс. Но это оказывается невозможным. Дезориентация доменов связана с образованием доменов с новыми направлениями поляризованности за счет энергии теплового движения и последующим их ростом. Вероятность этого процесса невелика и определяется

Поэтому наблюдается запаздывание изменения поляризованности кристалла при уменьшении внешнего электрического поля, т.е. возникает гистерезис. Для достижения состояния с Р=0 необходимо создание внешнего поля, способствующего дезориентационному процессу и равного коэрцитивной силе.

Гистерезис (от греч. hysteresis - отставание, запаздывание) , явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность) , неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля) . Гистерезис наблюдается в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. Неоднозначная зависимость величин наблюдается в любых процессах, т. к. для изменения состояния тела всегда требуется определённое время (время релаксации) и реакция тела отстаёт от вызывающих её причин. Такое отставание тем меньше, чем медленнее изменяются внешние условия Однако для некоторых процессов отставание при замедлении изменения внешних условий не уменьшается. В этих случаях неоднозначную зависимость величин называется гистерезисной, а само явление – Гистерезис

Электрическим током называется направленное (упорядоченное) движение электрических зарядов (рис.13.1). Сами эти частицы называются носителями тока.

Ток может идти в твёрдых телах, жидкостях и газах. Если среда является проводником с большим количеством свободных электронов, то течение электрического тока осуществляется за счёт дрейфа этих электронов. Дрейф электронов в проводниках, не связанный с перемещением вещества, называют током проводимости. К току проводимости относится упорядоченное движение электронов в проводниках, ионов в электролитах, электронов и дырок в полупроводниках, ионов и электронов в газах. Упорядоченное перемещение электрических зарядов, связанное с перемещением в пространстве заряженного тела, называют конвекционным током.

За направление тока принят дрейф положительных зарядов (электроны проводимости всегда движутся в направлении, противоположном направлению тока (от «+» к «-»)). Это может показаться неудобным, но зато теперь не нужно различать направление тока в проводнике и электростатического поля, вызывающего этот ток: эти направления всегда совпадают.

С ила тока – скалярная величина, равная отношению количества электричества dq, которое за время dt переносится через данное сечение проводника, ко времени dt:

(13.1)

Постоянным током называют электрический ток, сила и направление которого с течением времени не изменяются. Для постоянного тока

где q - электрический заряд, проходящий за время t через поперечное сечение проводника.

Единица силы тока – ампер (А).

Определим скорость, с которой осуществляется дрейф электронов в проводнике с током.

Путь за время Δt через сечение проводника S прошло N электронов с суммарным зарядом Δq = Nе. Если скорость направленного движения электронов равна υ, то за время Δt все они окажутся в пределах участка длиной ℓ = υ Δt и объёмом V=Sℓ. Таким образом,

(13.2)

выразив здесь число носителей тока через их концентрацию (N = nV= nSℓ)

Отношение силы тока І к площади поперечного сечения проводника S, перпендикулярного направленню тока – есть векторная величинаназываемая плотностью тока.

(13.3)

Тогда скорость электронов в проводнике можно записать  , отсюда

Плотность тока может быть вычислена по формуле

j = ne‹υ› (13.4)

Таким образом, плотность тока в проводнике пропорциональна концентрации свободных электронов в нём и скорости их движения.

Вектор j направлен вдоль направления тока, т.е. совпадает с направлением упорядоченного движения положительных зарядов.

Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т.е.

(13.5)

где dS = n∙dS (n = единичный вектор нормали к площадке dS, составляющей с вектором j угол α ).

Электрическое поле постоянного тока называется стационарным. В отличии от электростатического поля стационарное электрическое поле создаётся движущимися зарядами. Однако распределение этих зарядов в проводнике с постоянным током не меняется со временем: на место уходящих электрических зарядов непрерывно приходят новые. Поэтому электрическое поле, создаваемое этими зарядами, оказывается почти таким же, как и поле неподвижных зарядов.

Отличаются же они тем, что электростатическое поле внутри проводника отсутствует, в то время как стационарное поле постоянных токов существует и внутри проводников (иначе по ним не шёл бы ток).

Если в проводнике создать электрическое поле и не принять мер для его поддержания, то, как было уже установлено, перемещение носителей заряда приведет очень быстро к тому, что поле внутри проводника исчезнет и, следовательно, ток прекратиться. Для того чтобы поддерживать ток достаточно долго, нужно от конца проводника с меньшим потенциалом (носители тока предполагаются положительными) непрерывно отводить приносимые сюда заряды, а к концу с большим потенциалом непрерывно их подводить. Т.е. необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути (13.2). Циркуляция вектора напряженности электростатического поля, как известно равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания потенциала, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания потенциала, т.е. против сил электростатического поля. Перемещение, зарядов на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами.

Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных, веществ, электрическими (но не электростатическими) полями, порожденными меняющимися во времени магнитными полями и т.д.

Например, в гальванических элементах и аккумуляторах происхождение сторонних сил – химическое. В генераторах электрического тока сторонние силы – это силы Лоренца, действующие со стороны магнитного поля.

Устройства, обеспечивающие возникновение и действие сторонних сил, называют источниками тока. В этих устройствах происходит разделение разноимённых зарядов. Под действием сторонних сил электрические заряды внутри источника тока движутся в направлении, противоположном действию сил электрического поля. В результате этого на полюсах источника тока поддерживается постоянная разность потенциалов.

Подобно тому, как насос сообщает энергию воде, поднимая её вверх, источник тока сообщает энергию заряженным частицам. Как для работы насоса, поднимающего воду, так и для работы источника тока необходима энергия. В зависимости от типа источника тока, в нём происходит преобразование механической, внутренней или ещё какой-либо энергии в электрическую. В зависимости от вида энергии, которая внутри источника тока преобразуется в электрическую энергию, различают механические, химические, тепловые источники тока.

Сторонние силы совершают работу по перемещению электрических зарядов.

Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (э.д.с.) ε, действующей в цепи.

Сторонняя сила F_ст, действующая на заряд q₀, может быть выражена как

F_ст = E_ст q₀,

где E_ст – напряжённость поля сторонних сил. Работа же сторонних сил по перемещению заряда q₀ на замкнутом участке цепи равна

(13.6)

Разделив на q₀, получим выражение для э.д.с., действующей в цепи:

(13.7)

т.е. эдс, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряжённости поля сторонних сил. ЭДС, действующая на участке 1-2, равна

Н а заряд q₀ помимо сторонних сил действует также силы электростатического поля F_э = E q₀. Таким образом, результирующая сила, действующая в цепи на заряд q₀, равна

F =F_ст + F_э = q₀(Е_ст + E_э) (13.8)

Рисунок – 13.3

Работа, совершаемая результирующей силой над зарядом q₀ на участке 1-2, равна

(13.9)

Используя выражения   и  , можем записать

А₁₂ = q₀ε₁₂ + q₀ (φ₁-φ₂) (13.10)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в данном случае А₁₂ = q₀ε₁₂

Напряжением U на участке 1-2 называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении положительного единичного заряда на данном участке цепи.

U₁₂ = ε₁₂ + (φ₁-φ₂) (13.11)