
Типовые
.pdf41
Задача 31. Используя формулу Пуассона, найти решения задачи Коши для уравнения теплопроводности.
31.1ut=uxx
ut=0= e− x 2 + x
31.4ut=4uxx
u t=0= e− 2x 2 + x
31.7ut=7uxx
u t=0= e− 2x 2 + 2x
31.10 ut=10uxx
u t=0= e− 2x 2 − 2x
31.13 ut=13uxx
u t=0= e−3x 2 + 2x
31.16 ut=16uxx
u t=0= e− 4x 2 − 2x
31.19 ut=13uxx
u t=0= e− 2x 2 + 4x
31.22 ut=10uxx
u t=0= e− 2x 2 − 4x
31.25 ut=7uxx
u t=0= e− 4x 2 + 2x
31.28ut=4uxx
u t=0= e−3x 2 + 6x
31.31ut=uxx
u t=0= e− 4x 2 − 4x .
31.2ut=2uxx
u t=0= e− x 2
31.5ut=5uxx
u t=0= e− 2x 2 − x
31.8ut=8uxx
u t=0= e−3x 2
31.11 ut=11uxx
u t=0= e−3x 2 − x
31.14 ut=14uxx
u t=0= e− 4x 2 + x
31.17 ut=15uxx
u t=0= e− x 2 + 2x
31.20 ut=12uxx
u t=0= e− x 2 − 2x
31.23 ut=9uxx
u t=0= e− x 2 + 4x
31.26 ut=6uxx
u t=0= e− 4x 2 − x
31.29ut=3uxx
u t=0= e− 4x 2 −6x
31.3ut=3uxx
u t=0= e− 2x 2
31.6 ut=6uxx u t=0= e− x 2 − x
31.9ut=9uxx
u t=0= e−3x 2 + x
31.12 ut=12uxx u t=0= e− 4x 2
31.15 ut=15uxx u t=0= e−3x 2 − 2x
31.18 ut=14uxx u t=0= e−3x 2 +3x
31.21 ut=11uxx u t=0= e−3x 2 −3x
31.24 ut=8uxx u t=0= e− x 2 − 4x
31.27 ut=5uxx u t=0= e−3x 2 −6x
31.30 ut=2uxx u t=0= e− 4x 2 +8x

42
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. Найти в указанной области отличные от тождественного нуля решения y=y(x) дифференциального уравнения, удовлетворяющие заданным краевым условиям (задача Штурма-Лиувилля).
y"(x) + λy(x) = 0, |
||
|
= y(3 / 2) |
(1) |
y'(1/ 2) |
= 0. |
|
Решение.
Произведем замену переменных t=x-1/2, тогда
dy = dy dt = dy d (x − 1/ 2) = dy ,
dx |
dt dx dt |
dx |
dt |
||||
|
d 2 y |
|
= |
d 2 y |
|
|
|
|
dx2 |
dt 2 |
|
|
|||
|
|
|
|
||||
и задачу Штурма-Лиувилля (1) перепишем в виде |
|
||||||
|
y"(t) + λy(t) = 0, |
(2) |
|||||
|
|
|
|
|
|
||
|
y'(0) = y(1) = 0. |
|
|||||
Рассмотрим отдельно случаи, когда параметр l отрицателен, равен нулю или положителен.
1. λ<0.
Пусть l=-m, где m>0. Тогда общее решение уравнения (2) имеет вид
y(t) = C1 exp(
 μt) + C2 exp(-
μt) + C2 exp(-
 μt) .
μt) .
Граничные условия дают:
y'(t) = 
 μ (C1 exp(
μ (C1 exp(
 μt) - C2 exp(-
μt) - C2 exp(-
 μt)),
μt)),
|
y'(0) = C1 - C2 |
= 0 , |
|
|
|
|
|||
|
y(1) = C1 exp( |
|
) + C2 exp(- |
|
) = 0 , |
|
|||
|
μ |
μ |
|||||||
т.е. |
|
C1 (exp( |
|
|
|
|
|
))= 0 . |
|
|
|
|
) + exp(- |
|
|||||
С1=С2 |
и |
μ |
μ |
||||||
Но в рассматриваемом случае m - действительно и положительно, так что
(exp(
 μ ) + exp(-
μ ) + exp(-
 μ ))¹ 0 .
μ ))¹ 0 .
Поэтому
С1=0, С2=0
и, следовательно, y(t)=0, но тривиальные решения нас не интересуют.
2. λ=0.
Общее решение уравнения (2) имеет вид
y(t) = C1t + C2 .
Граничные условия дают:
y'(t) = C1 , y'(0) = C1 = 0 ,
y(1) = C1 ×1+ C2 = 0 ×1+ C2 = C2 = 0 ,
т.е. С1=0, С2=0 и, следовательно,
y(t)=0.
3. λ>0.
Общее решение уравнения может быть записано в виде
43
y(t) = Acos(
 lt) + B sin(
lt) + B sin(
 lt) .
lt) .
Граничные условия дают:
|
|
y'(t) = |
|
|
|
|
(− Asin( |
|
t) + B cos( |
|
|
t)), |
||||||||||
|
l |
l |
l |
|||||||||||||||||||
y'(0) = |
|
(− Asin(0) + B cos(0)) = |
|
|
|
B cos(0) = |
|
|
|
B = 0 B = 0 , |
||||||||||||
l |
l |
l |
||||||||||||||||||||
|
y(1) = Acos( |
|
) + B sin( |
|
|
|
) = Acos( |
|
|
) = 0 . |
||||||||||||
|
l |
|
l |
|
l |
|||||||||||||||||
Если y(t) не равно тождественно нулю, то А¹0, поэтому |
|
|
|
|
||||||||||||||||||
|
|
|
|
) = 0 или |
|
|
|
|
|
|
= p + pn , |
|||||||||||
|
|
cos( |
l |
|
|
|
|
|
l |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
где n=0, 1, 2, … . Следовательно, нетривиальные решения задачи (2) возможны лишь при значениях
|
l = ln |
|
|
p |
|
2 |
|
|
|
|||||
|
= |
+ pn . |
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
Этим собственным значениям соответствуют собственные функции |
|
|||||||||||||
|
yn (t) = An |
|
|
|
|
(2n +1) |
|
|
|
|||||
|
cos |
|
|
|
pt . |
|
||||||||
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Возвращаясь к старой переменной, мы получаем, что только при значениях λ, равных |
|
|||||||||||||
|
l = ln |
|
|
p |
|
2 |
|
|
|
|||||
|
= |
+ pn |
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
существуют нетривиальные решения задачи (1): |
|
|
|
|
||||||||||
|
|
|
(2n + 1) |
|
|
|
|
|||||||
yn |
(x) = An cos |
|
|
|
|
|
|
p (x |
− 1/ 2) . |
|
||||
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
Задача 2. Найти общее решение уравнения, приведя его к каноническому виду. |
|
|||||||||||||
|
49uxx-14uxy+uyy+14ux-2uy=0. |
|
||||||||||||
Краткие теоретические сведения. |
|
|
|
|
|
|
|
|
|
|
|
|||
Общее линейное уравнение с частными производными второго порядка с двумя |
|
|||||||||||||
независимыми переменными имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|||
au xx |
+ 2buxy + cu yy |
+ F (x, y, ux , u y ) = 0 , |
(3) |
|||||||||||
где a, b, c - функции x и y. |
Составим определитель из коэффициентов при старших |
|||||||||||||
производных уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = |
|
a |
|
b |
|
= ac − b2 . |
|
||||||
|
|
|
|
|
||||||||||
|
|
|
b |
|
c |
|
|
|
|
|
|
|
||
Тогда классификация дифференциальных уравнений второго порядка строится в соответствии с классификацией кривых второго порядка:

44
Тип уравнения |
Сигнатура D |
|
|
|
|
|
|
|
|
|
|
|
|
Канонический вид |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривой |
|
|
|
|
второго |
дифференциального |
|||
|
|
порядка |
|
|
|
|
|
уравнения |
|||
Эллиптическое |
D>0 |
|
x |
2 |
|
+ |
|
y |
2 |
= 1 |
uxx+guyy=f |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
уравнение |
|
|
a |
2 |
|
b |
2 |
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Параболическое |
D=0 |
|
|
x = by 2 |
ux+guyy=f |
||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
Гиперболическое |
|
|
x |
2 |
|
− |
y |
2 |
= 1 |
uxx-guyy=f |
|
|
|
|
|
|
|||||||
уравнение |
D<0 |
|
|
|
|
|
|||||
|
a |
2 |
|
|
2 |
|
|||||
|
|
|
|
|
|
|
b |
|
|
|
|
Уравнение |
|
|
|
|
|
|
ady 2 − 2bdydx + cdx2 = 0 |
(4) |
|||||
называется уравнением характеристик для уравнения (3). |
|
|||||
Уравнение (4) эквивалентно двум уравнениям |
|
|||||
ady − (b + |
|
|
|
)dx = 0 |
|
|
b2 |
− ac |
|
||||
|
|
|
|
, |
(5) |
|
ady − (b − |
|
b2 |
− ac |
)dx = 0 |
|
|
Решения уравнений (5) называются характеристиками уравнения (3) которые и определяют замену переменных для приведения уравнения к каноническому виду.
Решение. |
|
|
− 7 |
|
|
|
|
|
Так как D = |
|
49 |
|
= 49 − 7 |
2 |
= 0 , то данное уравнение – параболического типа. |
||
|
|
|||||||
|
− 7 |
1 |
|
|||||
Уравнение характеристик имеет вид |
|
|
(7dy + dx)2 = 0 . |
|||||
49dy 2 |
|
+ 14dydx + dx 2 = 0 |
или |
|||||
Первый интеграл для последнего уравнения есть C=x+7y, поэтому произведем замену
переменных
ξ=x+7y,
η=y.
Тогда получим
ux=uξξx+uηηx= uξ, uxx=(uξ)ξ ξx+(uξ)ηηx= uξξ, uy=uξξy+uηηy=7uξ+ uη,
uyy=(7uξ+ uη)ξξy+(7uξ+ uη)ηηy==49uξξ+7uηξ+7uξη+ uηη=49uξξ+14uηξ+uηη,
uxy=(uξ)ξξy+(uξ)ηηy==7uξξ+uηξ.
Подставляя в исходное дифференциальное уравнение выражения для производных
49uxx-14uxy+uyy+14ux-2uy=0,
49 uξξ-14(7uξξ+uηξ)+49uξξ+14uηξ+uηη+14 uξ-2(7uξ+ uη)=0
получим канонический вид уравнения
uηη+2uη=0

45
с решением
u(h,x)=С1(x)+С2(x)exp(-2h).
Возвращаясь к старым переменным, общее решение исходного уравнения запишем в виде u(x,y)=С1(x+7y)+С2(x+7y)exp(-2y),
где С1(x), С2(x) – произвольные, дважды непрерывно дифференцируемые функции.
Задача 3. Найти общее решение уравнения, приведя его к каноническому виду.
|
|
|
|
|
|
|
|
|
|
2uxx+5uxy-3uyy=0 |
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как |
D = |
|
|
2 |
5 / 2 |
|
= -6 - (5 / 2)2 |
= 49 / 4 < 0 , то |
данное |
уравнение – |
|||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
5 / 2 |
- 3 |
|
|
|
|
|
|
|
|
|
гиперболического типа. |
|
|
|
|
|
|
|
|
|
|
|||||||
Уравнение характеристик имеет вид |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2dy |
2 |
- 5dydx - 3dx |
2 |
= 0 |
|
|
или |
± |
(5 / 2) |
2 |
+ 3 |
|
|||||
|
|
|
|
2dy - 5 / 2 |
|
× 2 dx = 0 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения характеристик мы получили два уравнения
4dy-12dx=0,
4dy+2dx=0
с решениями
С1=12x-4y, C2=2x+4y.
Произведем замену переменных
ξ=12x-4y, η=2x+4y.
Тогда получим ux=uξxx+uηhx= uξ12+uη2,
uxx=(uξ12+uη2)ξ 12+(uξ12+uη2)η2=uξξ122+uηξ24+uξη24+uηη4=122uξξ+48uηξ+4uηη, uy=uξxy+uηhy=-4uξ+4uη, uyy=(-4uξ+4uη)ξxy+(-4uξ+4uη)ηhy=-4(-4uξ+4uη)ξ+4(-4uξ+4uη)η=16uξξ-32uηξ+16uηη, uxy=(uξ12+uη2)ξxy+(uξ12+uη2)ηhy=-4(uξ12+uη2)ξ +4(uξ12+uη2)η=-48 uξξ+40 uηξ+8 uηη.
Подставляя в исходное дифференциальное уравнение выражения для производных
2uxx+5uxy-3uyy=0, 2(122uξξ+48uηξ+4uηη)+5(-48 uξξ+40 uηξ+8 uηη)-3(16uξξ-32uηξ+16uηη)=0
получим канонический вид уравнения
382uηξ=0
с решением
u(h,x)=С1(x)+С2(h).
Возвращаясь к старым переменным, общее решение исходного уравнения запишем в виде u(x,y)=С1(12x-4y)+С2(2x-4y).

46
Задача 4. Решить смешанную задачу.
ut = 9u xx ;
u(x,0) = 31sin(3πx);
u(0, t) = u(1, t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
ut = a 2u xx
имеем
X (x)T '(t) = a 2 X "(x)T (t) .
Здесь a 2 = 9 . После деления на X(x)T(t) получим:
1 T '(t) = X "(x) . |
|
a 2 T (t) |
X (x) |
Это равенство двух отношений, зависящих только от x и только от t, возможно только в случае, если оба отношения равны постоянному числу - l. (l>0):
1 T '(t) = X "(x) = -λ , |
|
a 2 T (t) |
X (x) |
т.е.
X”(x)+ λX(x)=0,
T’(t)+λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями
X”(x)+ λX(x)=0,
X(0)=X(1)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения
X(x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x)
λ x)
сиспользованием краевых условий
X (0) = (A cos(0) + B sin(0)) = A cos(0) = A ×1 = 0 A = 0 ,
X (1) = B sin(1× 
 λ ) = 0 .
λ ) = 0 .
находим собственные значения
λ = λn = (πn)2
и собственные функции
X n (x) = Bn sin(nπx).
47
Второе уравнение системы
T’(t)+λ a 2 T(t)=0
имеет решение
T (t) = C exp(−λa 2t) .
Таким образом, общее решение исходного уравнения принимает вид un (x, t) = X (x)T (t) = Cn exp(−(πna)2 t) sin(πnx) .
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
u(x, t) = ∑Cn exp(−(πna) 2 t) sin(πnx) .
n
Подставляя сюда начальное условие
u(x,0) = ∑Cn sin(πnx) = 31sin(3πx)
n
мы видим, что все константы Cn=0 кроме C3=31. Поэтому окончательный ответ имеет вид
u(x, t) = 31exp(−(3πa) 2 t) sin(3πx) = 31exp(−81π 2t) sin(3πx) .
Задача 5. Решить смешанную задачу.
ut = 2u xx ;
u(x,0) = 31cos(3πx) + cos(4πx);
u x (0, t) = u x (6, t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
|
|
|
u |
t |
= a 2u |
xx |
, |
|
|
|
|
|
|
|
|
|
|
||
имеем |
|
|
|
|
|
|
|||
X (x)T '(t) = a 2 X "(x)T (t) . |
|||||||||
Здесь a 2 = 2 . После деления на X(x)T(t): |
|
|
|
|
|
|
|||
|
1 |
|
T '(t) |
= |
X "(x) |
= −λ |
|||
|
a 2 T (t) |
|
|||||||
|
|
X (x) |
|||||||
получим систему
X”(x)+ λX(x)=0,
T’(t)+λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями:
X”(x)+ λX(x)=0,
X’(0)=X’(6)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения

48
X (x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x) ,
λ x) ,
X'(x) = 
 λ (- Asin(
λ (- Asin(
 λ x) + B cos(
λ x) + B cos(
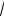 λ x))
λ x))
сиспользованием краевых условий
X '(0) = 
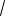 λ (- Asin(0) + B cos(0)) =
λ (- Asin(0) + B cos(0)) = 
 λ B cos(0) = B ×1 = 0 B = 0 ,
λ B cos(0) = B ×1 = 0 B = 0 ,
X '(6) = Asin(6 × 
 λ ) = 0 .
λ ) = 0 .
находим собственные значения
λ = λ = πn 2 n 6
и собственные функции
|
nπ |
|
||
X n (x) = An |
cos |
|
x . |
|
6 |
||||
|
|
|
||
Второе уравнение системы:
T’(t)+l a 2 T(t)=0
имеет решение
T (t) = C exp(-λa 2t) .
Таким образом, общее решение исходного уравнения принимает вид
un (x, t) = X (x)T (t) = Cn |
πn |
|
2 |
πn |
|
exp(- |
6 |
a |
t) cos( |
x) . |
|
|
|
|
|
6 |
|
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
u(x, t) = ∑Cn exp(-(πna / 6) 2 t) cos(πn x) . |
|
n |
6 |
Подставляя сюда начальное условие: |
|
u(x,0) = ∑Cn |
cos(πn x) = 31cos(3πx) + cos(4πx) |
n |
6 |
мы видим, что все константы Cn=0 кроме C18=31 и C24=1. Поэтому окончательный ответ имеет вид
u(x, t) = 31exp(-(3πa)2 t) cos(3πx) + exp(-(4πa)2 t) cos(4πx)
.
u(x, t) = 31exp(-18π 2t) cos(3πx) + exp(-32π 2t) cos(4πx)

49
Задача 6. Решить смешанную задачу.
ut = 7uxx ;
u(x,0) = 3sin(3πx);
u(0,t) = ux (1/ 2,t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
|
|
|
u |
t |
= a 2u |
xx |
, |
|||
|
|
|
|
|
|
|
|
|||
имеем |
|
|
|
|
|
|
|
|||
X (x)T '(t) = a 2 X "(x)T (t) . |
||||||||||
Здесь a 2 = 7 . После деления на X(x)T(t): |
|
|
|
|
|
|
|
|||
|
1 |
|
T '(t) |
= |
X "(x) |
= −λ , |
||||
|
|
|
|
|||||||
|
a 2 T (t) |
|
|
|
X (x) |
|
|
|||
получим систему:
X”(x)+ λX(x)=0,
T’(t)+λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями:
X”(x)+ λX(x)=0,
X(0)=X’(1/2)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения:
X (x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x) ,
λ x) ,
X'(x) = 
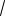 λ (− Asin(
λ (− Asin(
 λ x) + B cos(
λ x) + B cos(
 λ x))
λ x))
сиспользованием краевых условий
X (0) = A cos(0) + B sin(0) = A ×1 = A = 0 ,
X '(1/ 2) = 
 λ (− Asin(
λ (− Asin(
 λ / 2) + B cos(
λ / 2) + B cos(
 λ / 2))=
λ / 2))= 
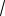 λ B cos(
λ B cos(
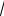 λ / 2) = 0
λ / 2) = 0
находим собственные значения
λ = λn = (π (2n + 1))2
и собственные функции
X n (x) = Bn sin((2n + 1)πx) .
Второе уравнение системы:
T’(t)+λ a 2 T(t)=0
имеет решение
T (t) = C exp(−λa 2t) .
Таким образом, общее решение исходного уравнения принимает вид un (x, t) = X (x)T (t) = Cn exp(−(2n + 1)2 π 2 a 2 t) sin((2n + 1)πx) .
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
u(x, t) = ∑Cn exp(−(2n + 1)2 π 2 a 2t) sin((2n + 1)πx) .
n
Подставляя сюда начальное условие:
50
u(x,0) = ∑Cn sin((2n + 1)πx) = 3sin(3πx)
n
мы видим, что все константы Cn=0 кроме C1=3. Поэтому окончательный ответ имеет вид
u(x, t) = 3exp(−(3πa) 2 t) sin(3πx) . u(x, t) = 3exp(−63πt) sin(3πx)
Задача 7. Решить смешанную задачу.
ut = 5u xx ;
u(x,0) = 7 sin(3πx) − 4 − 5x; u(0, t) = −4;u(1, t) = −9.
Решение.
Введем новую функцию w = w(x, t) , связанную с u(x,t):
u(x, t) = w(x, t) + γ 1 x + γ 2 .
Подберем коэффициенты γ1 и γ2 так, чтобы соответствующее дифференциальное уравнение для w(x, t) = u(x, t) − γ 1 x − γ 2 :
wt = 5wxx |
|
|
имело нулевые граничные условия: |
|
|
w(0, t) = u(0, t) − γ 2 |
= 0 |
|
w(1, t) = u(1, t) − γ 11 − γ |
. |
|
2 = 0 |
||
Подставляя сюда вместо u(0,t) и u(1,t) соответствующие граничные условия получим
систему уравнений для определения γ1 и γ2.
− 4 − γ 2 = 0 . − 9 − γ 11 − γ 2 = 0
Откуда γ2=-4, γ1=-5 и наша новая функция имеет вид w(x, t) = u(x, t) + 5x + 4 . Таким образом, нам необходимо найти решение смешанной задачи для функции w = w(x, t) :
wt = 5wxx
w(x,0) = 7 sin(3πx); w(0, t) = w(1, t) = 0;
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
w(x, t) = X (x)T (t).
Подставляя это выражение в уравнение
|
|
|
w = a 2 w |
xx |
, |
|||
|
|
|
t |
|
|
|
||
имеем |
|
|
|
|
||||
X (x)T '(t) = a 2 X "(x)T (t) . |
||||||||
Здесь a2 = 5 . После деления на X(x)T(t), |
|
|
|
|
||||
|
1 |
|
T '(t) |
= |
X "(x) |
= −λ , |
||
|
|
|
|
|||||
|
a 2 T (t) |
X (x) |
|
|
||||
получим систему
X”(x)+ λX(x)=0,
T’(t)+λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями:
X”(x)+ λX(x)=0,
X(0)=X(1)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения
