
Типовые
.pdf61
с использованием краевых условий получаем собственные значения λ=n и собственные функции
Φ n (ϕ ) = An cos(nϕ ) + Bn sin(nϕ ) .
Решение второго уравнения системы
r2 R”(r) + rR’(r) - λ2R(r)=0
будем искать в виде R(r)=rm, что дает
r2m(m-1)rm-2+rmrm-1- λ2rm=0,
или
rm(m2-λ2)=0
т.е. m=±λ.
Следовательно
R(r) = Cr λ + Dr −λ .
Второе слагаемое необходимо отбросить, поскольку оно дает бесконечность в центре круга: D=0. Таким образом
R(r) = Cr n
и окончательно
un (r,ϕ ) = R(r)Φ(ϕ ) = (An cos(nϕ ) + Bn sin(nϕ ))r n .
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения.
u(r,ϕ ) = ∑(An cos(nϕ ) + Bn sin(nϕ ))r n .
n
Учитывая случай с λ=0 получим
u(r,ϕ ) = A0 + ∑(An cos(nϕ ) + Bn sin(nϕ ))r n .
n=1
Подставляя сюда начальное условие
u(1,ϕ ) = A0 + ∑(An cos(nϕ ) + Bn sin(nϕ ))1n = 31cos(8ϕ ) + 32 sin(9ϕ )
n=1
мы видим, что все константы An=Bn=0 кроме A8=31, B9=32. Поэтому решение исходного уравнения имеет вид
u(r,ϕ ) = 31cos(8ϕ )r 8 + 32 sin(9ϕ )r 9 .

62
Задача 13. Решить смешанную задачу.
utt = 16uxx ;
u(x,0) = 31sin(πx); ut (x,0) = 0;
u(0, t) = u(8, t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
utt = a 2u xx ,
имеем
X (x)T"(t) = a 2 X "(x)T (t) .
Здесь a 2 = 16 . После деления на X(x)T(t) получим
1 T"(t) = X "(x) . |
|
a 2 T (t) |
X (x) |
Это равенство двух отношений, зависящих только от x и только от t, возможно только в случае, если оба отношения равны постоянному числу -l. (l>0):
1 T"(t) = X "(x) = -λ , |
|
a 2 T (t) |
X (x) |
т.е.
X”(x)+ λX(x)=0,
T”(t)+ λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями
X”(x)+ λX(x)=0,
X(0)=X(8)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения
X(x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x)
λ x)
сиспользованием краевых условий
X (0) = A cos(0) + B sin(0) = A cos(0) = A ×1 = 0 A = 0 ,
X (8) = B sin(8 × 
 λ ) = 0 .
λ ) = 0 .
находим собственные значения
λ = λ = πn 2 n 8
и собственные функции
X n (x) = Bn |
πn |
|
|
sin |
8 |
x . |
|
|
|
|
|

63
Второе уравнение системы
T”(t)+ l a 2 T(t)=0
имеет решение
T (t) = C cos(a
 λt) + D sin(a
λt) + D sin(a
 λt) .
λt) .
Таким образом, общее решение исходного уравнения принимает вид
un |
|
cos(a |
πn |
sin(a |
πn |
|
πn |
(x, t) = X (x)T (t) = Cn |
t) + Dn |
8 |
t) sin( |
x) . |
|||
|
|
|
8 |
|
|
8 |
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
|
|
|
πn |
|
πn |
|
|
πn |
|
u(x, t) = ∑ Cn |
cos(a |
t) + Dn sin(a |
t) sin( |
x) . |
|||||
n |
|
|
8 |
|
8 |
|
|
8 |
|
Подставляя сюда начальные условия |
|
|
|
|
|
|
|
||
ut (x, t) = ∑ a |
πn |
|
πn |
|
πn |
|
|
πn |
|
8 |
- Cn sin(a |
t) + Dn cos(a |
t) sin( |
x) , |
|||||
n |
|
|
8 |
|
8 |
|
|
8 |
|
ut (x,0) = ∑ a πn (- Cn × 0 + Dn |
×1)sin(πn x) = 0 Dn |
= 0 , |
|||||||
n |
|
8 |
|
|
8 |
|
|
|
|
u(x,0) = ∑(Cn ×1)sin(πn x) = 31sin(πx) |
|
|
|||||||
|
|
|
n |
|
8 |
|
|
|
|
мы видим, что все константы Cn=0 кроме C8=31. Поэтому окончательный ответ имеет вид
u(x, t) = 31cos(aπt) sin(πx) = 31cos(4πt) sin(πx) .
Задача 14. Решить смешанную задачу.
utt = 16uxx ;
u(x,0) = 31sin(πx); ut (x,0) = 4π sin(πx); u(0, t) = u(8, t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
utt = a 2u xx ,
имеем
X (x)T"(t) = a 2 X "(x)T (t) .
Здесь a 2 = 16 . После деления на X(x)T(t) получим

64
1 T"(t) = X "(x) . |
|
a 2 T (t) |
X (x) |
Это равенство двух отношений, зависящих только от x и только от t, возможно только в случае, если оба отношения равны постоянному числу -l. (l>0):
1 T"(t) = X "(x) = -λ , |
|
a 2 T (t) |
X (x) |
т.е.
X”(x)+ λX(x)=0,
T”(t)+ λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями
X”(x)+ λX(x)=0,
X(0)=X(8)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения
X(x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x)
λ x)
сиспользованием краевых условий
X (0) = (A cos(0) + B sin(0)) = A cos(0) = A ×1 = 0 A = 0 ,
X (8) = B sin(8 × 
 λ ) = 0
λ ) = 0
находим собственные значения
λ = λ = πn 2 n 8
и собственные функции
X n (x) = Bn |
πn |
|
|
sin |
8 |
x . |
|
|
|
|
|
Второе уравнение системы
T”(t)+ l a 2 T(t)=0
имеет решение
T (t) = C cos(a
 λt) + D sin(a
λt) + D sin(a
 λt) .
λt) .
Таким образом, общее решение исходного уравнения принимает вид
un (x, t) = X (x)T (t) = (Cn cos(a
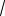 λt) + Dn sin(a
λt) + Dn sin(a
 λt))sin(πn x) . 8
λt))sin(πn x) . 8
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
|
|
πn |
t) + Dn |
πn |
|
πn |
u(x, t) = ∑ Cn |
cos(a |
sin(a |
t) sin( |
x) . |
||
n |
|
8 |
|
8 |
|
8 |
Подставляя сюда начальное условие:

65
u(x,0) = ∑(Cn |
×1)sin(πn x) = 31sin(πx) |
||||
|
n |
|
|
8 |
|
ut (x, t) = ∑ a |
πn |
- Cn |
πn |
cos(a |
|
|
sin(a t) + Dn |
||||
n |
8 |
|
|
8 |
|
C8 = 31 ;
πn |
|
πn |
|
t) sin( |
x) ; |
8 |
|
8 |
ut (x,0) = ∑ a πn (- Cn |
× 0 + Dn |
×1)sin(πn x) = 4π sin(πx) aD8 = 4; D8 = 4 / a = 1 |
|
n |
8 |
|
8 |
мы видим, что все константы Cn=0, Dn=0 кроме C8=31, D8=1. Поэтому окончательный ответ имеет вид
u(x, t) = (31cos(4πt) + sin(4πt))sin(πx) .
Задача 15. Решить смешанную задачу.
utt = 16u xx ;
u(x,0) = 0;
ut (x,0) = 4π cos(πx); u(0, t) = u(7, t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
utt = a 2u xx ,
имеем
X (x)T"(t) = a 2 X "(x)T (t) .
Здесь a 2 = 16 . После деления на X(x)T(t) получим
1 T"(t) = X "(x) . |
|
a 2 T (t) |
X (x) |
Это равенство двух отношений, зависящих только от x и только от t, возможно только в случае, если оба отношения равны постоянному числу -l. (l>0):
1 T"(t) = X "(x) = -λ , |
|
a 2 T (t) |
X (x) |
т.е.
X”(x)+ λX(x)=0,
T”(t)+ λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями
X”(x)+ λX(x)=0,
X(0)=X(7)=0

66
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения
X (x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x) ,
λ x) ,
X'(x) = 
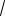 λ (- Asin(
λ (- Asin(
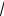 λ x) + B cos(
λ x) + B cos(
 λ x))
λ x))
сиспользованием краевых условий
X '(0) = 
 λ (- A × 0 + B ×1) =
λ (- A × 0 + B ×1) = 
 λ B ×1 = 0 B = 0;
λ B ×1 = 0 B = 0;
X '(7) = 
 λ (- Asin(
λ (- Asin(
 λ 7))= 0
λ 7))= 0 
 λ 7) = πn
λ 7) = πn
находим собственные значения
λ = λ = πn 2 n 7
и собственные функции
X n (x) = An |
πn |
|
|
cos |
7 |
x . |
|
|
|
|
|
Второе уравнение системы
T”(t)+ l a 2 T(t)=0
имеет решение
T (t) = C cos(a
 λt) + D sin(a
λt) + D sin(a
 λt) .
λt) .
Таким образом, общее решение исходного уравнения принимает вид
un (x, t) = X (x)T (t) = (Cn cos(a
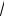 λt) + Dn sin(a
λt) + Dn sin(a
 λt))cos(πn x) . 7
λt))cos(πn x) . 7
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
|
|
|
πn |
|
πn |
|
πn |
x) . |
|
u(x, t) = ∑ Cn |
cos(a |
t) + Dn sin(a |
t) cos( |
|
|||||
|
n |
|
7 |
|
7 |
|
7 |
|
|
Подставляя сюда начальное условие: |
|
|
|
|
|
|
|||
u(x,0) = ∑(Cn cos(0) + Dn |
sin(0))cos(πn x) = |
∑Cn cos(πn x) =0 Cn = 0; |
|||||||
n |
|
|
|
7 |
n |
|
7 |
|
|
ut (x, t) = ∑a |
πn |
|
πn |
|
πn |
|
πn |
x) ; |
|
- Cn sin(a |
t) + Dn |
cos(a |
t) cos( |
||||||
|
n |
7 |
|
7 |
|
7 |
|
7 |
|
ut (x,0) = ∑ a πn Dn cos(πn x) = 4π cos(πx) aD7 |
= 4; D7 |
= 4 / a = 1 |
|||||||
n |
7 |
|
7 |
|
|
|
|
|
|
мы видим, что все константы Cn=0, Dn=0 кроме D7=1. Поэтому окончательный ответ имеет вид
u(x, t) = sin(4πt) cos(πx) .

67
Задача 16. Решить смешанную задачу.
utt = 81u xx ;
u(x,0) = 0;
ut (x,0) = 9π sin(πx);
u(0, t) = u x (5 / 2, t) = 0.
Решение.
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
u(x,t) = X (x)T (t).
Подставляя это выражение в уравнение
utt = a 2u xx ,
имеем
X (x)T"(t) = a 2 X "(x)T (t) .
Здесь a 2 = 81. После деления на X(x)T(t) получим
1 T"(t) = X "(x) . |
|
a 2 T (t) |
X (x) |
Это равенство двух отношений, зависящих только от x и только от t, возможно только в случае, если оба отношения равны постоянному числу -l. (l>0):
1 T"(t) = X "(x) = -λ , |
|
a 2 T (t) |
X (x) |
т.е.
X”(x)+ λX(x)=0,
T”(t)+ λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями
X”(x)+ λX(x)=0,
X(0)=X’(5/2)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения
X (x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x) ,
λ x) ,
X'(x) = 
 λ (- Asin(
λ (- Asin(
 λ x) + B cos(
λ x) + B cos(
 λ x))
λ x))
сиспользованием краевых условий
X (0) = (A ×1 + B × 0) = A ×1 = 0 A = 0;
X '(5 / 2) = 
 λ (- B cos(
λ (- B cos(
 λ 5 / 2))= 0
λ 5 / 2))= 0 
 λ 5 / 2) = 2n + 1π 2
λ 5 / 2) = 2n + 1π 2
находим собственные значения

|
|
|
68 |
|
|
|
|
λ = λn |
|
π (2n + 1) 2 |
|
||
|
= |
5 |
|
|
||
|
|
|
|
|
|
|
и собственные функции |
|
|
|
π (2n + 1) |
|
|
X n |
(x) = An |
|
|
|||
sin |
|
5 |
x . |
|||
|
|
|
|
|
|
|
Второе уравнение системы
T”(t)+ λ a 2 T(t)=0
имеет решение
T (t) = C cos(a
 λt) + D sin(a
λt) + D sin(a
 λt) .
λt) .
Таким образом, общее решение исходного уравнения принимает вид
un (x, t) = X (x)T (t) = (Cn cos(a
 λt) + Dn sin(a
λt) + Dn sin(a
 λt))sin(π (2n + 1) x) . 5
λt))sin(π (2n + 1) x) . 5
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
|
|
π (2n + 1) |
π (2n + 1) |
|
π (2n + 1) |
||||
u(x, t) = ∑ Cn |
cos(a |
5 |
t) + Dn sin(a |
5 |
|
t) sin( |
5 |
x) . |
|
n |
|
|
|
|
|
|
|||
Подставляя сюда начальное условие: |
|
|
|
|
|
|
|||
u(x,0) = ∑(Cn cos(0) + Dn sin(0))sin(π (2n + 1) x) = |
∑Cn |
sin(π (2n + 1) x) =0 Cn = 0; |
|||||||
n |
|
|
|
5 |
n |
|
5 |
|
|
π (2n + 1) |
π (2n + 1) |
cos(a |
π (2n + 1) |
|
π (2n + 1) |
||||
ut (x, t) = ∑a |
5 |
− Cn |
sin(a |
t) + Dn |
|
5 |
t) sin( |
x) ; |
|
n |
|
|
5 |
|
|
|
5 |
||
ut (x,0) = ∑ a π (2n + 1) Dn |
sin(π (2n + 1) x) = 9π sin(πx) aD2 = 9; D2 |
= 9 / a = 1 |
|||||||
n |
5 |
|
|
5 |
|
|
|
|
|
мы видим, что все константы Cn=0, Dn=0 кроме D2=1. Поэтому окончательный ответ имеет вид
u(x, t) = sin(9πt) sin(πx) .
Задача 17. Решить смешанную задачу.
utt = 4uxx ;
u(x,0) = 31sin(2πx) − 1 + 3x;
ut (x,0) = 0;
u(0, t) = −1;u(2, t) = 5.
Решение.
Введем новую функцию w = w(x, t) , связанную с u(x,t):
w(x, t) = u(x, t) + γ 1 x + γ 2 .
Подберем коэффициенты γ1 и γ2 так, чтобы соответствующее дифференциальное уравнение для w = w(x, t) :

69
wtt = 4wxx ,
имело нулевые граничные условия:
w(0, t) = u(0, t) + γ 2 = 0 , w(2, t) = u(2, t) + γ 1 2 + γ 2 = 0 .
Подставляя сюда вместо u(0,t) и u(2,t) соответствующие граничные условия получим систему уравнений для определения γ1 и γ2:
− 1 + γ 2 = 0 5 + 2γ 1 + γ 2 = 0
.
Откуда γ2=1, γ1=-3 и наша новая функция имеет вид w(x, t) = u(x, t) − 3x + 1. Таким образом, нам необходимо найти решение смешанной задачи для функции w = w(x, t) :
wtt = 4wxx ,
w(x,0) = 31sin(2πx) , w(0, t) = w(2, t) = 0 .
Будем искать (не равное нулю) решение уравнения в виде произведения двух функций, одна из которых зависит только от x, а другая – только от t, т.е.
w(x, t) = X (x)T (t).
Подставляя это выражение в уравнение
|
|
|
w |
= a 2 w |
xx |
, |
||
|
|
|
tt |
|
|
|
|
|
имеем |
|
|
|
|
|
|||
X (x)T '(t) = a 2 X "(x)T (t) . |
||||||||
Здесь a 2 = 4 . После деления на X(x)T(t): |
|
|
|
|
|
|||
|
1 |
|
T '(t) |
= |
X "(x) |
= −λ |
||
|
a 2 T (t) |
|
||||||
|
|
X (x) |
|
|
||||
получим систему
X”(x)+ λX(x)=0,
T”(t)+ λ a 2 T(t)=0.
Первое уравнение системы с граничными условиями
X”(x)+ λX(x)=0,
X(0)=X(2)=0
представляет собой задачу Штурма-Лиувилля на отыскание собственных функций и собственных значений дифференциального оператора (см. задачу 1). Из общего решения уравнения
X (x) = A cos(
 λ x) + B sin(
λ x) + B sin(
 λ x)
λ x)

70
с использованием краевых условий
X (0) = A cos(0) + B sin(0) = A ×1 = A = 0 ,
X (2) = B sin(2
 λ ) = 0
λ ) = 0
находим собственные значения
λ = λ = πn 2 n 2
и собственные функции
X n (x) = Bn sin(πn x) . 2
Второе уравнение системы
T”(t)+ λ a 2 T(t)=0
имеет решение
T (t) = C cos(a
 λt) + D sin(a
λt) + D sin(a
 λt) .
λt) .
Таким образом, общее решение исходного уравнения принимает вид
wn (x, t) = X (x)T (t) = (Cn cos(a
 λt) + Dn sin(a
λt) + Dn sin(a
 λt))sin(πn x) . 2
λt))sin(πn x) . 2
Поскольку при любых n полученная функция является решением нашего дифференциального уравнения, то и сумма этих решений так же будет являться решением исходного дифференциального уравнения:
|
|
|
πn |
|
πn |
|
πn |
x) . |
w(x, t) = ∑ Cn cos(a |
t) + Dn sin(a |
t) sin( |
||||||
n |
|
|
2 |
|
2 |
|
2 |
|
Подставляя сюда начальное условие: |
|
|
|
|
|
|
|
|
wt (x, t) = ∑ a |
πn |
− Cn |
sin(a |
πn |
|
πn |
|
πn |
|
t) + Dn cos(a |
t) sin( x) ; |
||||||
n |
2 |
|
|
2 |
|
2 |
|
2 |
wt (x,0) = ∑a πn Dn |
sin(πn x) = 0 Dn |
= 0; |
|
|||||
|
|
n |
2 |
2 |
|
|
|
|
w(x,0) = ∑(Cn cos(0) + Dn sin(0))sin(πn ) = ∑Cn |
sin(πn x) =31sin(2πx) C4 = 31; |
|||||||
n |
|
|
2 |
n |
2 |
|
|
|
мы видим, что все константы Cn=0, Dn=0 кроме C4=31. Поэтому ответ имеет вид
w(x, t) = 31cos(4πt) sin(2πx) .
Переходя к старой функции u(x, t) = w(x, t) + 3x − 1 получим окончательный ответ
u(x, t) = 31cos(4πt) sin(2πx) + 3x − 1 .
