2. Сети Петри с переходами «исключающее или».

Наряду с обычными переходами, готовность к срабатываниям для которых по отношению к входным дугам реализует дисциплину «и», в сети могут использоваться переходы, реализующие дисциплину «исключающее или »: переход может сработать, если только в одной из входных позиций есть фишки, а в остальных – фишек нет. Если для некоторой позиции , то переход может сработать при некоторой маркировке , если , а если , то – только если . Если , то как и для обычных переходов значение не влияет на возможность срабатывания перехода . Графическое изображение таких переходов должно каким-то образом отличаться от графического изображения обычных переходов (например, оно может быть таким, как изображено на рис. 19).

2. Другой вариант сетей с раскрашенными фишками.

Известны и другие варианты определния сетей Петри с раскрашенными фишками, для которых требование конечности множества красок не обязательно. Одно из них формулируется так. В определении сети по иному определяются компоненты, определяющие связи между позициями и переходами: , т.е. для всех переходов задаются кортежи входных и выходных позиций. Маркировки с цветными фишками определяются так же, как и ранее, т.е. маркировка. В условии срабатывания и в функции изменения маркировкипри срабатывании переходакортежи входных и выходных позиций рассматриваются как комплекты, т.е. неупорядоченные наборы из тех элементов. Дополнительно задается функция, такая, что для всехи если-й компонент кортежаимеет числовое значение, то оно лежит в диапазоне. Если-й компонент кортежапредставлен цветом из, то при любом срабатывании перехода по-му выходу выдается фишка указанного цвета, а если-й компонент кортежаимеет числовое значение, то по-му выходу выдается фишка того же цвета, какого была фишка, удаленная из-ой входной позиции перехода.

2. Равносильность и универсальность расширений.

Все варианты расширений понятия сети Петри, в которых условие срабатывания переходов связано с отсутствием фишек в некоторых позициях, оказываются равносильными и настолько расширяющими возможности формализма сетей Петри, что с использованием любого из этих вариантов расширения, с одной стороны, можно моделировать любые универсальные уточнения понятия алгоритма и вычислимой функции (машины Тьюринга, вычисления на абаке, алгорифмы Маркова и т.д.). С другой стороны, это приводит и к неразрешимости большинства из теоретических проблем для расширенных систем, которые являются полуразрешимыми и даже разрешимыми для более слабых систем.

Для примера покажем, как сети Петри с ингибиторными дугами могут моделировать произвольные вычисления на абаке.

Напомним, что алгоритм вычислений на абаке задается с помощью управляющего графа со специальной терминальной вершиной и двумя видами вершин из конечных не пересекающихся подмножестви(). Множество всех вершин управляющего графа обозначим(). Все вершины изипомечены элементами конечного множествапеременных с помощью функции . Функции,определяют исходящие из вершин дуги (из терминальной вершины дуги не исходят). Любоесостояние абака задается как комплект переменных, т.е..Начальное состояние абака обозначим . Результат вычислений для начального состояния абакаопределяется как значениефункции, в общем случае частичной:

Таким образом, всякий абак задается как пара , где– управляющий граф, а– начальное состояние абака.

Известно, что на абаке вычислима любая унарная частично-рекурсивная функция, т.е., согласно тезису А. Черча, любая рекурсивная (интуитивно-вычислимая) функция . Т.е. для любой заданной УЧРФможно построить управляющий граф вычислений на абаке, выделить произвольную переменнуюи задать начальное состояние, такое, чтопредставляет значение аргументаэтой функции, то если значениеопределено, то существует заключительное состояние, такое, что а– значение. Не ограничивая общности положим, чтодля всех других переменных, отличных от().

Пусть задан конкретный абак . Построим сеть Петри,с ингибиторными дугами по следующим правилам:

• множество позиций 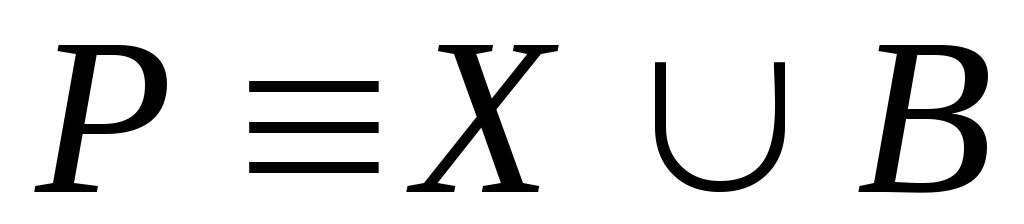, где– подмножество позиций, взаимно однозначно сопоставленных переменным абака,– подмножество позиций, взаимно однозначно сопоставленных вершинам управляющего графа (первого вида – с одной исходящей дугой, второго вида – с двумя исходящими дугами и заключительной вершине – без исходящих дуг);

• множество переходов , где– подмножество переходов, взаимно однозначно сопоставленных вершинам управляющего графа первого вида,и– два подмножества переходов, взаимно однозначно сопоставленных вершинам управляющего графа второго вида,

• начальная маркировка определяется так: если, то, иначеи;.

• компоненты иллюстрирует рис. 20.

• заключительное состояние абака (если оно существует) представлено подмаркировкой на подмножестве позицийединственно возможно достижимой тупиковой маркировкой, такой, чтои.