Методички / Markov

Алгорифмы Маркова.

П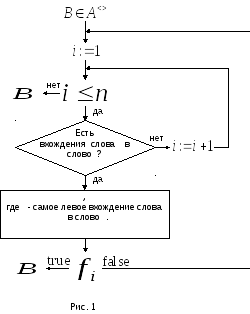 усть - алфавит, - исходное данное (произвольное слово в алфавите ). Запись нормального алгорифма над есть кортеж из произвольного конечного числа подстановок. Далее обозначает количество подстановок в алгорифме. Каждая -я подстановка, , задается тройкой , где (левая часть подстановки) и (правая часть подстановки) - произвольные слова в алфавите (), а определяет вид подстановки: для заключительной подстановки и для обычной подстановки. В литературе принято представление записи нормального алгорифма, в котором подстановки изображаются в порядке перечисления на отдельных строках в следующем виде: для обычных подстановок и для заключительных подстановок, .

Алгоритм применения алгорифма к исходному данному определен блок-схемой, показанной на рис. 1.

График функции , вычислимой нормальным алгорифмом (вычислимой по Маркову), есть множество пар слов начальных и заключительных значений переменной . В общем случае функция является частичной, так как процесс применения алгоритма выполнения может продолжаться неограниченно долго.

Тезис Маркова. Любая интуитивно вычислимая функция из в вычислима некоторым нормальным алгорифмом.

Нетрудно видеть, что с точностью до кодирования любая вычислимая по Маркову функция над произвольным алфавитом может быть вычислена нормальным алгорифмом над двухбуквенным алфавитом . Действительно, определим коды букв алфавита и слов из следующим образом. Если - произвольным образом упорядоченное множество букв алфавита , то коды букв и слов определим так:

,

.

Пусть - самое левое вхождение слова в слово . Очевидно, что при описанном кодировании код результата замены в этого вхождения на слово может быть получен как результат замены в коде слова самого левого вхождения кода слова на код слова . Отсюда следует, что если во всех подстановках исходного алгорифма заменить левые и правые части на их коды, то в результате применения полученного таким образом алгорифма к коду любого слова будет получен код слова-результата применения исходного алгорифма к слову .

Челночные алгорифмы

Пусть - алфавит нормального алгорифма и ( - свободное объединение), где

• - основной алфавит,

• - дополнительный алфавит,

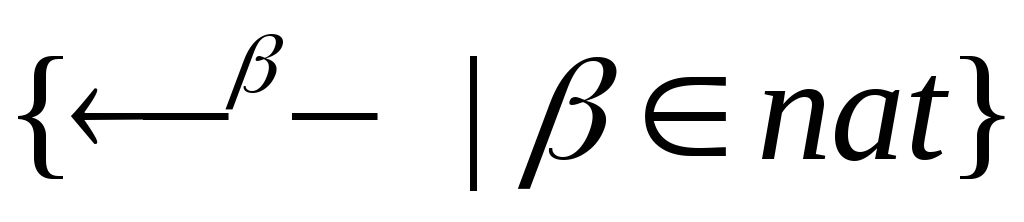• - множество «правосторонних челноков»,

• - множество «левосторонних челноков».

«Челночным» называется алгорифм вида

…

, где

…

Пусть задан нормальный алгорифм

Эквивалентный челночный алгоритм может быть определен так, как показано на рис. 1 (здесь ).

Рассмотрим вопрос трансляции машин Тьюринга в подкласс челночных алгоритмов. Напомним, что машина Тьюринга есть автомат, состоящий из разделенной на клетки бесконечной в обе стороны ленты с одной выделенной «активной» клеткой и управляющего блока. В клетках записаны символы из множества , называемого внешним алфавитом машины, где - символ «пустой» клетки, причем только в конечном числе клеток могут быть записаны символы, отличные от . В любой момент времени управляющий блок может находиться в одном из конечного множества состояний, где - состояние «останова». Множество называют также внутренним алфавитом машины, а состояние м ашины, включающее состояние ленты с выделенной клеткой и состояние управляющего блока, - конфигурацией.

Одной из форм задания поведения машины (изменений конфигураций) является табличная форма, в которой строки соответствуют состояниям управляющего блока (кроме состояния ), а столбцы – символам внешнего алфавита. Элементы таблицы описывают изменение конфигурации, в которой - состояние управляющего блока, а - символ в выделенной клетке на ленте: определяет новое состояние управляющего блока, - символ, на который замещается символ в выделенной клетке ленты, а - изменение положения выделенной клетки на ленте. Символ означает продвижение влево по ленте, - продвижение вправо, а - без изменения положения выделенной клетки на ленте.

Не ограничивая общности, будем считать, что начальное состояние управляющего блока есть , а выделенной клеткой на ленте является самая левая клетка, в которой записан символ, отличный от (если лента «пуста», то выделенной можно считать любую клетку). Потребуем также, чтобы этому требованию удовлетворяли все конфигурации останова (при состоянии управляющего блока).

Сопоставим каждому состоянию машины Тьюринга два челнока: и . Введем для этих челноков подстановки:

Если для случая при переборе состояний управляющего блока мы «зациклимся», то выберем в качестве правой части соответствующей подстановки, что приведет и к зацикливанию процесса применения определяемого челночного алгоритма.

7