
В.Н. Фальк
Формальные языки.
Класс регулярных языков
Учебное пособие
Учебное пособие предназначено для аудиторной и самостоятельной работы студентов всех специальностей дневного и заочного отделений Института информационных технологий РГСУ при изучении дисциплин «Математическая логика и теория алгоритмов» и «Дискретная математика». Электронная версия пособия размещена в интернете:
(http://falkvn.narod.ru/dlya_studentov/RegularFormalLanguages.rar).
По материалу пособия предусмотрено выполнение индивидуального контрольного задания, генератор которого также размещен в интернете
(http://falkvn.narod.ru/dlya_studentov/ZadanieRFL.rar)
Формальные языки класс регулярных языков
Основные определения.
Алфавит – конечное множество, элементы которого называют символами или буквами.
![]() – количество букв
в алфавите
– количество букв
в алфавите
![]() .
.
![]() – равно по
определению.
– равно по
определению.
![]() – множество
натуральных чисел.
– множество
натуральных чисел.
![]() – интервал
(подмножество следующих друг за другом
натуральных чисел).
– интервал
(подмножество следующих друг за другом
натуральных чисел).
![]() – слово в
алфавите
– слово в
алфавите
![]() ,
,
![]() – длина
слова
– длина
слова
![]() ,
,
![]() –
–
![]() -я
буква слова
-я
буква слова
![]() .
.
Формальный язык
в алфавите
![]() – множество слов в алфавите
– множество слов в алфавите
![]() .
.
![]() – пустое слово,
– пустое слово,
![]() .
.
![]() – слово –
конкатенация
слов
– слово –
конкатенация
слов
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
![]() – класс конечных
формальных языков.
– класс конечных
формальных языков.
Операции на
множестве формальных языков: объединение
(![]() ),
конкатенация (
),
конкатенация (![]() ),
итерация (*):
),
итерация (*):
![]() ,
,
![]() ,
,
![]() .
.
![]() – класс регулярных
формальных языков, замыкание класса
конечных языков относительно операций
объединения, конкатенации и итерации.
– класс регулярных
формальных языков, замыкание класса
конечных языков относительно операций
объединения, конкатенации и итерации.
Замыкание
множества
(класса)
![]() относительно множества операций
относительно множества операций
![]() – наименьшее множество (класс), включающий
– наименьшее множество (класс), включающий
![]() и замкнутый относительно операций из
и замкнутый относительно операций из
![]() .
.
Множество
![]() (класс) замкнуто
относительно
(класс) замкнуто
относительно
![]() -арной
операции
-арной
операции
![]() ,
если
,
если
![]() .
.
Графом называется
пара
![]() ,
где
,
где
![]() – конечное множество вершин графа, а
– конечное множество вершин графа, а
![]() – компонент, определяющий связи между
вершинами графа. Различные виды
графов задаются возможными комбинациями
значений трех классифицирующих признаков
– компонент, определяющий связи между
вершинами графа. Различные виды
графов задаются возможными комбинациями
значений трех классифицирующих признаков
![]() .
.
![]() означает, что граф – обыкновенный
(
означает, что граф – обыкновенный
(![]() – подмножество
возможных связей между вершинами),
– подмножество
возможных связей между вершинами),
![]() соответствует понятию мультиграфа
(
соответствует понятию мультиграфа
(![]() – комплект
возможных связей между вершинами).
– комплект
возможных связей между вершинами).
![]() означает, что связи между вершинами не
ориентированы
(симметричны). Такие связи называются
ребрами
графа и при графическом представлении
графов изображаются линиями, связывающими
представляющие вершины графа пары точек
означает, что связи между вершинами не
ориентированы
(симметричны). Такие связи называются
ребрами
графа и при графическом представлении
графов изображаются линиями, связывающими
представляющие вершины графа пары точек
![]() .
.
![]() означает, что связи рассматриваются
как ориентированные.
Такие связи называются дугами
графа и при графическом представлении
графов изображаются линиями с указанием
направления связи.
означает, что связи рассматриваются
как ориентированные.
Такие связи называются дугами
графа и при графическом представлении
графов изображаются линиями с указанием
направления связи.
![]() означает отсутствие петель
(связь возможна только между различными
вершинами графа, для обыкновенных графов
это означает, что
означает отсутствие петель
(связь возможна только между различными
вершинами графа, для обыкновенных графов
это означает, что
![]() как бинарное отношение на
как бинарное отношение на
![]() является антирефлексивным), а
является антирефлексивным), а
![]() предполагает возможность петель в
графе. Комбинации значений признаков
предполагает возможность петель в
графе. Комбинации значений признаков
![]() и
и
![]() позволяют уточнить понятие связи между
вершинами следующим образом:
позволяют уточнить понятие связи между
вершинами следующим образом:
|
|
|
Связь
между вершинами
|
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
|
Взвешенным (нагруженным) графом называется граф с дополнительно заданным отображением его вершин или связей в некоторое множество, называемое множеством весов.
Известны три основных способа задания регулярных языков:
-
с помощью языка регулярных выражений,
-
путем задания конечного автомата,
-
путем задания графа переходов.
Язык регулярных выражений.
Определим язык
регулярных выражений, интерпретированных
как множества слов в некотором алфавите
![]() .
Интерпретацию выражения
.
Интерпретацию выражения
![]() будем обозначать как
будем обозначать как
![]()
![]() .
.
Синтаксис:
-
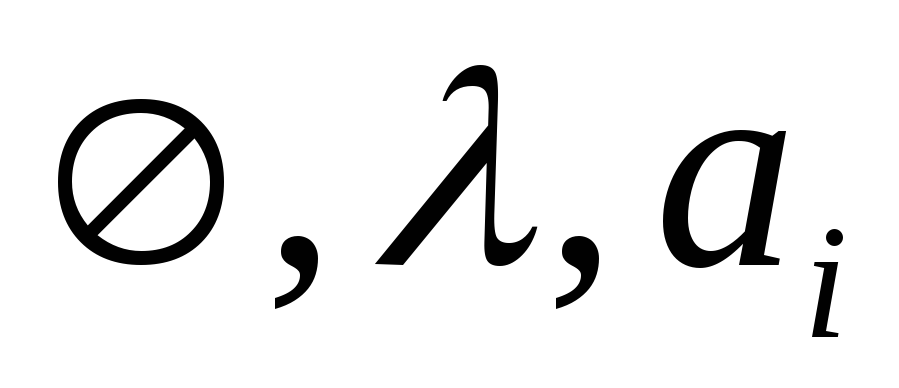 (для всех
(для всех
 )
суть регулярные выражения.
)
суть регулярные выражения.
-
Если
 ,
,
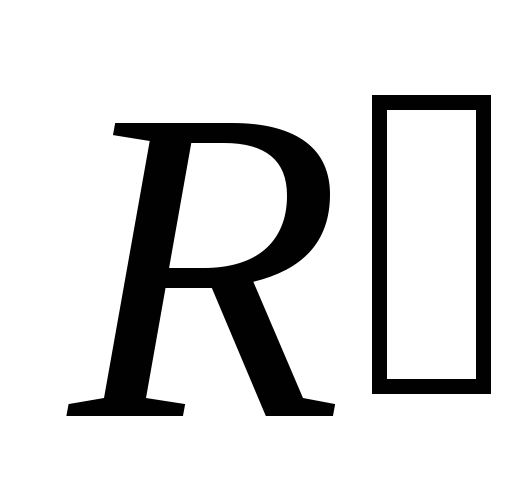 и
и
 – регулярные выражения, то
– регулярные выражения, то
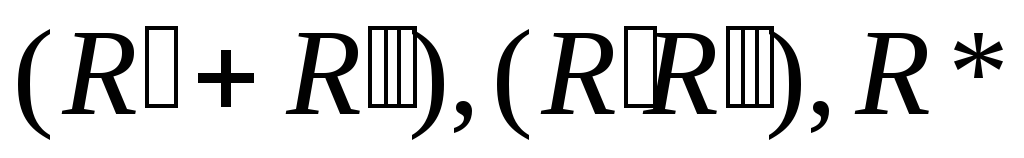 – регулярные выражения.
– регулярные выражения. -
Других регулярных выражений, кроме полученных согласно п.п. 1,2, нет.
Внешние и часть внутренних скобок может быть опущена согласно принятому приоритету операций: итерация, конкатенация, объединение (в порядке уменьшения приоритета), а также с учетом ассоциативности операций объединения и конкатенации (см. ниже).
Интерпретация:
![]()
![]()
![]() – пустое множество
слов,
– пустое множество
слов,
![]()
![]()
![]() – множество,
содержащее единственное пустое слово,
– множество,
содержащее единственное пустое слово,
![]()
![]()
![]() – множество,
содержащее единственное однобуквенное
слово
– множество,
содержащее единственное однобуквенное
слово
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
– объединение
множеств
– объединение
множеств
![]()
![]()
и
и
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
– конкатенация
множеств
– конкатенация
множеств
![]()
![]()
и
и
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() – итерация множества
– итерация множества
![]()
![]() .
.
Очевидно, что язык
регулярных выражений в интерпретации
представляет в точности класс регулярных
множеств. Действительно, согласно
определению класса регулярных языков,
любое регулярное множество слов может
быть получено применением операций
объединения, конкатенации и итерации
к конечным множествам слов. Так как
используемые при построении регулярных
выражений связки
![]() ,
,
![]() и * интерпретируются как указанные
выше операции, то достаточно показать,
что любое конечное множество слов
является интерпретацией некоторого
регулярного выражения. Если это множество
пусто, то достаточно выбрать константу
и * интерпретируются как указанные
выше операции, то достаточно показать,
что любое конечное множество слов
является интерпретацией некоторого
регулярного выражения. Если это множество
пусто, то достаточно выбрать константу
![]() ,
в противном случае любое конечное
множество можно получить операцией
объединения множеств, каждое из которых
содержит единственное слово. Если это
пустое слово, то это множество является
интерпретацией константы
,
в противном случае любое конечное
множество можно получить операцией
объединения множеств, каждое из которых
содержит единственное слово. Если это
пустое слово, то это множество является
интерпретацией константы
![]() ,
в противном случае множество с единственным
словом
,
в противном случае множество с единственным
словом
![]() ,
,
![]() ,
может быть получено конкатенацией
множеств с единственными однобуквенными
словами
,
может быть получено конкатенацией
множеств с единственными однобуквенными
словами
![]() ,
,
![]() ,
… ,
,
… ,
![]() ,
соответственно, представленных в
интерпретации соответствующими
константами из числа
,
соответственно, представленных в
интерпретации соответствующими
константами из числа
![]() ,
… ,
,
… ,
![]() .
С другой стороны, константы языка
регулярных выражений интерпретируются
только как конечные множества слов,
следовательно, в силу замкнутости класса
регулярных множеств слов, все регулярные
выражения интерпретируются как регулярные
множества.
.
С другой стороны, константы языка
регулярных выражений интерпретируются
только как конечные множества слов,
следовательно, в силу замкнутости класса
регулярных множеств слов, все регулярные
выражения интерпретируются как регулярные
множества.
Для языка регулярных
схем
(в язык регулярных выражений добавлено
счетное множество
![]() переменных,
областью значений которых являются
произвольные множества слов в
рассматриваемом алфавите) можно построить
исчисление
эквивалентностей,
обладающее свойствами непротиворечивости
и полноты.
В качестве переменных будем использовать
символы
переменных,
областью значений которых являются
произвольные множества слов в
рассматриваемом алфавите) можно построить
исчисление
эквивалентностей,
обладающее свойствами непротиворечивости
и полноты.
В качестве переменных будем использовать
символы
![]() ,
возможно, с индексами и штрихами. Всякая
интерпретация схем задается интерпретацией
,
возможно, с индексами и штрихами. Всякая
интерпретация схем задается интерпретацией
![]() переменных. Интерпретацию схемы
переменных. Интерпретацию схемы
![]() ,
индуцированную интерпретацией
,
индуцированную интерпретацией
![]() переменных, будем обозначать
переменных, будем обозначать
![]()
![]() .
По определению,
.
По определению,
![]()
![]()
![]()
![]() .
Очевидно, что интерпретация конкретной
схемы вполне определяется интерпретацией
только входящих в эту схему переменных.
Система аксиом
исчисления отражает свойства операций
объединения, конкатенации и итерации,
их связь с константами и некоторые
взаимосвязи указанных операций. Ниже
приведен один из возможных вариантов
системы и правил
вывода
исчисления эквивалентности регулярных
схем. Формулы этого исчисления имеют
вид
.
Очевидно, что интерпретация конкретной
схемы вполне определяется интерпретацией
только входящих в эту схему переменных.
Система аксиом
исчисления отражает свойства операций
объединения, конкатенации и итерации,
их связь с константами и некоторые
взаимосвязи указанных операций. Ниже
приведен один из возможных вариантов
системы и правил
вывода
исчисления эквивалентности регулярных
схем. Формулы этого исчисления имеют
вид
![]() ,
где
,
где
![]() и
и
![]() – регулярные схемы. Непротиворечивость
исчисления означает, что для всякой
выводимой в исчислении формулы
– регулярные схемы. Непротиворечивость
исчисления означает, что для всякой
выводимой в исчислении формулы
![]() справедливо утверждение
справедливо утверждение
![]()
![]() =
=![]()
![]()
![]() ,
а полнота предполагает, что из истинности
утверждения
,
а полнота предполагает, что из истинности
утверждения
![]()
![]() =
=![]()
![]()
![]() следует, что формула
следует, что формула
![]() выводима в этом исчислении.
выводима в этом исчислении.
Аксиомы:
![]() (рефлексивность
объединения),
(рефлексивность
объединения),
![]() (коммутативность
объединения),
(коммутативность
объединения),
![]() (ассоциативность
объединения),
(ассоциативность
объединения),
![]() (аддитивный ноль
для объединения),
(аддитивный ноль
для объединения),
![]() (ассоциативность
конкатенации),
(ассоциативность
конкатенации),
![]() (мультипликативная
единица для конкатенации),
(мультипликативная
единица для конкатенации),
![]() (мультипликативный
ноль для конкатенации),
(мультипликативный
ноль для конкатенации),
![]() (идемпотентность
итерации),
(идемпотентность
итерации),
![]() ,
,
![]() (итерация как
минимальное решение уравнения
(итерация как
минимальное решение уравнения
![]() или
или
![]() ),
),
![]() ,
,
![]() (дистрибутивность
конкатенации относительно объединения),
(дистрибутивность
конкатенации относительно объединения),
![]() ,
,
![]() .
.
Правила вывода:
P1:
![]() ;
;
P2:
![]() ;
;
P3:
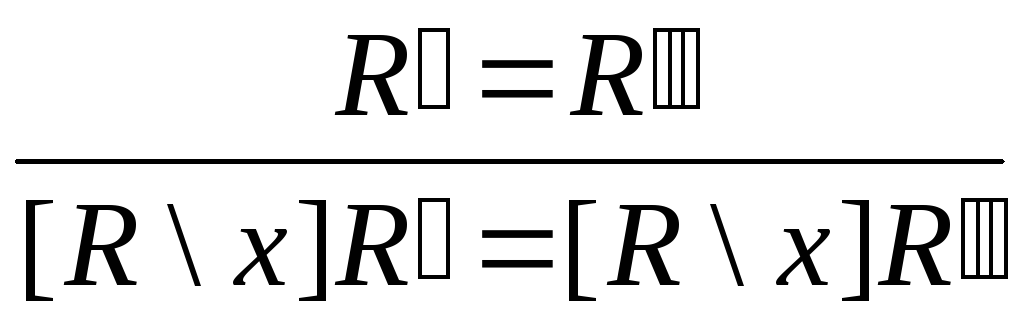 (
(![]() означает результат подстановки схемы
означает результат подстановки схемы
![]() в схему
в схему
![]() вместо всех вхождений в нее переменной
вместо всех вхождений в нее переменной
![]() );
);
P4.1:
![]() ;
P4.2:
;
P4.2:
![]() ;
P4.3:
;
P4.3:![]() ;
;
P4.4:
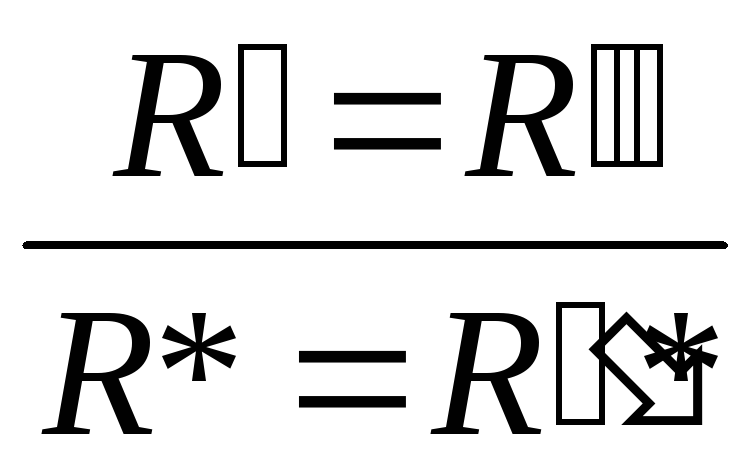 ;
;
P5:
![]() ,
где
,
где
![]()
![]()
![]() и в случае, когда
и в случае, когда
![]() не содержит переменных может быть
вычислено согласно следующим правилам
вычисления:
не содержит переменных может быть
вычислено согласно следующим правилам
вычисления:
![]()
Конечные автоматы.
Второй способ
задания регулярных языков базируется
на понятии конечного
автомата.
Пусть задан алфавит
![]() .
Конечным автоматом над этим алфавитом
называется специального вида взвешенный
ориентированный мультиграф с множеством
вершин
.
Конечным автоматом над этим алфавитом
называется специального вида взвешенный
ориентированный мультиграф с множеством
вершин
![]() ,
называемых состояниями
автомата, возможно, с петлями, в котором
выделена одна начальная вершина
,
называемых состояниями
автомата, возможно, с петлями, в котором
выделена одна начальная вершина
![]() (начальное
состояние
автомата) и произвольное подмножество
вершин
(начальное
состояние
автомата) и произвольное подмножество
вершин
![]() – заключительных
состояний
автомата. Специальным требованиями
является наличие у каждой вершины в
точности
– заключительных
состояний
автомата. Специальным требованиями
является наличие у каждой вершины в
точности
![]() исходящих дуг, весами которых являются
различные буквы алфавита
исходящих дуг, весами которых являются
различные буквы алфавита
![]() .
Формальным языком
.
Формальным языком
![]()
![]()
(множество слов в алфавите
(множество слов в алфавите
![]() ),
представленным
конечным автоматом
),
представленным
конечным автоматом
![]() ,
назовем множество слов-весов всевозможных
путей в графе автомата, ведущих из
начального состояния автомата в любое
из заключительных состояний. Напомним,
что путем
в графе из одной его вершины в другую
называется последовательность дуг
(если эта последовательность пустая,
то начальная вершина пути одновременно
является и концевой вершиной), такая,
что первая дуга исходит из начальной
вершины пути, а любая из остальных – из
вершины, в которую заходит предшествующая
дуга, причем последняя дуга пути заходит
в его концевую вершину. Весом
пути назовем
слово-конкатенацию весов отдельных
дуг, образующих этот путь. Заметим, что
язык, представленный конечным автоматом,
содержит пустое слово тогда и только
тогда, когда его начальное состояние
одновременно является и заключительным.
,
назовем множество слов-весов всевозможных
путей в графе автомата, ведущих из
начального состояния автомата в любое
из заключительных состояний. Напомним,
что путем
в графе из одной его вершины в другую
называется последовательность дуг
(если эта последовательность пустая,
то начальная вершина пути одновременно
является и концевой вершиной), такая,
что первая дуга исходит из начальной
вершины пути, а любая из остальных – из
вершины, в которую заходит предшествующая
дуга, причем последняя дуга пути заходит
в его концевую вершину. Весом
пути назовем
слово-конкатенацию весов отдельных
дуг, образующих этот путь. Заметим, что
язык, представленный конечным автоматом,
содержит пустое слово тогда и только
тогда, когда его начальное состояние
одновременно является и заключительным.
При графическом
изображении конкретного конечного
автоматов его состояния, т.е. точки-вершины
его графа, будем метить числами из
множества
![]() ,
т.е. номерами этих состояний для данного
автомата. Необходимость в этом возникает
только при описании различных свойств
и процедур, связанных с этим автоматом.
Не ограничивая общности, можно считать,
что начальным состоянием автомата
всегда является состояние с номером 1.
Для задания графа автомата удобно
использовать матрицу переходов
,
т.е. номерами этих состояний для данного
автомата. Необходимость в этом возникает
только при описании различных свойств
и процедур, связанных с этим автоматом.
Не ограничивая общности, можно считать,
что начальным состоянием автомата
всегда является состояние с номером 1.
Для задания графа автомата удобно
использовать матрицу переходов
![]() с
с
![]() строками и
строками и
![]() столбцами, такую, что ее элемент
столбцами, такую, что ее элемент
![]() есть номер состояния, в которое ведет
дуга из
есть номер состояния, в которое ведет
дуга из
![]() -го
состояния автомата, помеченная буквой
-го
состояния автомата, помеченная буквой
![]() из алфавита
из алфавита
![]() .
Таблица описывает возможные изменения
состояния автомата при последовательной
подаче на его вход различных символов
алфавита.
.
Таблица описывает возможные изменения
состояния автомата при последовательной
подаче на его вход различных символов
алфавита.
Два автомата
![]() и
и
![]() называются эквивалентными,
если они представляют одно и то же
множество слов, т.е. если
называются эквивалентными,
если они представляют одно и то же
множество слов, т.е. если
![]()
![]() =
=
![]()
![]() .
.
Проблема
эквивалентности конечных автоматов
является разрешимой,
что подтверждается приведенным ниже
описанием алгоритма распознавания
эквивалентности двух произвольных
конечных автоматов над алфавитом
![]() .
Пусть автомат
.
Пусть автомат
![]() имеет
имеет
![]() состояний, а автомат
состояний, а автомат
![]() –
–
![]() состояний.
состояний.
Алгоритм состоит
в построении таблицы, столбцы которой
соответствуют различным буквам алфавита,
а столбцы – достижимым парам номеров
состояний этих автоматов при одновременной
подаче на их входы одних и тех же
последовательностей символов алфавита
![]() .
Начальная строка соответствует паре
.
Начальная строка соответствует паре
![]() .
В общем случае
.
В общем случае
![]() -й
элемент строки
-й
элемент строки
![]() ,
,
![]() ,
,
![]() ,
есть пара номеров состояний, соответственно,
первого и второго автоматов, в которые
они переходят из, соответственно,
,
есть пара номеров состояний, соответственно,
первого и второго автоматов, в которые
они переходят из, соответственно,
![]() -го
и
-го
и
![]() -го
состояний при подаче на входы автоматов
символа
-го
состояний при подаче на входы автоматов
символа
![]() .
Построение продолжается путем включения
новых строк для всех полученных при
построении таблицы пар, для которых
соответствующая строка еще не была
включена в таблицу. Возможны два варианта
окончания работы алгоритма построения
таблицы:
.
Построение продолжается путем включения
новых строк для всех полученных при
построении таблицы пар, для которых
соответствующая строка еще не была
включена в таблицу. Возможны два варианта
окончания работы алгоритма построения
таблицы:
-
ввиду отсутствия в ней пар, для которых еще не была построена строка значений, и
-
если при построении была получена «плохая» пара
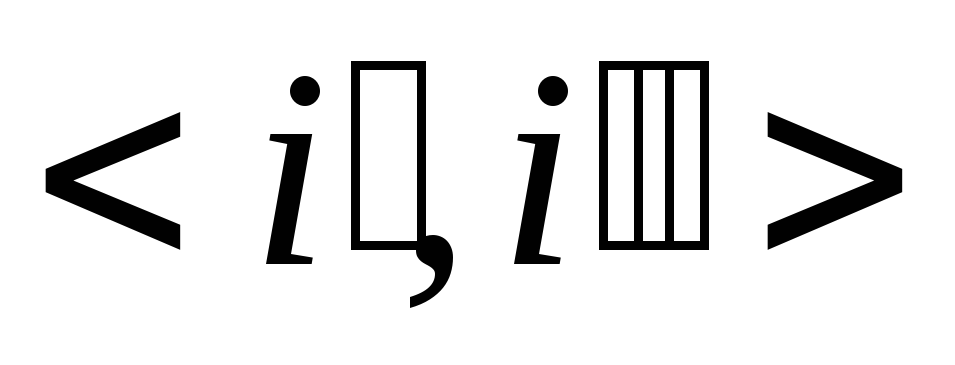 ,
такая, что
,
такая, что
 -ое
состояние является
заключительным состоянием автомата
-ое
состояние является
заключительным состоянием автомата
 ,
а
,
а
 -ое
состояние не
является
заключительным состоянием автомата
-ое
состояние не
является
заключительным состоянием автомата
 ,
или наоборот.
,
или наоборот.
В первом случае
автоматы эквивалентны (легко доказывается
индукцией по длине слов), а во втором –
нет («история» получения «плохой» пары
дает пример слова, входящего в язык,
представленный одним из автоматов, и
не входящего в язык, представленный
другим автоматом. Очевидна результативность
алгоритма – в построенной таблице не
может быть более чем
![]() строк.
строк.
На рис. 1 приведены
графические представления трех конечных
автоматов
![]() ,
,
![]() и
и
![]() над двухбуквенным алфавитом
над двухбуквенным алфавитом
![]() и построены две таблицы, первая из
которых доказывает эквивалентность
и построены две таблицы, первая из
которых доказывает эквивалентность
![]() и
и
![]() ,
а вторая – не эквивалентность
,
а вторая – не эквивалентность
![]() и
и
![]() (контрольное слово –
(контрольное слово –
![]() ).
В таблицах верхним индексом
).
В таблицах верхним индексом
![]() помечены номера заключительных состояний
в соответствующих автоматах.
помечены номера заключительных состояний
в соответствующих автоматах.
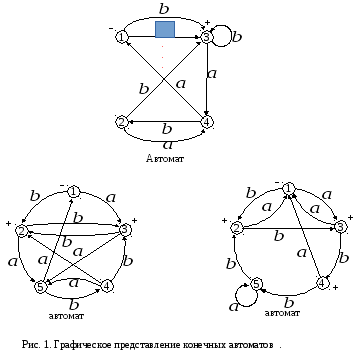
Таблица 1
-

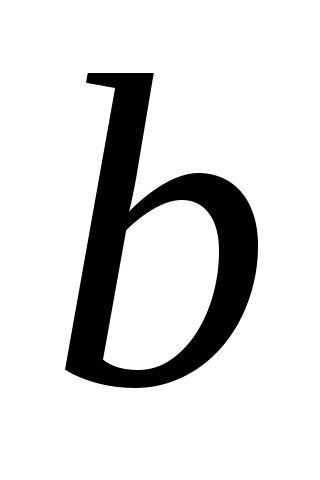
1,1
3,3
3,2
3+,3+
4,5
3,2
3+,2+
4,5
3,3
4,5
1,1
2,4
2,4
4,5
3,3
Таблица 2
-


1,1
3,3
3,2
3+,3+
4,1
3,4
3+,2+
4,1
3,3
4,1
1,3
2,2
3+,4+
4,5
3,3
1,3+
Графы переходов.
Понятие графа переходов является обобщением понятия конечного автомата, т. е. всякий конечный автомат одновременно является и графом переходов. Обобщение заключается в снятии ряда ограничений на вид ориентированного мультиграфа, задания весов дуг в графе и возможности задания не строго одной, а произвольного подмножества начальных состояний.
Граф переходов –
произвольный взвешенный ориентированный
мультиграф с множеством вершин
![]() ,
возможно, с петлями, в котором выделено
произвольное подмножество
,
возможно, с петлями, в котором выделено
произвольное подмножество
![]() начальных
вершин и
произвольное подмножество заключительных
вершин
начальных
вершин и
произвольное подмножество заключительных
вершин
![]() .
Произвольное подмножество дуг графа
помечено произвольными буквами алфавита
.
Произвольное подмножество дуг графа
помечено произвольными буквами алфавита
![]() .
.
Формальным языком
![]()
![]()
(множество слов в алфавите
(множество слов в алфавите
![]() ),
представленным
графом переходов
),
представленным
графом переходов
![]() ,
назовем множество слов-весов всевозможных
путей в графе автомата, ведущих из любой
начальной вершины графа переходов в
любую его заключительную вершину. Весом
пути назовем
слово-конкатенацию весов тех образующих
этот путь дуг, для которых задан вес. Не
ограничивая общности можно считать,
что между любыми двумя вершинами нет
нескольких дуг с одинаковыми весами.
Отметим, что в случае, когда в пути нет
дуг, имеющих вес, весом пути является
пустое слово.
,
назовем множество слов-весов всевозможных
путей в графе автомата, ведущих из любой
начальной вершины графа переходов в
любую его заключительную вершину. Весом
пути назовем
слово-конкатенацию весов тех образующих
этот путь дуг, для которых задан вес. Не
ограничивая общности можно считать,
что между любыми двумя вершинами нет
нескольких дуг с одинаковыми весами.
Отметим, что в случае, когда в пути нет
дуг, имеющих вес, весом пути является
пустое слово.
Удобной формой
задания графов переходов является
задание трех компонентов: подмножеств
![]() и
и
![]() ,
соответственно, начальных и заключительных
вершин и матрицы связей вершин размерности
,
соответственно, начальных и заключительных
вершин и матрицы связей вершин размерности
![]() (
(![]() – количество вершин в графе переходов),
элементами которой являются произвольные
подмножества букв алфавита.
– количество вершин в графе переходов),
элементами которой являются произвольные
подмножества букв алфавита.
Снятие ограничений
не приводит к расширению класса
представимых с помощью графов переходов
множеств слов по сравнению с классом
слов, представимых с помощью конечных
автоматов. Доказательство основано на
алгоритме построения (методом
подмножеств)
для любого графа переходов эквивалентного
ему конечного автомата. Алгоритм
предполагает построение матрицы с
![]() столбцами, соответствующими различным
буквам алфавита
столбцами, соответствующими различным
буквам алфавита
![]() ,
строки которой сопоставлены различным
подмножествам номеров вершин графа
переходов, которым после завершения
построения будут сопоставлены состояния
конечного автомата, эквивалентного
исходному графу переходов. Элементами
таблицы также являются подмножества
номеров вершин графа переходов, причем
построение таблицы продолжается до
тех пор, пока не будут построены строки
для всех подмножеств, полученных ранее
в качестве элементов строк. Построение
начинается с подмножества номеров
вершин, которое включает номера всех
начальных вершин графа переходов и всех
вершин, к которым есть путь из начальных
вершин, все дуги в котором не имеют
весов. Этому подмножеству будет
сопоставлено начальное состояние
искомого конечного автомата. Элемент
строки таблицы, соответствующей
некоторому подмножеству
,
строки которой сопоставлены различным
подмножествам номеров вершин графа
переходов, которым после завершения
построения будут сопоставлены состояния
конечного автомата, эквивалентного
исходному графу переходов. Элементами
таблицы также являются подмножества
номеров вершин графа переходов, причем
построение таблицы продолжается до
тех пор, пока не будут построены строки
для всех подмножеств, полученных ранее
в качестве элементов строк. Построение
начинается с подмножества номеров
вершин, которое включает номера всех
начальных вершин графа переходов и всех
вершин, к которым есть путь из начальных
вершин, все дуги в котором не имеют
весов. Этому подмножеству будет
сопоставлено начальное состояние
искомого конечного автомата. Элемент
строки таблицы, соответствующей
некоторому подмножеству
![]() номеров вершин графа переходов и букве
номеров вершин графа переходов и букве
![]() ,
определяется как подмножество номеров
тех вершин графа, к которым ведет хотя
бы одна помеченная буквой
,
определяется как подмножество номеров
тех вершин графа, к которым ведет хотя
бы одна помеченная буквой
![]() дуга из некоторой вершины
дуга из некоторой вершины
![]() и тех вершин, к которым из указанных
вершин есть путь, все дуги в котором не
имеют весов. Очевидно, что построение
таблицы всегда завершается, так как
количество различных подмножеств
номеров вершин графа переходов не может
быть больше
и тех вершин, к которым из указанных
вершин есть путь, все дуги в котором не
имеют весов. Очевидно, что построение
таблицы всегда завершается, так как
количество различных подмножеств
номеров вершин графа переходов не может
быть больше
![]() .
Полученная таблица есть не что иное,
как таблица переходов искомого конечного
автомата. Подмножество заключительных
состояний конечного автомата соответствует
тем подмножествам, в число которых
входит номер хотя бы одной заключительной
вершины исходного графа переходов.
.
Полученная таблица есть не что иное,
как таблица переходов искомого конечного
автомата. Подмножество заключительных
состояний конечного автомата соответствует
тем подмножествам, в число которых
входит номер хотя бы одной заключительной
вершины исходного графа переходов.
Эквивалентность
полученного таким образом конечного
автомата исходному графу переходов
доказывается индукцией по длине слов
в алфавите
![]() .
.
На рис. 2 приведен пример графа переходов, таблица, построенная с применением описанного алгоритма, и полученный конечный автомат.
Таким образом, мы доказали равносильность двух способов задания формальных языков – с помощью конечных автоматов и с помощью графов переходов. Теперь покажем, что класс описываемых с их помощью языков есть в точности класс регулярных языков. С этой целью опишем алгоритмы взаимной трансляции регулярных выражений и графов переходов, сохраняющей представляемых ими множеств слов.
Г раф
переходов назовем каноническим,
если он удовлетворяет следующим
требованиям:
раф
переходов назовем каноническим,
если он удовлетворяет следующим
требованиям:
-
множества начальных и заключительных вершин содержат в точности по одной вершине,
-
в начальную вершину не заходит ни одна дуга,
-
из заключительной вершины не исходит ни одна дуга.
Очевидно, что для произвольного графа переходов легко построить эквивалентный ему канонический граф. Действительно, достаточно добавить две новых вершины – из одной из них, той, которая будет единственной начальной вершиной получаемого канонического графа, построить дуги во все начальные вершины исходного графа, не приписывая им весов; во вторую, которая будет единственной заключительной вершиной получаемого канонического графа, построить дуги из всех заключительных вершин исходного графа, также не приписывания им весов. Нетрудно видеть, что требования к каноническому графу позволяют показать, что каждому пути из некоторой начальной вершины в заключительную в исходном графе взаимно однозначно соответствует путь с тем же самым весом из начальной вершины в заключительную в построенном каноническом графе. На рис. 3 схематически показано описанное преобразование.
П остроение
канонического графа переходов
остроение
канонического графа переходов
![]() ,
представляющего то же множество слов,
что и заданное регулярное выражение
,
представляющего то же множество слов,
что и заданное регулярное выражение
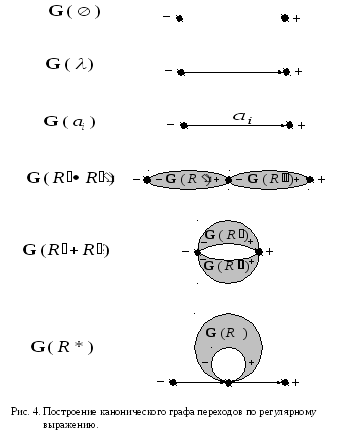
![]() ,
описано индуктивно по структуре
регулярного выражения и понятно из рис.
4, а на рис. 5 приведен пример выполнения
этого построения.
,
описано индуктивно по структуре
регулярного выражения и понятно из рис.
4, а на рис. 5 приведен пример выполнения
этого построения.
Доказательство эквивалентности исходного регулярного выражения и получаемого графа переходов для этого преобразования базируется на свойствах канонического графа переходов. Отсюда следует, что любое регулярное множество слов может быть представлено некоторым графом переходов (канонический граф переходов является частным случаем графа переходов).
Для доказательства обратного утверждения, т.е. того, что множество слов, представленное любым графом переходов, является регулярным, введем понятие обобщенного графа переходов.
 Обобщенным
каноническим
графом переходов называется конечный
ориентированный граф (обыкновенный, не
мультиграф) с одной выделенной начальной
вершиной
Обобщенным
каноническим
графом переходов называется конечный
ориентированный граф (обыкновенный, не
мультиграф) с одной выделенной начальной
вершиной
![]() ,
в которую не ведет ни одна дуга, с одной
заключительной
вершиной
,
в которую не ведет ни одна дуга, с одной
заключительной
вершиной
![]() ,
из которой не исходит ни одна дуга, и
множеством всевозможных дуг (кроме
входящих в начальную вершину и исходящих
из заключительной), взвешенных
произвольными регулярными выражениями.
,
из которой не исходит ни одна дуга, и
множеством всевозможных дуг (кроме
входящих в начальную вершину и исходящих
из заключительной), взвешенных
произвольными регулярными выражениями.
О бобщенный
граф переходов представляет
в интерпретации множество
слов, представленное регулярным
выражением, полученном объединением
по всем путям в графе из его начальной
вершины в заключительную конкатенаций
весов дуг, образующих соответствующий
путь. Очевидно, что для того, чтобы по
заданному графу переходов построить
эквивалентный ему обобщенный граф,
достаточно
бобщенный
граф переходов представляет
в интерпретации множество
слов, представленное регулярным
выражением, полученном объединением
по всем путям в графе из его начальной
вершины в заключительную конкатенаций
весов дуг, образующих соответствующий
путь. Очевидно, что для того, чтобы по
заданному графу переходов построить
эквивалентный ему обобщенный граф,
достаточно
-
для всех помеченных дуг исходного графа рассматривать их веса (буквы алфавита) как регулярные выражения,
-
для всех непомеченных дуг исходного графа считать их весом
 ,
, -
для кратных дуг между вершинами исходного графа заменить их на единственную дугу с весом – объединением весов этих дуг,
-
для всех упорядоченных пар вершин
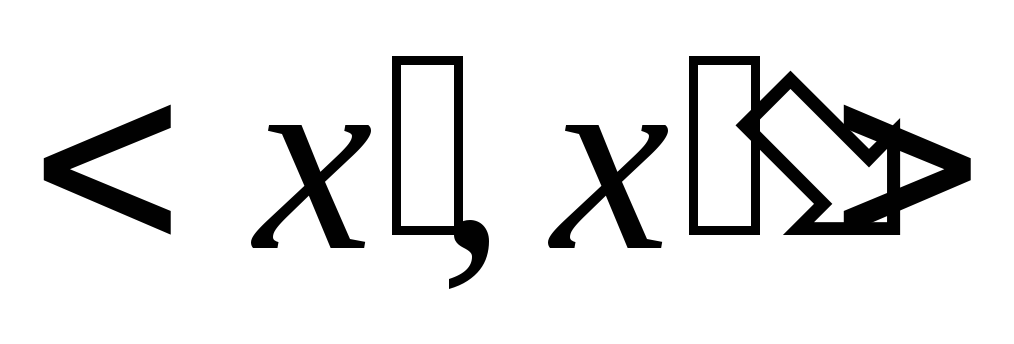 ,
,
 ,
, между которыми в исходном графе не
было дуг, ввести дугу с весом
,
, между которыми в исходном графе не
было дуг, ввести дугу с весом
 .
.
Т еорема.
Класс множеств слов, представимых
графами переходов, есть класс регулярных
множеств слов.
еорема.
Класс множеств слов, представимых
графами переходов, есть класс регулярных
множеств слов.
Доказательство заключается в построении регулярного выражения, эквивалентного в интерпретации заданному графу переходов. Пусть задан произвольный граф переходов. Преобразуем его к виду эквивалентного ему обобщенного графа переходов. К полученному обобщенному графу переходов можно применить метод последовательного исключения всех вершин, кроме начальной и заключительной, сохраняющий множество слов, представляемое полученными на каждом шаге обобщенными графами переходов.
Р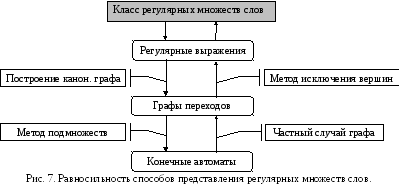 ис.
6 поясняет выполнение одного шага
применения этого метода, связанного с
исключением
ис.
6 поясняет выполнение одного шага
применения этого метода, связанного с
исключением
![]() -й
внутренней вершины обощенного графа
переходов. Очевидно, что вес единственной
остающейся в результате дуги
-й
внутренней вершины обощенного графа
переходов. Очевидно, что вес единственной
остающейся в результате дуги
![]() и есть искомое регулярное выражение.
и есть искомое регулярное выражение.
Выводы. Все рассмотренные формальные понятия – регулярные выражения, конечные автоматы и графы переходов – являются равносильными способами задания класса регулярных множеств слов в заданном алфавите (рис. 7).
